Основная часть
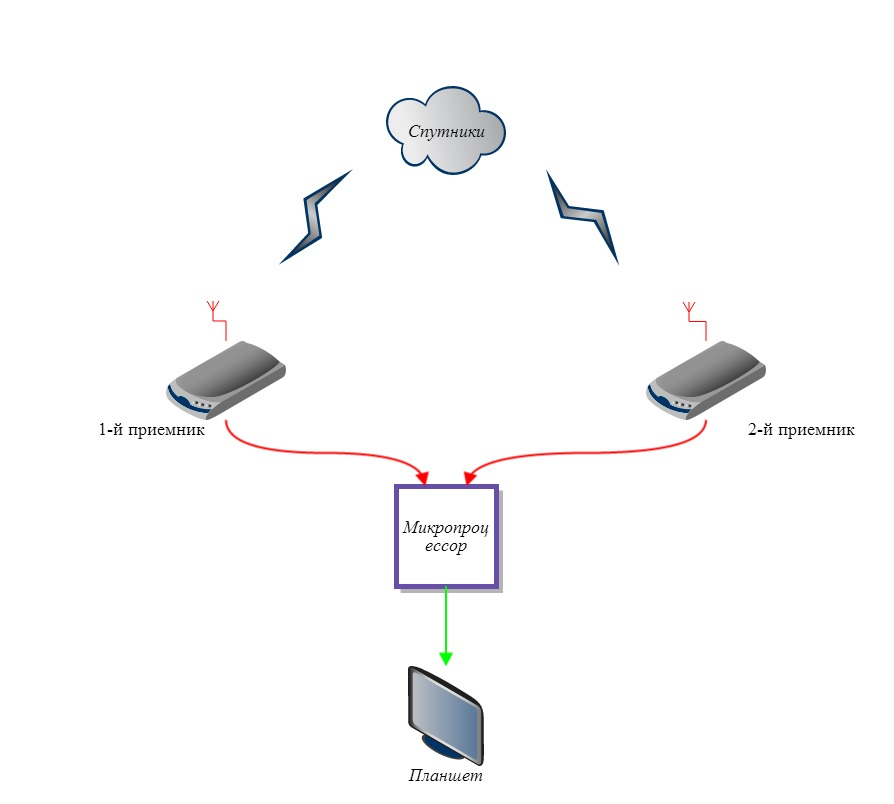
В моем дипломном проекте координаты, получаемые приемниками, подаются на микропроцессор, а дальше к планшету, на котором будет установлена программа для определения стороны, в которую направлено устройство.
В основе работы системы GPS лежит:
1) спутниковая трилатерация (на ней базируется работа системы);
2) спутниковая дальнометрия (измерение расстояний до спутников);
3) точная временная привязка (высокоточная синхронизация отсчета времени в системе спутники-приемники);
4) точное положение спутников в космосе;
5) коррекция ошибок, вносимых задержкой радиосигнала спутника в ионосфере и тропосфере.
Спутниковая трилатерация предполагает, что точные координаты любой точки на поверхности Земли могут быть вычислены путем измерений расстояний от группы спутников, если их положение в космосе известно. В этом случае спутники являются пунктами с известными координатами. Предположим, что расстояние от одного спутника известно, и вокруг него можно описать сферу заданного радиуса. Если известно также расстояние до второго спутника, то определяемое местоположение будет расположено где-то в круге, задаваемом пересечением двух сфер. Третий спутник определяет две точки на окружности. Четвертый спутник позволяет окончательно точно определить местоположение точки. Таким образом расстояние, зная расстояние до четырех спутников, можно вычислить координаты определяемой точки (рис. 1.1).
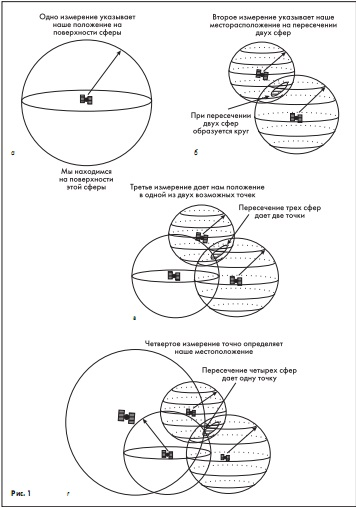
Рисунок 1.1
Расстояние до спутников определяется по измерениям времени прохождения радиосигнала от космического аппарата до преемника, умноженным на скорость света. Для того чтобы определить время распространения сигнала, нам необходимо знать, когда он был передан со спутника. Для этого на спутнике и в приемнике одновременно генерируется одинаковый псевдослучайный код. Каждый спутник системы GPS передает два радиосигнала: на частоте L!=1575,42 МГц и L2=1227,60 МГц. Сигнал L1 имеет два дальномерных кода с псевдослучайным шумом (PRN), P-код и C/A код. «Точный», или P–код, может быть зашифрован для военных целей. «Грубый», или C/A-код, не зашифрован. Сигнал частоты L2 модулируется только с P-кодом.
Большинство гражданских пользователей при работе с GPS-системами используют C/A-код. Некоторые приемники Trimble, применяемые в геодезии, работают с P-кодом. Приемник проверяет входящий сигнал со спутника и определяет, когда он сам генерировал такой же код. Полученная разница, умноженная на скорость света, и дает искомое расстояние. Использование кода позволяет приемнику определить временную задержку в любое время. Кроме того, спутники могут излучать сигнал на одной и той же частоте, так как каждый спутник идентифицируется по своему PRN.
Как видно из вышесказанного, вычисления напрямую зависят от точности хода часов на спутниках и в приемниках. Код должен генерироваться на спутнике и в приемнике строго в одно и то же время. На спутниках установлены атомные часы, имеющие точность около одной наносекунды. Однако это решение является слишком дорогим, чтобы использовать его в приемниках GPS. Поэтому для устранения ошибок хода часов приемника используются результаты измерения сигналов от четвертого спутника. Их можно использовать для устранения ошибок, которые возникают, если часы на спутнике и в приемники
не синхронизированы. Рисунок 1.2 наглядно это показывает.
24 рабочих спутника сиcтемы Navstar расположены на высоте примерно 20 200 км от поверхности Земли с орбитальным периодом в 12 часов. В шести различных плоскостях имеющих наклон к экватору в 55°, расположено по 4 спутника. Указанная высота необходима для обеспечения стабильности орбитального движения спутников и уменьшения фактора влияния атмосферы.
Некоторые источники ошибок, возникающих при работе GPS, являются трудноустранимыми. Вычисления предполагают, что сигнал распространяется с непрерывной скоростью, которая равна скорости света. Однако на практике все обстоит гораздо сложнее. Скорость света является константой только в вакууме. Когда сигнал проходит через ионосферу и тропосферу, скорость его распространения уменьшается, что приводит к ошибкам в измерении дальности.
В современных GPS-приемниках используют всевозможные алгоритмы устранения этих задержек. Иногда возникают ошибки хода атомных часов и отклонения орбит спутников, но они обычно незначительны и тщательно отслеживаются станциями слежения. Многолучевая интерференция также вносит ошибки в определение местоположения с помощью GPS. Это происходит, когда сигнал отражается от объектов, расположенных на земной поверхности, что создает заметную интерференцию с сигналами, приходящими непосредственно со спутников. Специальная техника обработки сигнала и продуманная конструкция антенн позволяет свести к минимуму этот источник ошибок.
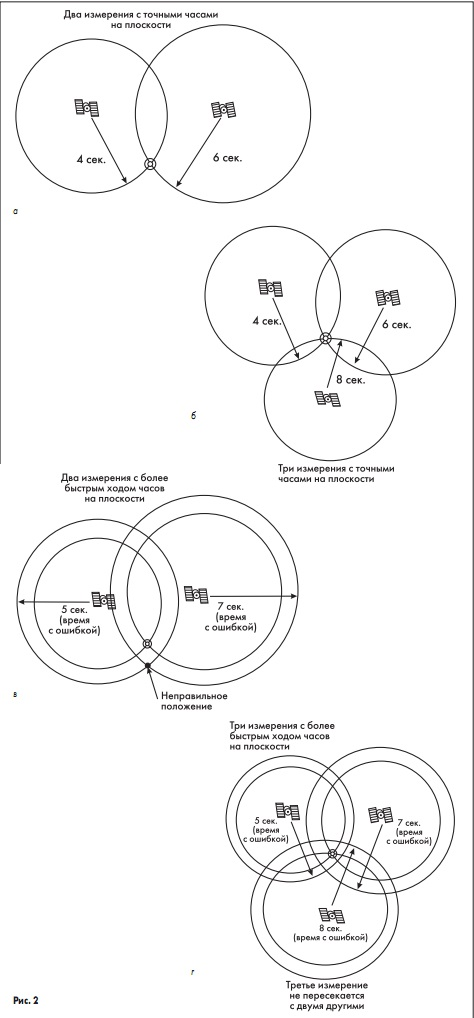
Рисунок 1.2
Процесс определения координат при нахождении на одном месте ил при перемещении сводится к получению сигналов со спутников системы GPS, их анализу и вычислению данных о местоположении приемника. Результаты вычислений отображаются в виде координат на дисплее приемника (рис.3).
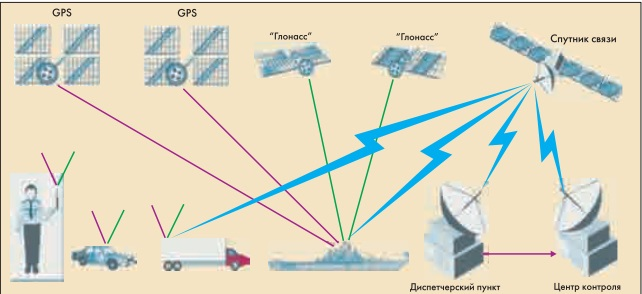 Рисунок 3. Структура сети GPS/ГЛОНАСС
Рисунок 3. Структура сети GPS/ГЛОНАСС
Приемники GPS обладают способностью вычислять скорость и направление движения, могут обеспечить привязку к загружаемой в приемник или портативный компьютер карте местности или карте крупного города. Это свойство имеет огромную практическую способность, так как позволяет легко ориентироваться в незнакомой местности и наблюдать свое перемещение на экране монитора.
У приемников GPS имеются накопитель данных, предназначенный для хранения измеренных координат, а программное обеспечение контролирует установки интервала измерений и количества хранимых GPS-данных. Накопитель, в зависимости от назначения приемника, может быть либо выполнен в виде отдельного устройства, либо интегрирован с приемником в одном корпусе.
Каждый спутник GPS излучает на двух частотах – L1 и L2 – специальный навигационный сигнал в виде псевдослучайной фазоманипулированной последовательности, в котором зашифрованы два вида кода – код C/A (coarse/acquisition clear/acquisition), или «грубый» код, доступный широкому кругу гражданских потребителей и позволяющий получать лишь приблизительную оценку местоположения, и код P (precision code), обеспечивающий более точное вычисление координат. Первоначально пользование кодом P было ограничено, но 1 мая 2000 г. эти ограничения распоряжением президента США были сняты, что позволило значительно увеличить точность этих приемников без необходимости их модернизации.
Код C/A передается по частоте L1 с использованием фазовой манипуляции псевдослучайной последовательности длиной 1023 символа с зашитой от ошибок. Период повторения C/A кода – 1мс. Тактовая частота – 1,023 МГц. Код P передается на частоте L2 с применением сверхдлинной псевдослучайной последовательности с периодом повторения 267 дней. Тактовая частота – 10,23 МГц. Кроме этих кодов в сигнале GPS может присутствовать и код Y, представляющий собой шифрованную версию кода P.
Кроме кодов C/A и P спутник GPS регулярно передает специальное сообщение, содержащее дополнительные сведения. Пользователь получает информацию о системном времени, эфемеридах (наборах параметров, точно описывающих орбиту движения спутника), прогнозе ионосферной задержки, показателях работоспособности. Передача навигационного сообщения длиной 1500 бит осуществляется со скоростью 50 бит/с на частотах L1 и/или L2.
Рисунок 1 – Основная блок-схема алгоритма определения координат
На рис. 1 показана основная блок-схема, наглядно иллюстрирующая алгоритм работы приемника по определению координат потребителя, начиная с включения приемника и заканчивая нахождением оценки координат потребителя. Первичная обработка сигнала производится для каждого из видимых спутников, а во время вторичной обработки до каждого спутника высчитывается псевдодальность по коду и фазе; зная эти расстояния, вычисляют местоположение приемника.
Рисунок 2 - Блок-схема первичной обработки сигнала
Спутники GPS передают сигналы на двух частотах: 1575, 42 МГц и 1227, 60 МГц. На вход приемника поступают сигналы от спутников, находящихся в зоне радиовидимости. Так как для решения навигационной задачи необходимо измерить псевдодальности относительно, как минимум, четырех спутников, то приемник должен быть многоканальным (от 4 до 12 каналов).
После включения питания и начального тестирования навигационная аппаратура потребителей (НАП) входит в режим поиска сигнала навигационных спутников. Суть алгоритма поиска заключается в последовательном переборе всех возможных значений доплеровского смещения частоты при фиксированном значении битов генератора псевдослучайной последовательности (ПСП), в общем случае уникальной для каждого спутника. Для ускорения этого процесса в навигационных системах GPS используется информация долгосрочного прогноза положения спутников, которая называется альманахом.
Спецчасть
Математическая модель
Здесь мы даем математическую модель оценки позиции.
Постановка задачи. Заданы два одночастотных GPS приемника, которые именуются базовым (БС) s и мобильным (МБ) r, находящиеся на поверхности Земли, расположенные на относительно небольшом расстоянии друг от друга (не более 10 км.). Мы хотим найти вектор базовой линии x, т.е. вектор, направленный от приемника s к приемнику r. По базовой линии однозначно определяются координаты мобильного приемника. Оба приемника постоянно принимают сигналы с некоторого множества спутников GPS. Это множество «видимых» с обоих приемников спутников с течением времени меняется: спутники GPS все время покидают и заходят в «зону видимости».
Координаты базового приемника статичны и считаются известными в международной системе ECEF с достаточно высокой точностью (1-2 мм.). В режиме постобработки координаты мобильного приемника считаются также неизменными в определенный промежуток времени, в которое проводятся измерения.
Каждый из приемников способен высчитывать и выдавать свои измерения расстояния до заданного спутника в определенный момент времени (именуемый эпохой). Причем эти расстояния измеряются аппаратной частью приемника двумя способами: кодовым и фазовым. В данной работе описывается алгоритм решения навигационной задачи посредством кодовых и фазовых измерений. В грубом приближении, расстояние от приемника до спутника по коду рассчитывается как время запаздывания сигнала относительно системного отсчета времени, помноженная на скорость света (берется как скорость сигнала). А дальность по фазе определяется как количество длин волн несущей сигнала, которые помещаются на отрезке между спутником и приемником, помноженное на длину волны сигнала.
Цель задачи: определить координаты мобильного приемника в режиме постобработки, то есть для случая когда в качестве входных данных численного метода используются измерения, получаемые как до так и после эпохи, в которое нужно определить искомые координаты мобильного приемника.
| Базовая станция s |
| Мобильная станция станция r |
| Вектор x |
| x/2 |
| x/2 |
| ei |
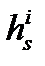
|
| i -й НКА |
Рисунок 1 - Геометрическое расположение БС, МС и НКА
Пусть в некоторую эпоху 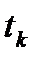 в поле зрения базовой станции находятся множество {d} спутников, а мобильной станции некоторое множество {f} спутников. Пересечение множеств {d} и {f} как раз таки является множеством спутников, с которыми будет происходить работа по дифференциальной коррекции. Обозначим это множество {m} (в количестве m), которое обычно называется рабочим созвездием из навигационных космических аппаратов (НКА).
в поле зрения базовой станции находятся множество {d} спутников, а мобильной станции некоторое множество {f} спутников. Пересечение множеств {d} и {f} как раз таки является множеством спутников, с которыми будет происходить работа по дифференциальной коррекции. Обозначим это множество {m} (в количестве m), которое обычно называется рабочим созвездием из навигационных космических аппаратов (НКА).
Нам необходимы следующие переменные для описания геометрии относительного положения спутников и GPS приемников (рисунок 1):
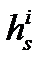 - вектор, направленный от БС s к i -му НКА;
- вектор, направленный от БС s к i -му НКА;
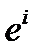 - единичный вектор, направленный из середины базовой линии x к i -му НКА;
- единичный вектор, направленный из середины базовой линии x к i -му НКА;
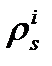 - дальность в длинах волн от БС до i -го НКА;
- дальность в длинах волн от БС до i -го НКА;
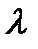 - длина волны (для частоты L1, используемой здесь, l »19 см)
- длина волны (для частоты L1, используемой здесь, l »19 см)
Верхний индекс определяет спутник, нижний индекс определяет приемник. После того, как введем обозначение:
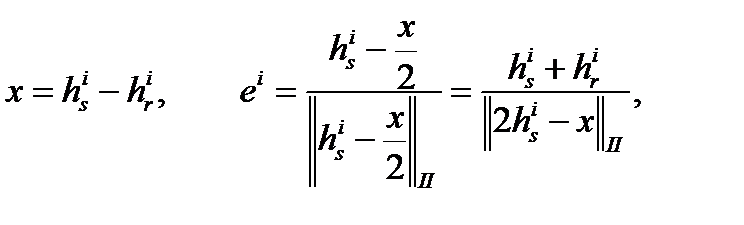
получим что:
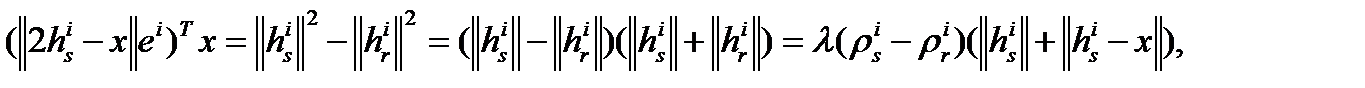
дающее:
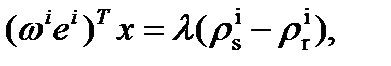 (2.1) (2.1)
|
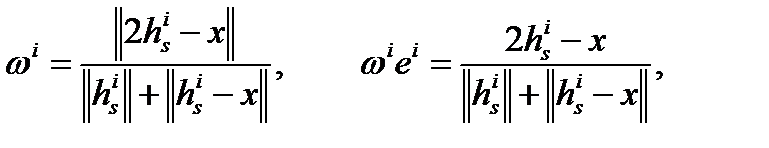 (2.2) (2.2)
|
Заметим, что 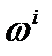 примерно равно 1, то есть вектора, направленные от приемников БС и МС к одному и тому же спутнику почти что коллинеарны, и мы можем заменить этот параметр на 1 для приложений, в которых нет необходимости производить высокоточное определение местоположения. Но для некоторых высокоточных GPS приложений нам может понадобиться неединичный параметр
примерно равно 1, то есть вектора, направленные от приемников БС и МС к одному и тому же спутнику почти что коллинеарны, и мы можем заменить этот параметр на 1 для приложений, в которых нет необходимости производить высокоточное определение местоположения. Но для некоторых высокоточных GPS приложений нам может понадобиться неединичный параметр 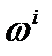 . Данная математическая модель позволяет делать такое упрощение, потому что в дальнейшем, в разделе 4, показано каким образом производится перерасчет x c учетом этого упрощения.
. Данная математическая модель позволяет делать такое упрощение, потому что в дальнейшем, в разделе 4, показано каким образом производится перерасчет x c учетом этого упрощения.
Предположим, что сигнал от i -го спутника приходит на приемник s в момент времени 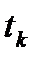 и он доходит от спутника до получения его приемником за период времени
и он доходит от спутника до получения его приемником за период времени 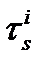 . В момент времени
. В момент времени 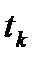 измеряется фаза несущей
измеряется фаза несущей 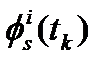 (в длинах волн) и измеряется код
(в длинах волн) и измеряется код 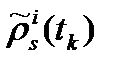 (также в длинах волн) от приемника s до i -го спутника (см. [14, раздел 5.2.2] или [15, раздел 3.4]).
(также в длинах волн) от приемника s до i -го спутника (см. [14, раздел 5.2.2] или [15, раздел 3.4]).
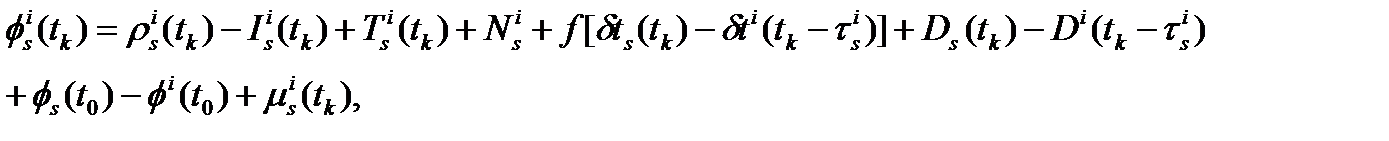 (2.3) (2.3)
|
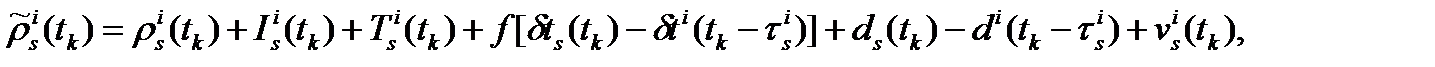 (2.4) (2.4)
|
где размерности каждого из выше приведенных уравнений определяются как “количество длин волн”,
- 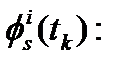 измерение фазы несущей в момент времени
измерение фазы несущей в момент времени 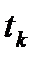 .
.
- 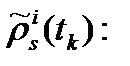 измерение кода в момент времени
измерение кода в момент времени 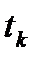 .
.
- 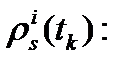 измеренное расстояние между приемником s БС в момент времени
измеренное расстояние между приемником s БС в момент времени 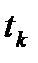 и i -м НКА в момент времени
и i -м НКА в момент времени 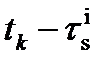 .
.
- 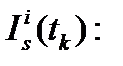 ионосферная ошибка, вносимая в дальность, в момент времени
ионосферная ошибка, вносимая в дальность, в момент времени 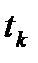 .
.
- 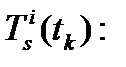 тропосферная ошибка, вносимая в дальность, в момент времени
тропосферная ошибка, вносимая в дальность, в момент времени 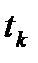 .
.
- 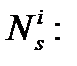 целочисленная неопределенность.
целочисленная неопределенность.
- 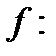 частота несущей L1;
частота несущей L1;
- 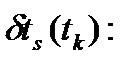 ошибка часов приемника в момент времени
ошибка часов приемника в момент времени 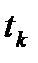 ;
;
- 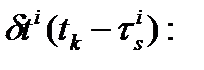 ошибка часов НКА в момент времени
ошибка часов НКА в момент времени 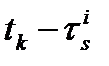 ;
;
- 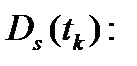 задержки в аппаратуре приемника при измерениях фазы несущей в момент времени
задержки в аппаратуре приемника при измерениях фазы несущей в момент времени 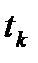 .
.
- 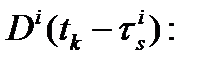 задержки в аппаратуре НКА при измерениях фазы несущей в момент времени
задержки в аппаратуре НКА при измерениях фазы несущей в момент времени 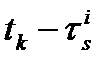 .
.
- 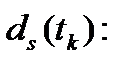 задержки в аппаратуре приемника при измерениях кода в момент времени
задержки в аппаратуре приемника при измерениях кода в момент времени 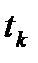 .
.
- 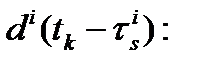 задержки в аппаратуре НКА при измерениях кода в момент времени
задержки в аппаратуре НКА при измерениях кода в момент времени 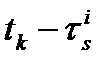 .
.
- 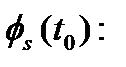 начальная фаза генератора сигнала несущей приемника в начальное время
начальная фаза генератора сигнала несущей приемника в начальное время 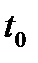 .
.
- 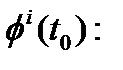 начальная фаза генератора сигнала несущей передатчика НКА в начальное время
начальная фаза генератора сигнала несущей передатчика НКА в начальное время 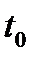 .
.
- 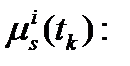 шум измерений фазы несущей, включая ошибки переотражения, в момент времени
шум измерений фазы несущей, включая ошибки переотражения, в момент времени 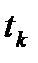 .
.
- 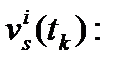 шум измерений кода, включая ошибки переотражения, в момент времени
шум измерений кода, включая ошибки переотражения, в момент времени 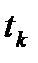 .
.
Ионосферная ошибка 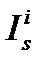 , тропосферная ошибка
, тропосферная ошибка 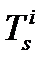 и ошибка часов НКА может быть промоделирована [11, раздел 4.4 и 5.3]. В разделе 4 мы рассмотрим численно реализованные нами тропосферную и ионосферную модели для учете данных ошибок.
и ошибка часов НКА может быть промоделирована [11, раздел 4.4 и 5.3]. В разделе 4 мы рассмотрим численно реализованные нами тропосферную и ионосферную модели для учете данных ошибок.
Вычтем уравнение измерения фазы несущей, соответствующее приемнику r, из (2.3) и замечая, что величина:
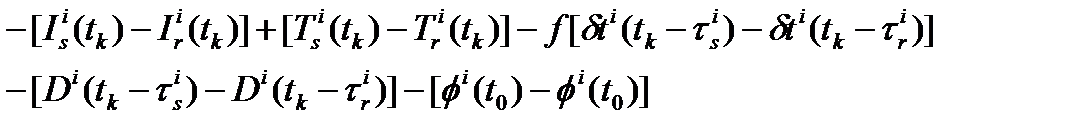
будет незначительна для коротких базовых линий, мы получим уравнения первых фазовых разностей:
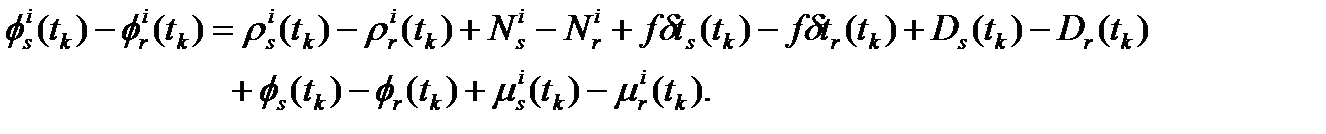 (2.5) (2.5)
|
Для уменьшения числа зависимых неизвестных, мы можем просто объединить ошибки часов приемника, задержки в аппаратуре приемника, и начальные фазы сгенерированных несущих сигналов вместе. Заметив, что приемник s и r встречаются в каждом уравнении, мы можем пропустить эти индексы и обозначить эпоху времени k нижним индексом k. Таким образом, определяя:
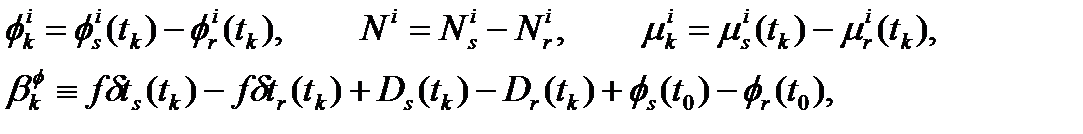
из (2.5) и (2.1) получим что:
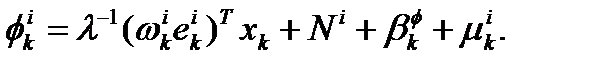 (2.6) (2.6)
|
Аналогично, введя обозначения:
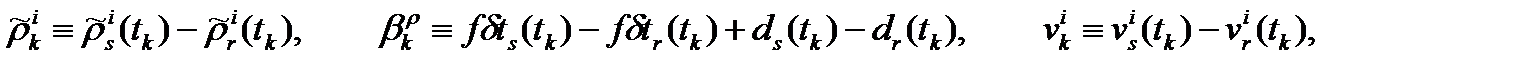
мы получим из (4) уравнения первых кодовых разностей:
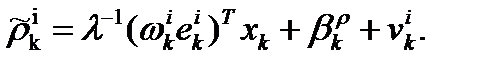 (2.7) (2.7)
|
Следуя литературе [15, раздел 3.4]), мы положим, что все 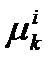 в уравнениях измерений фазы несущей (и все
в уравнениях измерений фазы несущей (и все 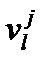 в уравнениях кодовых измерений) для различных НКА и различных эпох есть некоррелированные шумы с нормальным распределением, следовательно эти
в уравнениях кодовых измерений) для различных НКА и различных эпох есть некоррелированные шумы с нормальным распределением, следовательно эти 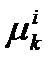 и
и 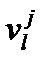 независимы. Введем:
независимы. Введем:
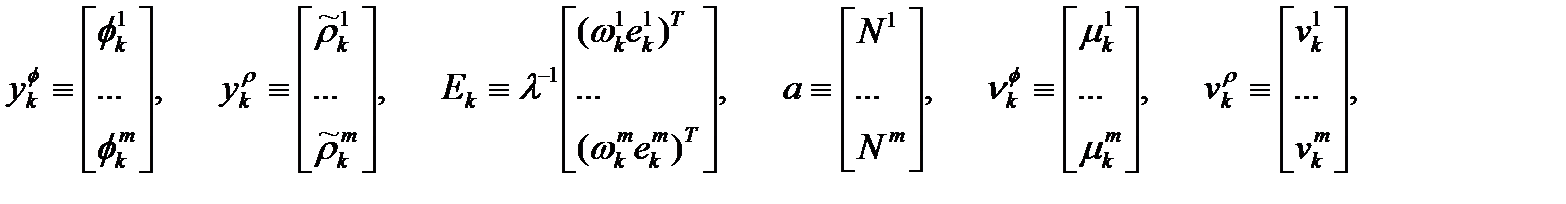
|
мы получим (помня, что 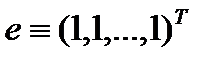 ) из (2.6) и (2.7):
) из (2.6) и (2.7):
 (2.8) (2.8)
| |
 (2.9) (2.9)
|
где мы полагаем, что среднеквадратические отклонения 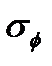 и
и 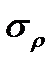 являются известными. Уравнения (2.8) и (2.9) являются желаемыми (искомыми) уравнениями первых разностей в эпоху k.
являются известными. Уравнения (2.8) и (2.9) являются желаемыми (искомыми) уравнениями первых разностей в эпоху k.
Численный метод
В общем случае, для решения системы линейных уравнений (2.8), (2.9) применяется метод наименьших квадратов, но для повышения вычислительной эффективности и устойчивости алгоритма, используют разноплановые модификации данного метода.
Для решения общей линейной проблемы наименьших квадратов, имеется два основных метода: метод нормальных уравнений и метод QR факторизации (в которой заложены ортогональные преобразования). Плохая обусловленность матрицы коэффициентов (что может быть следствием плохой геометрии расположения НКА GPS) может привести к увеличению вычислительных погрешностей метода. Поэтому, для того чтобы не увеличивать коррелированность входной системы уравнений и повысить численную устойчивость алгоритма, вместо простых вторых разностей в методе используются ортогональные вторые разности [5, раздел 5.3].
Следуя [3], мы распишем рекурсивный алгоритм ортогональных преобразований для оценки позиции, основанный на уравнениях (2.8) и (2.9) измерений первых разностей фазы несущей и кода. Мы собираемся полностью использовать структуру задачи (для примера, учтем факт того, что вектор целочисленных неопределенностей идентичен на каждом шаге при отсутствии срывов циклов или при уходе или заходе НКА GPS в рабочее созвездие) для того, чтобы сделать алгоритм как можно более эффективным. Отметим, что Тибериус [15] также использует рекурсивный алгоритм. Но он использует стандартный подход SRIF, основанный на уравнениях измерений вторых разностей фазы несущей и/или кода.
На настоящий момент времени мы предполагаем, что 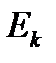 в (2.8) и (2.9) известны, и что число видимых НКА не изменяется во временной промежуток наблюдения. Сначала мы устраним
в (2.8) и (2.9) известны, и что число видимых НКА не изменяется во временной промежуток наблюдения. Сначала мы устраним 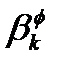 из уравнения (2.8) измерений фазы несущей.
из уравнения (2.8) измерений фазы несущей.
Пусть 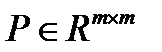 есть преобразование Хаусхолдера (смотрите также [5, стр. 209]) такое, что:
есть преобразование Хаусхолдера (смотрите также [5, стр. 209]) такое, что:
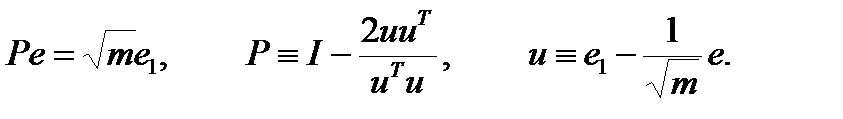 (2.10) (2.10)
|
Отметим, что матрица 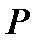 симметричная и ортогональная. Представим
симметричная и ортогональная. Представим 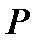 как
как 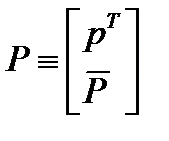 , тогда:
, тогда:
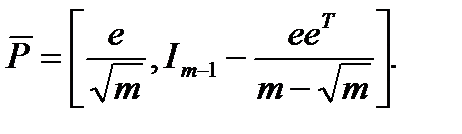 (2.11) (2.11)
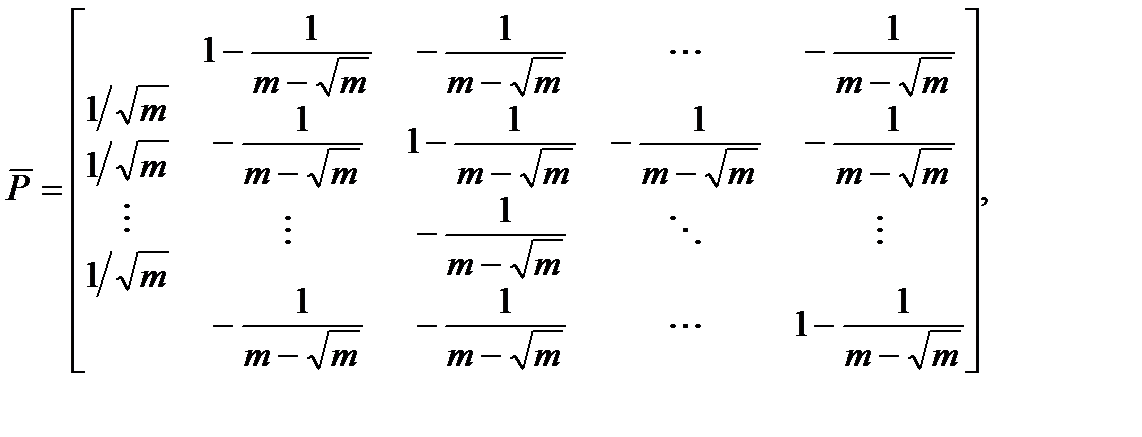 где
где 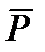 имеет размерность {m, m-1}. имеет размерность {m, m-1}.
|
Умножая (2.9) на 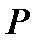 слева, получим:
слева, получим:
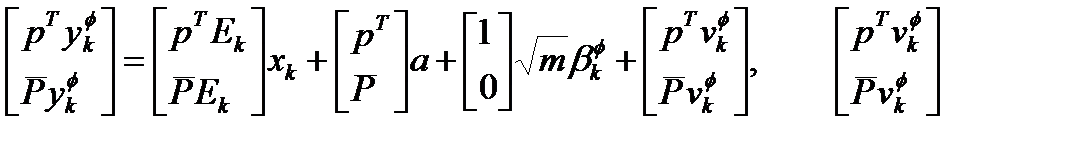 ~ ~ 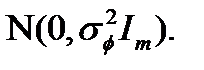 (2.12) (2.12)
|
Так как верхнее уравнение в (2.12) включает неизвестное (и не желательное) выражение 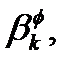 его можно исключить из алгоритма оценки положения мобильной станций. Таким образом, мы имеем:
его можно исключить из алгоритма оценки положения мобильной станций. Таким образом, мы имеем:
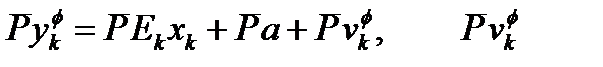 ~ ~ 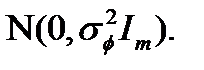 (2.13) (2.13)
|
Заметим, что мы использовали простое преобразование Хаусхолдера, вместо часто используемой техники двойных разностей для устранения неизвестной переменной 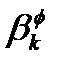 . Его главным преимуществом является то, что преобразованные измерения являются все еще некоррелированными. Техника ортонормализации Грама-Шмидта, которая может также устранить
. Его главным преимуществом является то, что преобразованные измерения являются все еще некоррелированными. Техника ортонормализации Грама-Шмидта, которая может также устранить 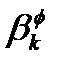 и сделать инструмент трансформации некоррелированным, не является таким прямым, как техника преобразования Хаусхолдера.
и сделать инструмент трансформации некоррелированным, не является таким прямым, как техника преобразования Хаусхолдера.
Так как 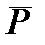 является матрицей
является матрицей 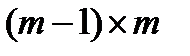 , она не имеет полного ранга по столбцу и мы не в состоянии получить однозначную оценку
, она не имеет полного ранга по столбцу и мы не в состоянии получить однозначную оценку 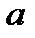 . Если мы положим
. Если мы положим 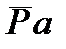 как новый вектор, то мы потеряли бы целое натуральное
как новый вектор, то мы потеряли бы целое натуральное 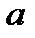 . Поэтому, идем другим путем и введем вектор
. Поэтому, идем другим путем и введем вектор 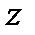 двойных разностей целочисленных неопределенностей (double difference integer ambiguity - DDIA)
двойных разностей целочисленных неопределенностей (double difference integer ambiguity - DDIA)
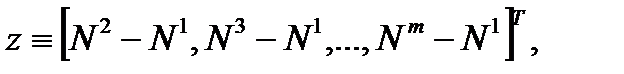 (2.14) (2.14)
|
где без потери общности мы выбрали первый попавшийся НКА как «референсный» и присвоили ему номер 1. Заметим, что 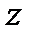 все еще вектор целых чисел. Определим:
все еще вектор целых чисел. Определим:
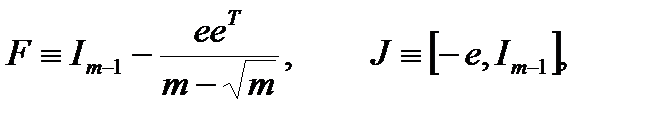 (2.15) (2.15)
|
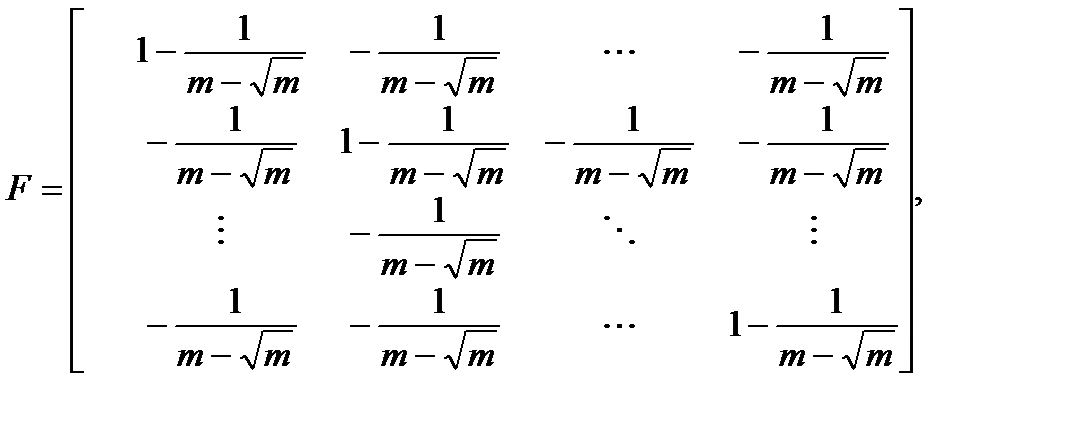
где 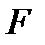 несингулярная квадратная матрица размерности {m-1} и
несингулярная квадратная матрица размерности {m-1} и 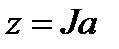 . Это легко проверить, используя (2.12)
. Это легко проверить, используя (2.12)
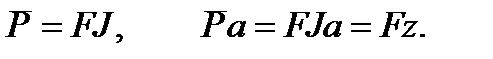
| ((2.17) |
Таким образом, выражение (2.14) может быть переписано как:
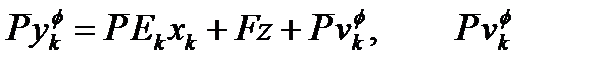 ~ ~ 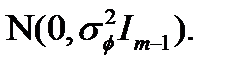
| ((2.18) |
Подобным образом мы можем также устранить 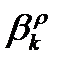 из уравнения (10) измерений кода и при этом получим:
из уравнения (10) измерений кода и при этом получим:
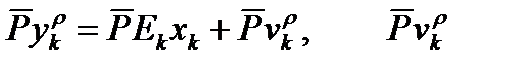 ~ ~ 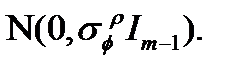
| ((2.19) |
Для того чтобы при объединении 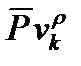 и
и 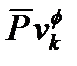 получившийся параметр имел такую же ковариационную матрицу как
получившийся параметр имел такую же ковариационную матрицу как 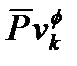 , мы определим
, мы определим  и умножим (2.19) на
и умножим (2.19) на  , а затем объединим результирующее уравнение и (2.18):
, а затем объединим результирующее уравнение и (2.18):
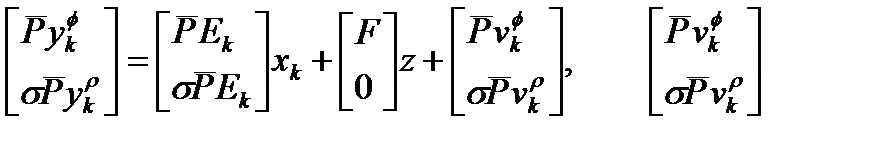 ~ ~ 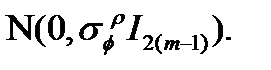
| ((2.20) |
Последний член в уравнений (2.20), 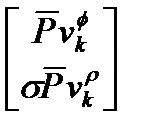 , по своей сути является неоднородностью в системе линейных уравнений, неточностью, вызванная шумами и переотражениями. Эта неоднородность подчиняется нормальному распределению, то есть, ее пределы изменения значений могут быть оценены, опираясь на результаты ограниченного количества экспериментов с дифференциальной системой. Как показывает практика, данный вид погрешностей на порядок ниже погрешностей, возникающих из-за атмосферной задержки. Поэтому, для упрощения дальнейшего математического анализа, опустим эту неоднородность из уравнения.
, по своей сути является неоднородностью в системе линейных уравнений, неточностью, вызванная шумами и переотражениями. Эта неоднородность подчиняется нормальному распределению, то есть, ее пределы изменения значений могут быть оценены, опираясь на результаты ограниченного количества экспериментов с дифференциальной системой. Как показывает практика, данный вид погрешностей на порядок ниже погрешностей, возникающих из-за атмосферной задержки. Поэтому, для упрощения дальнейшего математического анализа, опустим эту неоднородность из уравнения.
Теперь приведем уравнение (2.20) к виду, пригодному для численной реализации. Правую часть (2.20) можно переписать как
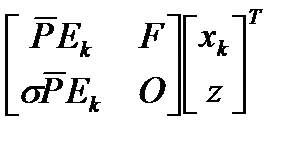 ,
,
где O – квадратичная матрица, состоящая из нулей, размерности {m-1}.
Таким образом, система уравнений (2.20) может быть записана в следующей матричной форме:
| Aс = B, (2.21) |
где
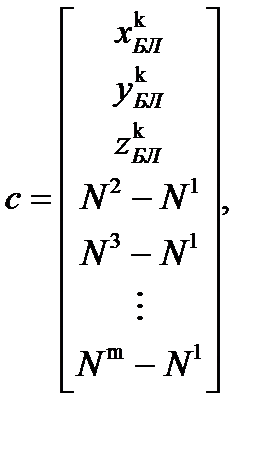
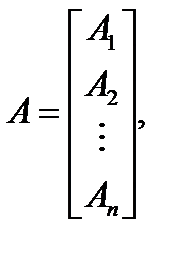
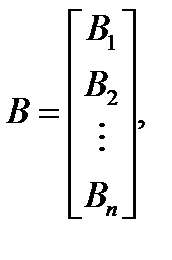
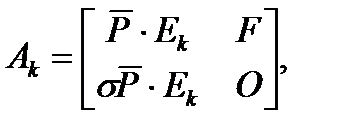
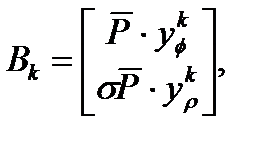
где k проходит целые числа от 1 до n включительно.
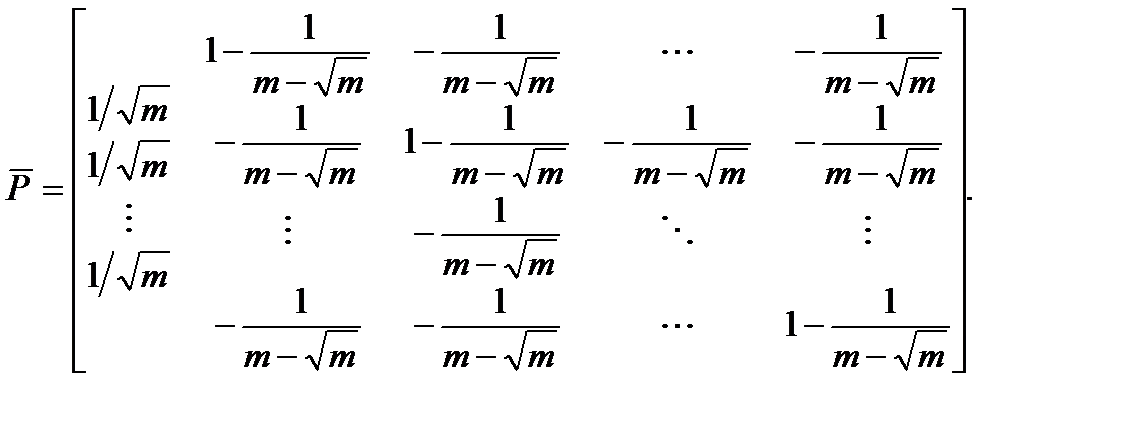
Матрица 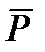 имеет размерность {m, m-1}.
имеет размерность {m, m-1}.
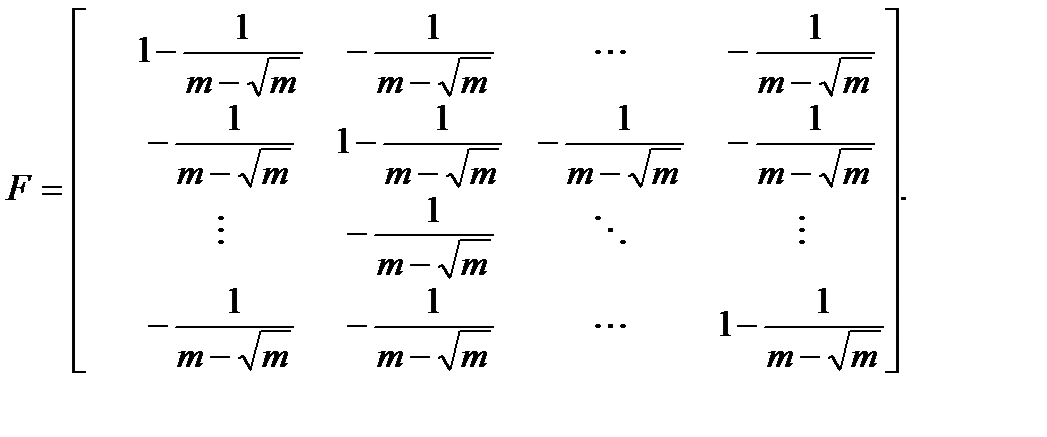
Матрица F имеет размерность {m-1, m-1}.
Обозначения:
n – количество эпох, в которые производятся наблюдения;
m – количество спутников в рабочем созвездий;
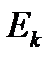 - матрица, составленная из единичных векторов, поделенных на длину волны L1 и коллинеарных направлению на спутники в эпоху с номером k (эпохой в литературе по СНС называется момент времени, в который производится измерение);
- матрица, составленная из единичных векторов, поделенных на длину волны L1 и коллинеарных направлению на спутники в эпоху с номером k (эпохой в литературе по СНС называется момент времени, в который производится измерение);
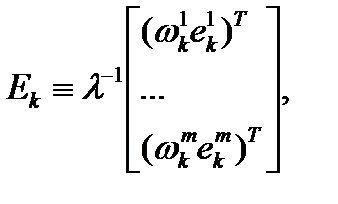
где 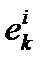 - единичный вектор, направленный из середины базовой линии
- единичный вектор, направленный из середины базовой линии 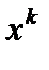 к i -му НКА в эпоху
к i -му НКА в эпоху 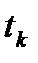 ;
;
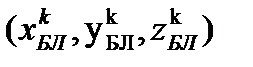 – координаты вектора, соединяющего базовый и мобильный приемники, то есть вектора базовой линии в эпоху
– координаты вектора, соединяющего базовый и мобильный приемники, то есть вектора базовой линии в эпоху 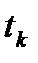 ;
;
Переопределенная система (2.21) решается методом наименьших квадратов (ищется с, минимизирующая эвклидову норму 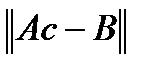 ) приведением матрицы
) приведением матрицы 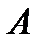 к верхнетреугольной форме методом Хаусхолдера. Метод Хаусхолдера заключается в разложении матрицы A в виде мультипликации двух матриц (другими словами, происходит QR -факторизация):
к верхнетреугольной форме методом Хаусхолдера. Метод Хаусхолдера заключается в разложении матрицы A в виде мультипликации двух матриц (другими словами, происходит QR -факторизация):
A = T*H,
где T – квадратная ортогональная матрица, и H – верхнетреугольная прямоугольная матрица.
После чего условие минимизации можно переписать как:
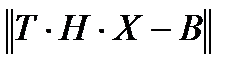 .
.
Так как T – ортогональная матрица, данное условие минимума равнозначно минимизации другой нормы:
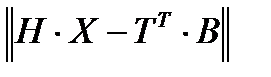 .
.
Верхнетреугольную матрицу H представим в виде:
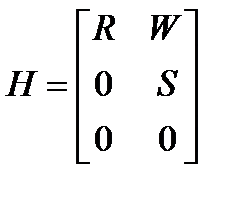 ,
,
где 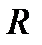 и
и 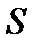 – верхнетреугольные матрицы, причем
– верхнетреугольные матрицы, причем 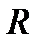 имеет размерность 3х3. При практической реализации верхнетреугольная форма вычисляется рекурсивно, по мере поступления данных в последовательные эпохи.
имеет размерность 3х3. При практической реализации верхнетреугольная форма вычисляется рекурсивно, по мере поступления данных в последовательные эпохи.
А матрицу, получающуюся из мультипликации 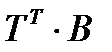 , обозначим как
, обозначим как 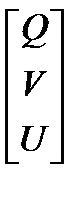 , так что
, так что
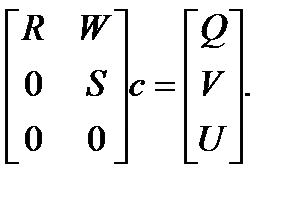
Можно заметить из уравнения, что матрица U не принимает участия в поиске с, поэтому нижняя часть получившейся системы линейных уравнений отбрасывается. Именно такая возможность, предоставляемая методом Хаусхолдера, и приводит к экономии времени и процессорной мощности обрабатывающего ЭВМ. Следовательно:
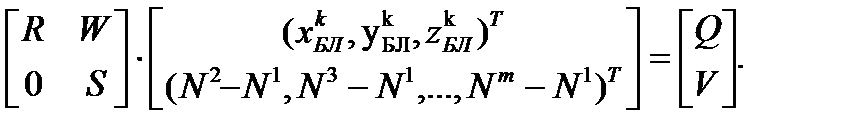
| ((2.22) |
Матричное уравнение (22) записывается как система двух уравнений:
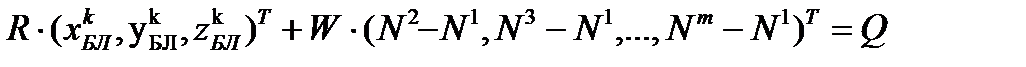
| ((2.23) |
и
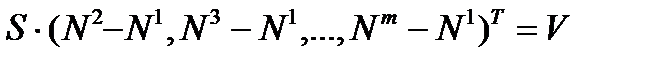
| ((2.24) |
Из (2.23) получаем вещественнозначное смешанное кодово-фазовое решение:
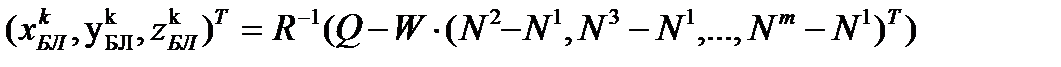 ,
,
где 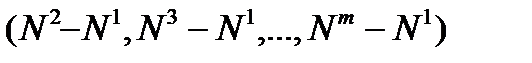 – вектор вещественных величин (вещественнозначных неопределенностей), полученный решением системы уравнений (24). Такое решение (без использования целочисленной природы неопределенностей) позволяет достичь точности в несколько дециметров.
– вектор вещественных величин (вещественнозначных неопределенностей), полученный решением системы уравнений (24). Такое решение (без использования целочисленной природы неопределенностей) позволяет достичь точности в несколько дециметров.
Для того чтобы получить высокую точность оценок положения для как можно минимального числа эпох, должна быть использована природа целочисленных неопределенностей. Заметим, что в нашем алгоритме мы только оценили 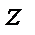 как вещественный вектор, но не определили его как целочисленный вектор. Для некоторых приложений этого будет достаточно, и для них не имеет смысла дополнительно тратить время вычислений для разрешения целочисленных неопределенностей. Также, если целочисленные неопределенности определены неправильно, это может вызвать большие ошибки в оценке положения.
как вещественный вектор, но не определили его как целочисленный вектор. Для некоторых приложений этого будет достаточно, и для них не имеет смысла дополнительно тратить время вычислений для разрешения целочисленных неопределенностей. Также, если целочисленные неопределенности определены неправильно, это может вызвать большие ошибки в оценке положения.
Имеется несколько подходов для разрешения целочисленных неопределенностей на базе вторых разностей. Один их хорошо известных подходов называется LAMBDA метод, смотри [14, глава 8]. На вход метода подаются вещественнозначные неопределенности (в качестве исходной оценки), матрица ковариации неопределенностей 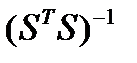 и требуемое количество векторов-кандидатов (на практике достаточно двух). Он основан на ковариации
и требуемое количество векторов-кандидатов (на практике достаточно двух). Он основан на ковариации 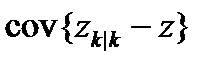 . Ковариация неопределенностей может быть найдена из (2.24):
. Ковариация неопределенностей может быть найдена из (2.24):
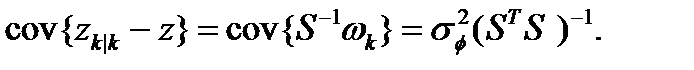
| ((2.25) |
Дадим теоретическое описание использования LAMBDA-метода при решении нашей задачи. Линейные системы уравнений, используемые в математической модели для решения задачи дифференциальной коррекции, можно представить в виде:
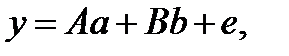
| ((2.26) |
где y – заданный вектор данных, a и b – неизвестные параметрические вектора и e – вектор шумов. Вектор данных y состоит из «наблюдаемых» минус «вычисленных» первых разностей по коду и фазе за весь временной промежуток наблюдений. a – вектор разностей целочисленных неопределенностей размерности {m-1}, измеряемые в циклах. Значения вектора a являются целыми. В векторе b размерности p заключены оставшиеся неизвестные параметры уравнений, такие как координаты базовой линий и тропосферные (ионосферные) параметры атмосферной задержки.
При использовании принципа наименьших квадратов, система (26) решается посредством минимизации:
 , , 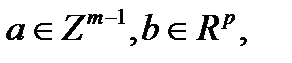
| ((2.27) |
где норма вычисляется по формуле 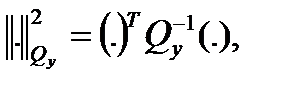
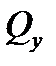 - матрица ковариации наблюдаемых величин,
- матрица ковариации наблюдаемых величин,
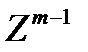 - целочисленное пространство размерности m-1.
- целочисленное пространство размерности m-1.
Для того чтобы решить такого рода задачу минимизации, необходимо сначала провести ортогональную декомпозицию целевой функции. Распишем целевую функцию в виде суммы трех квадратов,
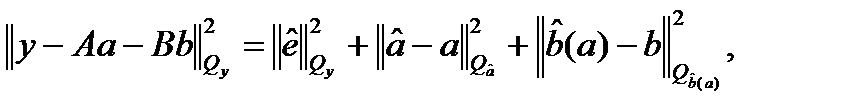
| ((2.28) |
где
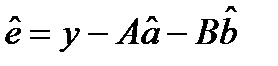 ,
,
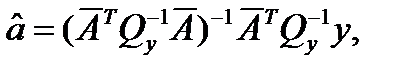
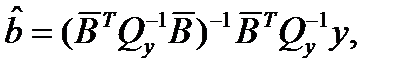
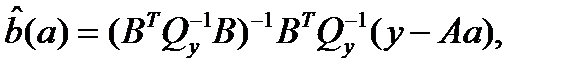
где 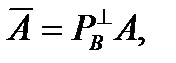
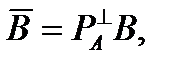 с ортогональными проективными операторами
с ортогональными проективными операторами 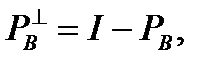
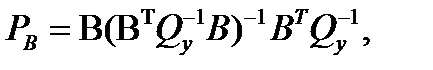
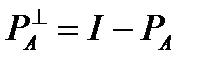 и
и 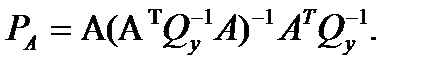 Матрица
Матрица 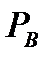 является ортогональным проективным оператором, который проецируется ортогонально вдоль направления B (относительно метрики
является ортогональным проективным оператором, который проецируется ортогонально вдоль направления B (относительно метрики 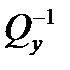 ). Аналогично, матрица
). Аналогично, матрица 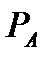 является ортогональным проективным оператором, который проецируется ортогонально вдоль направления A.
является ортогональным проективным оператором, который проецируется ортогонально вдоль направления A.
Ковариационные матрицы 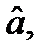
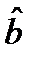 и
и 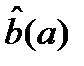 задаются формулами:
задаются формулами:
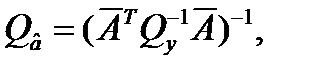
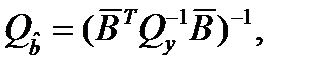
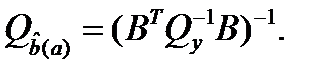
Вектора 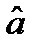 и
и 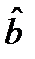 являются вектором веществозначных неопределенностей и вещественным решением. Они определяются из (2.24) и (2.23), то есть когда в задаче минимизации (2.27) отсутствует ограничение по целочисленности
являются вектором веществозначных неопределенностей и вещественным решением. Они определяются из (2.24) и (2.23), то есть когда в задаче минимизации (2.27) отсутствует ограничение по целочисленности 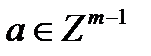 .
. 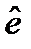 является остаточным вектором соответствующий веществозначному решению.
является остаточным вектором соответствующий веществозначному решению.