Оценка качества продукции, как правило, осуществляется на основе выборочного исследования. На практике из генеральной совокупности извлекается выборка заранее установленного объема. Элементы, принадлежащие данной выборке, выбираются случайным образом, например, с помощью таблицы случайных чисел. Распределения выборочных параметров называют выборочными. Для оценки математического ожидания распределения чаще всего используется арифметическое среднее. Это наилучшая оценка математического ожидания, если распределение является нормальным.
Основной целью анализа статистических данных являются выводы о свойствах и качестве всей генеральной совокупности. Статистические выводы относятся к генеральным совокупностям, а нек выборкам из них. Например, изучают результаты выборочных обследований только для того, чтобы оценить шансы кандидатов получить голоса от всех избирателей, участвующих в выборах. Аналогично менеджера по качеству выборочные показатели интересуют лишь потому, что они позволяют сделать выводы о качестве всей продукции компании. Выборочные параметры, в том числе, и выборочное среднее, полученное при обследовании конкретной выборки, само по себе интереса не представляют.
Арифметическое среднее[3] называется несмещенным (unbiased), поскольку среднее значение всех выборочных средних (при заданном объеме выборки п)равно математическому ожиданию генеральной совокупности.
Упражнение 4. Предположим, что генеральная совокупность – это оценки, которые получили три студента на экзамене по статистике. Каждый из них получил различные оценки: 3; 2 и 4.
Математическим ожиданием для данной генеральной совокупности будет сумма всех баллов совокупности, деленная на ее объем:
(9)
где μ — математическое ожидание генеральной совокупности;
N — объем генеральной совокупности;
Xi — i -й элемент генеральной совокупности;
— сумма всех элементов генеральной совокупности.
Средним квадратическим отклонением генеральной совокупности оценок будет корень квадратный из ее дисперсии:
(10)
Решение. Таким образом, для приведенных данных, имеем:
.
.
Если из этой генеральной совокупности необходимо извлечь выборку, состоящую из оценок двух студентов, то возникает 3 варианта выбора: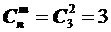 
.
Этим вариантам соответствуют следующие средние баллы:
| Вариант выборки (студенты) | Экзаменационные оценки | Средний балл выборки |
| 1и2 | 3и2 | 2,5 |
| 1и3 | 3и4 | 3,5 |
| 2и3 | 2и4 | |
Средний балл всех выборок, 
|
Если усреднить все варианты средних значений, мы получим величину μ 
, равную математичес к ому ожиданию генеральной совокупности μ, т.е. число равное 3.
Итак, среднее значениевсех выборочных средних равно математическому ожиданию генеральной совокупности. Следовательно, хотя нам неизвестно, насколько хорошо конкретное выборочноесреднее аппроксимирует математическое ожидание генеральной совокупности, среднее значение всех выборочных средних совпадает с математическим ожиданием генеральной совокупности.