Этот вид движения чаще всего относится к ползунам, движущимся относительно прямолинейных направляющих (рис. 5.1). Пусть при этом 
–это масса ползуна, 
– его ускорение.
Сила инерции элементарной массы звена 
. Если просуммировать все элементарные силы инерции данного ползуна, т. е. найти сумму 
, то получится главный вектор сил инерции звена, равный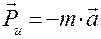 
. То есть главный вектор сил инерции, или просто сила инерции звена в его поступательном движении равна массе звена, помноженной на его ускорение. Знак «минус» в правой части формулы указывает на противоположность направления силы инерции по отношению к ускорению.
Вращательное движение звена
В этом движении находятся кривошипы, кулисы, коромысла и другие звенья механизмов. Возьмём стержневое звено ОА (рис. 5.2), вращающееся вокруг неподвижной точки О.
Масса звена равна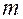 
, момент инерции относительно центра масс S равен 
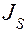. Вращение происходит с угловой скоростью 
и угловым ускорением 
. Расстояние между центром масс и центром вращения равно 
.
Вычислим ускорение, с которым движется центр масс S. Его нормальное ускорение равно 
, тангенциальное ускорение равно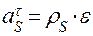 
. Так как эти составляющие полного ускорения перпендикулярны друг другу, то полное ускорение равно 
. 
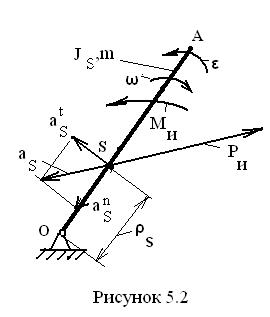В результате наличия этого ускорения возникает сила инерции, приложенная в центре масс, направленная противоположно ускорению центра масс
.
Угловое ускорение звена вызывает появление инерционного момента (или момента сил инерции), направленного по отношению к нему в противоположную сторону
.
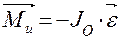В этой формуле момент инерции принимается относительно центра вращения и определяется формулой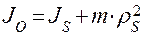 
.
Частные случаи
1. 
. 2. 
.
3. 
.
Плоско-параллельное движение звена
Такое движение совершают чаще всего шатуны механизмов. На рис. 5.3 изображён шатун, совершающий такое движение. Масса шатуна равна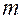 
, момент 
инерции относительно центра масс равен .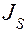
Звено движется, имея угловое ускорение 
и ускорение центра масс 
. Аналогично вращательному движению в этом случае также будут действовать оба инерционных фактора: сила инерции 
, противоположная ускорению, и момент сил инерции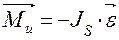 
, противоположный угловому ускорению
20. Общие положения силового расчета механизмов (принцип Даламбера, принцип освобождаемости, статическая определимость групп Ассура, порядок силового расчёта механизма).
Принцип Даламбера
Силовой расчёт механизмов выполняется на основе принципа Даламбера, позволяющего рассматривать подвижные системы, к которым относятся механизмы, как неподвижные, находящиеся в равновесии. Принцип Даламбера можно сформулировать так: если к системе сил, действующих на подвижную систему, добавить силы инерции, то такую систему можно рассматривать как находящуюся в равновесии, и к ней применимы законы статики.
Принцип освобождаемости
Если рассматривать механизм в целом, то имеющаяся в каждой кинематической паре, согласно принципу равенства действия и противодействия, пара сил (реакций), действующих по одной линии действия и равных по величине, уравновешивается и на равновесие механизма в целом не влияет. Так что даже в простом механизме определить эти реакции невозможно – они не войдут в уравнения равновесия. Для определения реакций необходимо механизм расчленить на части, каждая из которых была бы статически определима и в которой неизвестные реакции входили бы в число внешних сил и в уравнения равновесия.