Приведённым моментом инерции механизма называется момент инерции условного диска, которым заменяется реальный механизм, обладающего кинетической энергией, равной сумме кинетических энергий всех звеньев механизма.
Кинетическая энергия условного диска  , где
, где 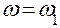 , т. е. угловая скорость звена приведения, равная угловой скорости кривошипа.
, т. е. угловая скорость звена приведения, равная угловой скорости кривошипа.
Кинетическая энергия звена, совершающего поступательное движение,  , где
, где  – масса звена,
– масса звена,  – скорость звена.
– скорость звена.
Кинетическая энергия звена, совершающего вращательное движение,  , где
, где  – момент инерции звена,
– момент инерции звена,  – угловая скорость звена.
– угловая скорость звена.
Кинетическая энергия звена в плоскопараллельном движении  , где
, где  – масса звена,
– масса звена,  – скорость центра масс звена,
– скорость центра масс звена,  – момент инерции звена относительно его центра масс,
– момент инерции звена относительно его центра масс,  – угловая скорость звена. Согласно определению имеем:
– угловая скорость звена. Согласно определению имеем:
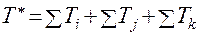 .
.
Подставив сюда записанные выше выражения кинетических энергий и, решая затем полученное равенство относительно  , запишем
, запишем
 .
.
Как видно из этой формулы, приведённый момент инерции зависит от структуры механизма, от массовых характеристик звеньев, от положения механизма и не зависит от угловой скорости ведущего звена. Некоторые механизмы имеют постоянное значение приведённого момента инерции. Машины, в основе которых механизмы с  , называются ротативными.
, называются ротативными.
28. Динамическая модель машины; приведённый момент сил сопротивления технологической машины.
Приведённым моментом сил сопротивления называется момент, приложенный к звену приведения, мгновенная мощность которого равна сумме мгновенных мощностей всех сил сопротивления, действующих в механизме.
Мгновенная мощность приведённого момента сопротивления  . Мгновенная мощность
. Мгновенная мощность  -той силы сопротивления
-той силы сопротивления  . Согласно определению
. Согласно определению  , поэтому, подставив сюда соответствующие выражения, получаем
, поэтому, подставив сюда соответствующие выражения, получаем  , откуда
, откуда
 .
.
Если среди сил сопротивления имеются моменты, то их можно представить в виде пар сил с плечами, равными длинам соответствующих звеньев.
З а м е ч а н и е. Если во всех математических выражениях заменить силы сопротивления движущими силами, то в результате получится приведённый момент движущих сил:
 .
.
Зависимость приведённых моментов сил от угла поворота, скорости или времени называется механической характеристикой машины.
29. Характеристика режима пуска машины.
30. Характеристики установившегося неравновесного и равновесного движения машины.
31. Характеристика режима остановки
Анализ динамики машин производится на основе теоремы об изменении кинетической энергии системы: изменение (приращение) кинетической энергии системы на её возможном перемещении равно сумме работ всех внешних и внутренних сил на этом перемещении, то есть
 ,
,
где 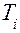 –кинетическая энергия системы в данный момент времени;
–кинетическая энергия системы в данный момент времени;  – кинетическая энергия системы в последующий момент времени;
– кинетическая энергия системы в последующий момент времени;  – работа движущих сил при перемещении системы из
– работа движущих сил при перемещении системы из  -го до
-го до 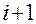 -го положения системы;
-го положения системы; 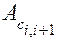 – работа сил сопротивления на том же перемещении системы. Сумма работ в правой части равенства называется избыточной работой
– работа сил сопротивления на том же перемещении системы. Сумма работ в правой части равенства называется избыточной работой  .
.
В зависимости от соотношения величин правой части этого равенства различают следующие режимы (виды) движения машин.
I. Неустановившийся режим
А) Пуск (разбег). Этот режим имеет место при соотношении работ  или
или  . Тогда в левой части имеет место соотношение
. Тогда в левой части имеет место соотношение  , т. е. кинетическая энергия машины возрастает, и возрастает угловая скорость
, т. е. кинетическая энергия машины возрастает, и возрастает угловая скорость  . Графически это можно представить как на рис. 6.2.
. Графически это можно представить как на рис. 6.2.
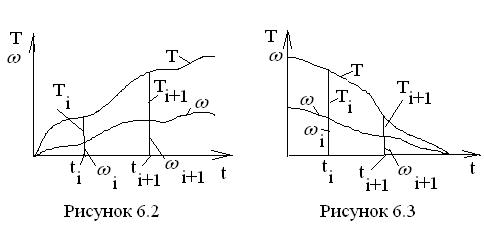
Б). Остановка (выбег) имеет место при обратном соотношении работ, т. е.  и
и  . При этом кинетическая энергия машины убывает, и угловая скорость также убывает. Графически этот режим представлен на рис. 6.3. Оба режима не являются рабочими, так как не могут продолжаться долго. Режим пуска заканчивается, когда угловая скорость начинает повторять свои значения, а режим остановки заканчивается полной остановкой машины. При исследовании этих режимов, кроме закона изменения угловой скорости, определяется время пуска или, соответственно, остановки.
. При этом кинетическая энергия машины убывает, и угловая скорость также убывает. Графически этот режим представлен на рис. 6.3. Оба режима не являются рабочими, так как не могут продолжаться долго. Режим пуска заканчивается, когда угловая скорость начинает повторять свои значения, а режим остановки заканчивается полной остановкой машины. При исследовании этих режимов, кроме закона изменения угловой скорости, определяется время пуска или, соответственно, остановки.
II. Установившийся режим
А) Неравновесный. Режим характеризуется тем, что работа движущих сил то больше, то меньше работы сил сопротивления, т. е. в течение цикла имеют место следующие соотношения  и
и  . Но за цикл работы машины эти величины одинаковы
. Но за цикл работы машины эти величины одинаковы  , так что в начале и в конце цикла
, так что в начале и в конце цикла  .
.
В результате таких соотношений работ кинетическая энергия машины и угловая скорость ведущего звена в течение цикла изменяются периодически, причём средние значения как кинетической энергии, так и угловой скорости остаются постоянными. Графически характер изменения кинетической энергии и угловой  скорости представлен на рис. 6.4. Средняя угловая скорость определяется соотношением
скорости представлен на рис. 6.4. Средняя угловая скорость определяется соотношением 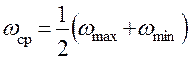 . Величина, характеризующая отклонение максимальной и минимальной угловой скорости от её среднего значения, называется коэффициентом неравномерности
. Величина, характеризующая отклонение максимальной и минимальной угловой скорости от её среднего значения, называется коэффициентом неравномерности  . Численно коэффициент
. Численно коэффициент  равен
равен  .
.
Для поддержания изменения угловой скорости в заданных пределах в машинах применяют маховики, представляющие собой колёса с массивным ободом, устанавливаемые на вал ведущего звена и вращающиеся с его угловой скоростью.
Данный режим является рабочим, так как может продолжаться неопределённо долго. В этом режиме работают все машины циклического действия.
Б) Равновесный. Этот режим имеет место в тех машинах, в которых работа движущих сил постоянно равна работе сил сопротивления, т. е.  . Избыточная работа в течение всего цикла равна нулю,
. Избыточная работа в течение всего цикла равна нулю, 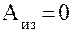 . Кинетическая энергия и угловая скорость остаются постоянными (рис. 6.5).
. Кинетическая энергия и угловая скорость остаются постоянными (рис. 6.5).
Такой режим работы характерен для ротативных машин.
32. Решение прямой задачи динамики аналитическим методом
33. В пизду, не нашел, хуйня какая то=(
34. Определение момента инерции маховика с помощью диаграммы энергомасс. И 35 Роль маховика в машине.
Маховик служит для уменьшения колебаний величины угловой скорости ведущего звена, уменьшения угловых ускорений и, в конечном итоге, инерционных воздействий. Этот эффект, называемый кинематическим, тем больше, чем больше момент инерции маховика. Кинематический эффект тесно связан с динамическим, который заключается в том, что маховик выступает как аккумулятор кинетической энергии. Он накапливает кинетическую энергию в те промежутки времени, когда возрастает его угловая скорость, принимая на себя часть избыточной работы, которая в этом случае не тратится на разгон машины. При уменьшении угловой скорости маховик отдаёт часть накопленной энергии, помогая движущим силам выполнять полезную работу и препятствуя существенному уменьшению угловой скорости. Некоторые машины, например машины ударного действия, без такой помощи не смогли бы функционировать.
 Для расчёта момента инерции маховика примем допущение, что максимальный перепад кинетической энергии машины, численно равный максимальному перепаду избыточной работы, поглощается маховиком. Для иллюстрации этого служит рис. 6.6. Допущение здесь заключается в том, что часть кинетической энергии поглощается звеньями механизма, чем мы пренебрегаем. Обозначим перепад избыточной работы
Для расчёта момента инерции маховика примем допущение, что максимальный перепад кинетической энергии машины, численно равный максимальному перепаду избыточной работы, поглощается маховиком. Для иллюстрации этого служит рис. 6.6. Допущение здесь заключается в том, что часть кинетической энергии поглощается звеньями механизма, чем мы пренебрегаем. Обозначим перепад избыточной работы  . Согласно принятому допущению эта величина составляет разность между максимальным и минимальным значениями кинетической энергии маховика:
. Согласно принятому допущению эта величина составляет разность между максимальным и минимальным значениями кинетической энергии маховика:  ,
,
то есть  .
.
Максимальная величина кинетической энергии маховика вычисляется по формуле
 ,
,
минимальная величина вычисляется по формуле
 .
.
Поэтому разность этих величин даёт выражение
 .
.
Разложив разность квадратов в скобках на множители и заменив последние их выражениями, полученными из приведенных выше формул для вычисления 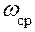 и
и  , получаем
, получаем
 .
.
Объединяя результаты выкладок, запишем  и
и  , откуда окончательно получаем
, откуда окончательно получаем
 .
.
Как видно из этой формулы, достичь полного постоянства угловой скорости невозможно, так как для этого необходимо иметь бесконечно большой маховик (требуется 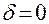 ). Ясно также, что увеличение скорости вращения маховика ведёт к уменьшению его массы и размеров, поэтому целесообразно маховик устанавливать на более быстроходный вал.
). Ясно также, что увеличение скорости вращения маховика ведёт к уменьшению его массы и размеров, поэтому целесообразно маховик устанавливать на более быстроходный вал.
36. Понятие о передаточном отношении в зубчатом механизме
Основной характеристикой преобразования вращательного движения зубчатых механизмов является передаточное отношение – отношение угловой скорости или частоты вращения ведущего звена механизма к угловой скорости или частоте вращения ведомого звена.
Передаточное отношение обозначается латинской буквой « » с индексами. Индексы указывают на то, от какого колеса (1-й индекс) к какому (2-й индекс) вычисляется передаточное отношение. Например,
» с индексами. Индексы указывают на то, от какого колеса (1-й индекс) к какому (2-й индекс) вычисляется передаточное отношение. Например,  12 обозначает передаточное отношение от первого колеса ко второму. Согласно определению
12 обозначает передаточное отношение от первого колеса ко второму. Согласно определению
 или
или  , так как
, так как 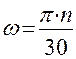 .
.
Поскольку  21=
21=  2/
2/  1, то
1, то 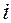 12·
12· 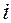 21 =1, и
21 =1, и  21 =1/
21 =1/  12.
12.
Если в механизме передаточное отношение больше единицы, то угловая скорость ведущего колеса больше, чем ведомого, и такой механизм называется редуктором. В противном случае механизм называется мультипликатором. Редукторы в машиностроении применяются в большинстве случаев из-за необходимости уменьшения скоростей движения исполнительных органов машин и увеличения на них усилий. Мультипликаторы применяются реже и не являются силовыми устройствами.
При совпадении направлений вращения ведущего и ведомого колёс передаточное отношение имеет положительный знак, т. е.  , если направления вращений не совпадают, то
, если направления вращений не совпадают, то  . Заметим, что знак имеет смысл при параллельных осях колёс.
. Заметим, что знак имеет смысл при параллельных осях колёс.
37. Передаточное отношение простой зубчатой передачи.
 Простая зубчатая передача – трехзвенный зубчатый механизм, состоящий из двух зубчатых колес и стойки. В зубчатых колесах существуют окружности, которые при передаче движения перекатываются друг по другу без скольжения. Эти окружности называются центроидными, т. к. каждая из них является геометрическим местом центров мгновенного относительного вращения другой окружности. На рис. 2.1 показана такая передача. В ней колесо 1 вращается вокруг центра O1, а колесо 2 – вокруг центра O2. Их центроидные окружности касаются друг друга в точке A. Направления вращения колёс указаны стрелками. В точке A окружные скорости колёс одинаковы и определяются произведением угловых скоростей колёс на радиусы центроидных окружностей
Простая зубчатая передача – трехзвенный зубчатый механизм, состоящий из двух зубчатых колес и стойки. В зубчатых колесах существуют окружности, которые при передаче движения перекатываются друг по другу без скольжения. Эти окружности называются центроидными, т. к. каждая из них является геометрическим местом центров мгновенного относительного вращения другой окружности. На рис. 2.1 показана такая передача. В ней колесо 1 вращается вокруг центра O1, а колесо 2 – вокруг центра O2. Их центроидные окружности касаются друг друга в точке A. Направления вращения колёс указаны стрелками. В точке A окружные скорости колёс одинаковы и определяются произведением угловых скоростей колёс на радиусы центроидных окружностей  1 и
1 и  2, т. е. соответственно VA1=
2, т. е. соответственно VA1=  1·
1·  1 и VA2=
1 и VA2=  2·
2·  2. А так как эти скорости равны, то имеет место равенство:
2. А так как эти скорости равны, то имеет место равенство:
 ,
,
из которого следует, что передаточное отношение может быть выражено через отношение радиусов центроидных окружностей, то есть
 .
.
Знаки «+» и «–» перед отношением радиусов появились в связи с тем, что в отличие от угловых скоростей радиусы не могут быть отрицательными, и знак «–» относится к данной схеме, а знак «+» имел бы место при внутреннем зацеплении колёс.
Если центроидными окружностями являются делительные окружности, то их радиусы можно выразить следующим образом. Длины центроидных окружностей S1 первого колеса и S2 второго колеса определяются выражениями соответственно:
S1 = 2· π·  1 = p·
1 = p·  1 и S2 =2· π·
1 и S2 =2· π·  2 = p·
2 = p·  2,
2,
где p – шаг колёс по делительной окружности, т. е. расстояние между одноимёнными точками двух соседних зубьев,  1 и
1 и  2 – числа зубьев данных колёс, (то же, что число шагов).
2 – числа зубьев данных колёс, (то же, что число шагов).
Решим эти выражения относительно радиусов  1 и
1 и  2:
2:
 1 = p·z1/(2·π),
1 = p·z1/(2·π),  2 = p·z2/(2·π).
2 = p·z2/(2·π).
Отношение шага по делительной окружности к числу π называется модулем зубчатого колеса, который обозначается латинской буквой m. Модуль, как и шаг, является единым для колёс, находящихся в зацеплении. Он измеряется в миллиметрах, и через него выражаются все размеры зубьев (величины модулей определяются стандартом). Подставив теперь вместо радиусов в ранее записанном выражении передаточного отношения их найденные выше значения, после сокращения на 2 и на m, получим окончательно
 .
.
То есть, передаточное отношение простой зубчатой передачи может быть выражено как обратное отношение чисел зубьев колёс. Это правило справедливо при всех способах расположения осей колёс в пространстве.
38..Передаточное отношение зубчатого механизма с рядовым соединением колёс
В этом механизме все колеса вращаются в одной плоскости, и каждое промежуточное колесо образует зацепление с двумя соседними (рис. 2.2).
 На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
Согласно доказанному выше положению общее передаточное отношение данного механизма определяется равенством:
 14 =
14 =  12 ·
12 ·  23·
23·  34.
34.
Записав передаточные отношения отдельных ступеней
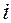 12 = –
12 = –  2/
2/  1,
1,  23 = –
23 = –  3/
3/  2 и
2 и  34 = –
34 = –  4/
4/  3
3
и подставив их в правую часть полученного ранее произведения, имеем
 14 = (–
14 = (–  2/
2/  1)·(–
1)·(–  3/
3/  2)·(–
2)·(–  4/
4/  3),
3),
что после выполнения необходимых действий приводит к следующему результату
 14 = –
14 = –  4/
4/  1.
1.
Этот результат показывает, что в механизмах такого типа передаточное отношение зависит только от чисел зубьев ведущего и ведомого колёс. Промежуточные колёса, числа зубьев которых не влияют на передаточное отношение, называются паразитными. Они позволяют только передать движение на небольшое расстояние и изменить его знак. Для общего случая механизма с произвольным числом колёс при вычислении передаточного отношения можно руководствоваться следующим выражением  ,
,
где k – число внешних зацеплений, т. к. только они влияют на знак результата.
39. Передаточное отношение зубчатого механизма со ступенчатым соединением колёс.
 В этом механизме колеса вращаются в параллельных плоскостях, и каждое промежуточное колесо вступает в зацепление с одним соседним колесом. На каждом промежуточном валу имеется по два колеса. На рисунке 2.3 показана схема
В этом механизме колеса вращаются в параллельных плоскостях, и каждое промежуточное колесо вступает в зацепление с одним соседним колесом. На каждом промежуточном валу имеется по два колеса. На рисунке 2.3 показана схема
механизма, в котором на промежуточных валах вращаются колёса 2 и 3, 4 и 5, 6 и 7, на ведущем валу находится одно колесо 1, а на ведомом – также одно колесо 8. Найдём передаточное отношение от первого колеса к восьмому 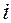 18. Для этого сначала запишем
18. Для этого сначала запишем
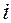 18 =
18 =  12 ·
12 · 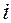 34 ·
34 ·  56 ·
56 ·  78.
78.
Так как 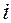 12 = –
12 = –  2/
2/  1,
1, 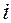 34 = –
34 = –  4/
4/  3,
3, 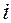 56 =
56 =  6/
6/  5 и
5 и 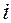 78 = –
78 = –  8/
8/  7, то, подставив в произведение передаточных отношений эти дроби, получим окончательно
7, то, подставив в произведение передаточных отношений эти дроби, получим окончательно
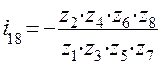 .
.
Никаких сокращений здесь нет кроме возможных общих множителей после подстановки чисел зубьев. Общий знак минус появился из-за того, что в механизме нечётное число пар внешнего зацепления (три пары). По сравнению с предыдущей схемой здесь можно получить практически любое передаточное отношение. Для общего случая механизма запишем формулу передаточного отношения в следующем виде
 ,
,
где k – число пар колёс внешнего зацепления, а символы в числителе означают произведение чисел зубьев ведомых колёс каждой пары, в знаменателе – произведение чисел зубьев ведущих колёс каждой пары.
Такие механизмы более выгодны с точки зрения преобразования движения, чем механизмы с рядовым соединением колес, т.к. они позволяют получить любое передаточное отношение.
40. Типовая схема зубчатого механизма планетарного типа.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:
- однорядный планетарный механизм;
- двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением
- двухрядный планетарный механизм с двумя внешними зацеплениями;
- двухрядный планетарный механизм с двумя внутренними зацеплениями.
Элементы планетарного механизма имеют специальные названия:
- зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
- колесо с внутренними зубьями называют "короной" или "эпициклом";
- колеса, оси которых подвижны, называют "сателлитами";
- подвижное звено, на котором установлены сателлиты, называют "водилом". Звено водила принято обозначать не цифрой, а латинской буквой h.
В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.
Таблица 15.1
Типовые планетарные механизмы
| № | Структурная схема механизма | Uред | КПД |

| 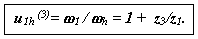 3....10
3....10
| 0.97....0.99 | |

|  7....16
7....16
| 0.96....0.98 |
41. Аналитическое исследование кинематики зубчатого механизма планетарного типа.
Для аналитического решения задач кинематики, при котором в дифференциальном механизме по заданным угловым скоростям ведущих звеньев определяется угловая скорость ведомого звена, а в планетарном механизме определяется передаточное отношение от ведущего звена к ведомому, применяют метод обращения движения. Он заключается в том, что всему механизму вместе со стойкой сообщается движение с угловой скоростью, равной и противоположно направленной угловой скорости водила. Тогда при сохранении характера относительного движения звеньев водило останавливается, а все звенья получают угловые скорости, уменьшенные на угловую скорость водила. Механизм в таком случае превращается в условный механизм с неподвижными осями колес. Это позволяет составить следующую таблицу скоростей:
| № звена | Угловые скорости звеньев в реальном механизме | Угловые скорости звеньев в механизме с условно неподвижным водилом |
| H |  1 1
 2 2
 3 3
 H H
|  1(H)= 1(H)=  1 – 1 –  H H
 2(H= 2(H=  2 – 2 –  H H
 3(H)= 3(H)=  3 – 3 –  H H
 H(H)= H(H)=  H – H –  H =0 H =0
|
Записываем передаточное отношение от первого центрального колеса к третьему 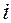 13(H) при условно неподвижном водиле. Для схемы, представленной на рисунке 2.4, запишем
13(H) при условно неподвижном водиле. Для схемы, представленной на рисунке 2.4, запишем  13(H) =
13(H) =  1(H)⁄
1(H)⁄  3(H), или после подстановки соответствующих разностей из таблицы получаем
3(H), или после подстановки соответствующих разностей из таблицы получаем
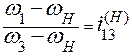 . (а)
. (а)
Из трех величин левой части две должны быть заданы, третья определяется решением данного уравнения.
В планетарном механизме, как сказано выше, одно из центральных колес неподвижно. Если принять колесо 3 с внутренними зубьями за неподвижное, т.е. принять  3 = 0, то уравнение (а) запишется в виде
3 = 0, то уравнение (а) запишется в виде  13(H) = (
13(H) = (  1 ⁄
1 ⁄  H)/–
H)/–  H. Разделив почленно числитель на знаменатель и заменив отношения угловых скоростей обозначениями передаточных отношений, получим окончательно:
H. Разделив почленно числитель на знаменатель и заменив отношения угловых скоростей обозначениями передаточных отношений, получим окончательно:
 , (б)
, (б)
т. е. передаточное отношение в планетарном механизме от любого центрального колеса к водилу равно единице минус передаточное отношение от этого центрального колеса к другому центральному колесу в механизме с условно неподвижным водилом.
42. Графический расчёт кинематики зубчатых механизмов (теоретические основы, применение).
 Методика графического расчёта основана на том, что окружные скорости центроидных окружностей колес одинаковы, а в точке касания этих окружностей их направления совпадают. Зубчатые колёса, показанные на рисунке 2.6, вращаются навстречу друг другу так, что в точке А касания их центроидных окружностей окружные скорости совпадающих точек А1 и А2 также совпадают. Имея в виду, что скорость точки, совершающей вращательное движение вокруг неподвижной точки, линейно зависит от её расстояния от последней, то есть
Методика графического расчёта основана на том, что окружные скорости центроидных окружностей колес одинаковы, а в точке касания этих окружностей их направления совпадают. Зубчатые колёса, показанные на рисунке 2.6, вращаются навстречу друг другу так, что в точке А касания их центроидных окружностей окружные скорости совпадающих точек А1 и А2 также совпадают. Имея в виду, что скорость точки, совершающей вращательное движение вокруг неподвижной точки, линейно зависит от её расстояния от последней, то есть
V =  · r,
· r,
заключаем, что концы векторов скоростей точек, лежащих на прямой О1О2, принадлежащих колесу 1, лежат на одной прямой, называемой линией распределения скоростей этого колеса. То же самое имеет место и с точками колеса 2, лежащими на линии центров колёс.
Проведём горизонтальную прямую ниже изображения колёс и на некотором расстоянии от этой прямой возьмём произвольную точку P. Из неё проведём прямые параллельно линиям распределения скоростей до пересечения с горизонталью в точках 1 и 2. Запишем цепочку равенств, имея в виду предыдущие рассуждения и подобие треугольников на картине зацепления и на нижнем построении:
 12 =
12 =  .
.
Учитывая начало этого равенства и его конец, можно сделать вывод, что отрезки, полученные на горизонтали, в некотором масштабе изображают угловые скорости колёс. Для определения масштаба угловых скоростей необходимо угловую скорость  1 (если, конечно, она задана) поделить на отрезок
1 (если, конечно, она задана) поделить на отрезок  , измеренный в миллиметрах. Угловая скорость
, измеренный в миллиметрах. Угловая скорость  2 определится умножением этого масштаба на отрезок
2 определится умножением этого масштаба на отрезок  , взятый также в миллиметрах. На основе изложенной методики можно достаточно просто решить задачу кинематики любого зубчатого механизма. Если требуется определить передаточное отношение механизма, то достаточно взять отношение отрезков, выражающих соответствующие угловые скорости.
, взятый также в миллиметрах. На основе изложенной методики можно достаточно просто решить задачу кинематики любого зубчатого механизма. Если требуется определить передаточное отношение механизма, то достаточно взять отношение отрезков, выражающих соответствующие угловые скорости.
З а м е ч а н и е. В дифференциальных механизмах с замкнутым контуром (схема В рис. 2.5), как правило, ведущим звеном является центральное колесо дифференциальной ступени, и построение картины линейных скоростей от этого колеса невозможно. Для решения задачи необходимо выбрать в качестве ведущего любое другое звено и задаться произвольно его окружной скоростью. После этого задача решается без затруднений.