Профиль «Техника и технологии»
Задание 1.
Из леса по прямолинейному шоссе, перпендикулярному опушке леса, с постоянной скоростью 
выезжает автобус. По лугу вдоль опушки с постоянной скоростью 
едет мотоциклист (рис.).
Мотоциклист увидел автобус и тотчас устремился за ним в погоню. Скорость мотоцикла 
постоянна по величине и все время направлена в ту точку, где находится в данный момент автобус. Исходное расстояние между мотоциклистом и автобусом равно 
.
1. Если в момент времени 
вектор скорости мотоциклиста составляет угол 
с его первоначальным направлением, а расстояния 
, 
и 
равны 
, 
и 
соответственно, то малые изменения расстояний по модулю 
, 
и 
за малый интервал времени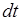 
определяются соотношениями …;
2. Расстояние 
, на котором мотоциклист догонит автобус, выражается через скорости мотоциклиста и автобуса следующим образом …
3. Время 
, через которое это произойдет, равно …
Варианты ответов:
1. 
2. 
3. 
1. 
2. 
3.
1. 
2. 3. 
1. 
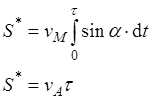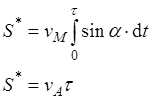2. 3. 
Задание 2.
Идеальный газ массой 
и молярной массой 
имеет температуру 
. Газ быстро, но не адиабатически, сжали, уменьшив объем в два раза. При этом установившаяся температура газа стала равной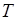 
.
1. Если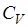 
— молярная теплоемкость идеального газа при постоянном объеме, то бесконечно малое изменение энтропии 
при сжатии газа на малый объем 
, определяется выражением вида ….
2. Если 
— коэффициенту Пуассона, где 
— молярная теплоемкость идеального газа при постоянном давлении, то изменение энтропии 
в ходе рассматриваемого процесса определяется выражением…
Варианты ответов:
1. 
2. 
1. 
2. 
1. 
2. 
1. 
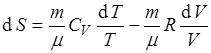2. 
Задание 3.
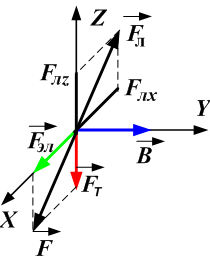
Частица массой и зарядом 
движется с постоянной по модулю скоростью в области пространства, где имеются три взаимно перпендикулярных поля: электрическое с напряженностью 
, магнитное с индукцией 
и поле тяжести 
(рис.).
В некоторый момент времени поля и выключают. Если минимальная кинетическая энергия частицы в процессе движения составляет половину начальной, то проекции скорости частицы на направления всех трех полей в момент выключения определяются выражениями …
Варианты ответов:
1. 
; 
; 
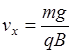2. 
; 
; 
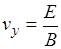3. 
; 
; 
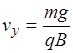4. ; ; 
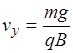Задания №4, №5, №6, №7 являются составными частями одного общего IV задания.
Задание 4.
Длинный тонкий гибкий ковер лежит на полу. Один край ковра загнули и с горизонтальной скоростью, изменяющейся по закону 
, где 
– постоянная, 
– расстояние от начальной точки, потянули над той частью ковра, которая покоится (рис.).
Если ковер имеет длину и массу 
, то выражение для импульса загнутой части ковра в зависимости от координаты перемещающегося края имеет вид …
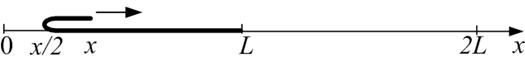
Варианты ответов:
1. 
2. 
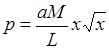
3. 
4. 
Задание 5.
Длинный тонкий гибкий ковер лежит на полу. Один край ковра загнули и с горизонтальной скоростью, изменяющейся по закону , где – постоянная, – расстояние от начальной точки, потянули над той частью ковра, которая покоится (рис.).
Ковер имеет длину и массу . Выберите все верные выражения для силы, действующей на загнутую часть ковра, в зависимости от координаты перемещающегося края.
Варианты ответов:
1. 
, где — масса движущейся части ковра в некоторый момент времени
2. 
3. 
4. 
, где — масса движущейся части ковра в некоторый момент времени
Задание 6.
Длинный тонкий гибкий ковер лежит на полу. Один край ковра загнули и с горизонтальной скоростью, изменяющейся по закону , где – постоянная, – расстояние от начальной точки, потянули над той частью ковра, которая покоится (рис.).
Если ковер имеет длину 
и массу , то работа 
силы 
, действующей на перемещающуюся часть ковра, совершенная к моменту начала движения всего ковра, и кинетическая энергия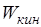 
ковра в этот момент времени равны …
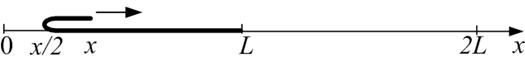
Варианты ответов:
1. 
; 
2. 
; 
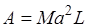3. 
; 
4. ; 
Задание 7.
Длинный тонкий гибкий ковер лежит на полу. Один край ковра загнули и с горизонтальной скоростью, изменяющейся по закону , где – постоянная, 
– расстояние от начальной точки, потянули над той частью ковра, которая покоится (рис.).
Если ковер имеет длину и массу 
, то к моменту начала движения всего ковра отношение 
, где 
– рассеиваемое тепло, – работа силы , действующей на перемещающуюся часть ковра, равно …
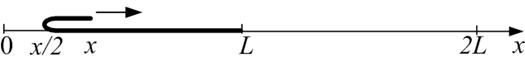
Варианты ответов
1. 
2. 
3. 
4. 0
Задания №8, №9, №10, №11 являются составными частями одного общего V задания.
Задание 8.
Пожарный шланг массой и длиной смотан в рулон радиусом 
, причем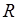 
<< (рис.).
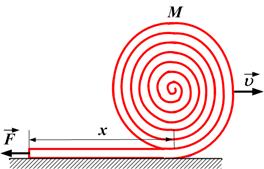
Рулону придали начальную скорость 
(угловая скорость 
), в то время как свободный конец шланга удерживают неподвижно. Если при разворачивании шланга изменением потенциальной энергии рулона и небольшой вертикальной составляющей скорости, приобретаемой при уменьшении радиуса рулона, можно пренебречь, то закон сохранения механической энергии для рулона после прохождения им расстояния записывается следующим образом: …
(Считать шланг идеально гибким; сопротивлением воздуха и трением качения пренебречь.)
Варианты ответов:
1. 
, где 
— момент инерции рулона радиусом 
, в который был скатан шланг массой , 
— момент инерции движущейся части рулона радиусом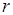 
массой 
2. 
, где — момент инерции движущейся части рулона радиусом 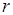массой
3. 
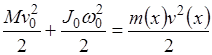, где — момент инерции рулона радиусом 
, в который был скатан шланг массой , — масса движущейся части рулона
4. 
, где — масса движущейся части рулона
Задание 9.
Пожарный шланг массой и длиной смотан в рулон радиусом 
, причем 
<< (рис.).
Рулону придали начальную скорость (угловая скорость ), в то время как свободный конец шланга удерживают неподвижно. Если при разворачивании шланга изменением потенциальной энергии рулона и небольшой вертикальной составляющей скорости, приобретаемой при уменьшении радиуса рулона, можно пренебречь, то зависимость скорости 
перемещающейся части рулона от пройденного им расстояния 
имеет вид …
(Считать шланг идеально гибким; сопротивлением воздуха и трением качения пренебречь.)
Варианты ответов:
1. 
2. 
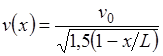
3. 
4. 
Задание 10.
Пожарный шланг массой 
и длиной 
смотан в рулон радиусом 
, причем 
<< (рис.).
Рулону придали начальную скорость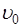 
(угловая скорость ), в то время как свободный конец шланга удерживают неподвижно. Если при разворачивании шланга изменением потенциальной энергии рулона и небольшой вертикальной составляющей скорости, приобретаемой при уменьшении радиуса рулона, можно пренебречь, то импульс системы определяется выражением …
(Считать шланг идеально гибким; сопротивлением воздуха и трением качения пренебречь.)
Варианты ответов:
1. 
2. 
3. 
4. 
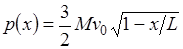
Задание11.
Пожарный шланг массой 
и длиной смотан в рулон радиусом , причем << (рис.).
Рулону придали начальную скорость 
(угловая скорость 
), в то время как свободный конец шланга удерживают неподвижно. Если при разворачивании шланга изменением потенциальной энергии рулона и небольшой вертикальной составляющей скорости, приобретаемой при уменьшении радиуса рулона, можно пренебречь, то результирующая сила 
, удерживающая неподвижный конец шланга, равна …
(Считать шланг идеально гибким; сопротивлением воздуха и трением качения пренебречь.)
Варианты ответов:
1. 
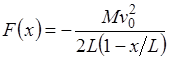
2. 
3. 
4. 