Для того, чтобы вывести основные соотношения, с помощью кото-рых можно произвести габаритный расчет оптической системы в слу-чае формирования гауссова пучка, рассмотрим преобразование пучка тонкой безаберрационной линзой. Пусть на линзу, которая задается своим фокусным расстоянием f ʹ (для определенности будем рассма-тривать положительную линзу), падает слева гауссов пучок. Известно, что гауссов пучок задается конфокальным параметром R э и положением плоскости перетяжки. Эти величины определяются конфигурацией ре-зонатора лазера:
| ( | 2) | |||||||||
| R ý=2 L | g g | 1− g g | , | (2.1) | ||||||
| (g 1+ g 2−2 g 1 g 2) |

где g 1 и g 2 – обобщенные параметры резонатора, которые рассчитыва-ются по формулам:
g 1=1− L; g 2=1− L,
 |  |
r 1 r 2
где L – длина резонатора; r 1 и r 2 – радиусы кривизны зеркал резонатора, причем r 1(r 2) берется положительным, когда зеркало обращено вогнуто-стью внутрь резонатора.
Положение плоскости перетяжки (плоскости наименьшего сече-ния) рассчитывается по формулам:
| Z | = L | [ g 2(1− g 1] | ; Z | = L | [ g 1(1− g 2 | ] | , | (2.2) | |||||
| (g 1 | + g 2−2 g 1 g 2) | (g 1 | + g 2−2 g 1 g 2) | ||||||||||
где Z 1 и Z 2 – расстояние от соответствующего зеркала до плоскости пе-ретяжки.
Необходимо иметь в виду, что формулы (2.1) и (2.2) справедливы для резонаторов произвольной конфигурации, свойства которых опи-сываются с помощью теории эквивалентного конфокального резонато-ра (ЭКР). Если параметры резонатора неизвестны, но пучок является
Э и Zi можно найти по известным диаметру
и расходимости пучка. Если диаметр пучка и расходимость излучения измерены по спаду интенсивности в е 2 раз, то они связаны с R Э какгауссовым,товеличины R
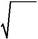
| D =2 | λ R ý | ; | (2.3) | |||||
| 2π | ||||||||
| 2 =2 | 2λ | . | (2.4) | |||||
| π R ý |
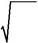
По формуле (2,3) определяется диаметр пучка в плоскости пере-тяжки. На расстоянии Z от плоскости перетяжки диаметр пучка равен:

| D = D 1+ 2 | , | (2.5) | |||||
| Z | |||||||
| где ζ = | 2 Z | – относительная продольная координата. | |||||
| R Ý |
С помощью формулы (2.4) по известному значению расходимости
θ можно найти R Э, а затем, пользуясь формулами (2.3) и (2.5), опреде-лить положение плоскости перетяжки относительно того сечения пуч-ка, в котором известна величина диаметра пучка. Если величины D 0, Dz и θ неизвестны, их можно определить экспериментально. Что касается
положения плоскости перетяжки, то иногда нахождение Z облегчается вследствие того, что перетяжка всегда располагается на плоском зерка-ле резонатора (форм. 2.2). Наконец, если θ и D известны или измерены не по уровню 1/ е 2 или они определены по доле энергии в сечении пучка или телесном угле, необходимо сначала сделать пересчет по формулам (1.2)–(1.4), а затем воспользоваться формулами (2.3)–(2.5).
Итак, будем считать, что пучок, падающий на линзу, задан. Не оста-навливаясь здесь на доказательстве, примем, что пучок за линзой оста-ется гауссовым. Следовательно, его тоже можно характеризовать кон-фокальным параметром и положением плоскости перетяжки. Как это принято в оптике, будем обозначать их теми же буквами, но со штри-хами. Кроме того, обозначим расстояние от линзы до перетяжки пучка через d, причем d будем отсчитывать от линзы, поэтому, если перетяжка расположена слева от линзы, d будет иметь отрицательное значение. Ус-ловия задачи даны на рис. 2.2.
Задача заключается в том, чтобы определить R ′ и dʹ за линзой. По-
Ý
нятно, что определив R ′ и dʹ, мы сможем найти все параметры пучка,
Ý
т.е. полностью характеризовать пучок. Воспользуемся фундаменталь-ным свойством гауссова пучка, которое заключается в том, что, если
в каком-либо сечении пучка известны радиус кривизны волнового фронта и диаметр пучка, то им соответствует только одно значение R Э и положение плоскости перетяжки этого пучка. Действительно, если исключить Z из выражения для радиуса кривизны волнового фронта
| R | = | 1+ 2 | R ý, | (2.6) | |||
| 2ζ | |||||||
и выражения (2.5), получим
HH ʹ

| R | ʹ | ||
| R | |||
| ‒ | |||
| 2 W | 2 W 0ʹ | ||
| ‒ d | d ʹ |
Рис. 2.2. Преобразование гауссова пучка тонкой положительной линзой
| R ý= | 4 kW 2 R 2 | , | (2.7) | ||||||
| + 4 R | ) | ||||||||
| (k W | |||||||||
| где | W –радиус пучка: | W = D /2; | |||||||
| k = | 2π | – волновое число. | |||||||
| λ | |||||||||
Подставляя в (2.5) значение R Э,полученное из(2.6),и решаяполученное уравнение относи-тельно Z, найдем:
| Z = | k 2 W 4 R | . | (2.8) | |||
| + 4 R | ) | |||||
| (k W |
Знак Z в (2.8) определяется знаком R, т.е. перетяжка расположена относительно сечения, в котором определяются R и W, в той стороне, куда обращена вогнутость волнового фронта.
Параметры Wʹ и Rʹ преобразованного линзой пучка легко опреде-ляются в сечении, где установлена линза. Действительно, в плоскости линзы W = Wʹ, W можно найти по формуле (2.5) для падающего на линзу пучка, приняв Z = d. Радиус кривизны волнового фронта пучка в пло-
| скости линзы определяется формулой Гаусса | − | = | , где R нахо- | ||||
| R ′ | R | f ′ | |||||
дится по формуле (2.6), в ней также Z = d. Подставляя найденные таким образом R ʹ и W в (2.7), получим выражение для конфокального параме-тра преобразованного линзой пучка:
| R ý′= | R ý | . | (2.9) | |||||||||
| d | R ý | |||||||||||
| 1+ | + | |||||||||||
| f ′ | 2 f ′ | |||||||||||
Производя аналогичные действия с помощью формулы (2.8), мож-но найти положение плоскости перетяжки пучка за линзой:
| 1+ | d | |||||||||||||||
| d ′ | ||||||||||||||||
| 1− | = | f ′ | . | (2.10) | ||||||||||||
| f ′ | d | R ý | ||||||||||||||
| 1+ | + | |||||||||||||||
| 2 f | ||||||||||||||||
| f ′ | ′ | |||||||||||||||
В формулах (2.9) и (2.10) знаки у d и f ʹ выбираются в соответствии
с правилами геометрической оптики, величина R Э является сугубо по-ложительной. Эти выражения справедливы и для линзы конечной тол-щины, если отсчитывать расстояния d и dʹ от соответствующих главных плоскостей линзы. Действительно, ход рассуждений, принятый при выводе формулы (2.9) и (2.10), в этом случае не нарушается. Формула Гаусса остается справедливой и для линзы конечной толщины, а допу-щение о том, что размер пятна на линзе не изменяется, остается в силе, поскольку увеличение в главных плоскостях линзы равно единице. Ска-занное можно отнести и к сложному компоненту, например, объективу, состоящему из нескольких линз.
Формулы (2.9) и (2.10) можно использовать и в случае многомодо-вого пучка. Известно, что радиусы кривизны волновых фронтов всех мод одинаковы, и, следовательно, плоскость перетяжки у них одна и та же. Поэтому формула (2.10) определяет положение плоскости пере-тяжки независимо от модового состава излучения. Соотношение между размером пучка одномодового и многомодового излучения (коэффици-ент мод) остается прежним и за оптической системой. Поэтому, рас-
считав с помощью формулы (2.9) конфокальный параметр пучка R ′ ,
Ý
можно найти поперечные размеры пучка и его угловую расходимость как произведение соответствующих параметров одномодового пучка, определенных по формулам (2.3)–(2.5), на коэффициент мод.
Оптическая система преобразует многомодовое излучение так же, как и одномодовое, но поперечные размеры пучка многомодового излу-чения в любой плоскости будут в соответствующее число раз больше; во столько же раз будет больше и расходимость пучка. Это обстоятель-ство необходимо принимать во внимание при расчете световых диаме-тров компонентов.
Параметры лазерного пучка за оптической системой можно рас-считать с помощью формул геометрической оптики, принимая сечение пучка до линзы за «предмет» и находя его изображение в сопряженной плоскости за линзой. Однако такой расчет является неудобным и гро-моздким. Кроме того, следует иметь в виду, что перетяжку и ее изобра-жение за оптической системой нельзя рассматривать как предмет и его изображение в геометрической оптике. Например, из геометрической оптики вытекает, что изображение предмета, находящегося в передней фокальной плоскости линзы, находится в бесконечности, а из форму-лы (2.10) следует, что, если перетяжка падающего на линзу пучка на-ходится в передней фокальной плоскости, то перетяжка пучка за линзой находится в ее задней фокальной плоскости. Такое же несоответствие получается и для поперечного увеличения.
Это несоответствие вытекает из того, что гауссов пучок не является гомоцентрическим, и центр кривизны волнового фронта падающего на линзу пучка не совпадает с плоскостью перетяжки (2.6). Однако если оптическая система находится достаточно далеко от плоскости пере-тяжки (в дальней зоне), формулы лазерной оптики (2.9) и (2.10) перехо-дят в формулы геометрической оптики. В этом случае R = Z, т.е. гауссов пучок можно рассматривать как гомоцентрический. В этом случае чле-
ном (R Э/2 f ʹ )2 в знаменателях формул (2.9) и (2.10) можно пренебречь по сравнению с (1+ d / f ʹ )2. Формула (2.10) превращается в формулу Гаусса
d 1′ − d 1 = f 1′, а из формулы (2.9) следует, что увеличения (поперечное и
 |  |  |
угловое) для лазерной и геометрической оптики являются одинаковыми. Формулы (2.9) и (2.10) являются основными для габаритного рас-чета оптических систем для формирования гауссова пучка. Добавим к
ним еще некоторые положения, которые примем без доказательства. Если отсчитывать от плоскости линзы расстояния Z до сечений
пучка, который распространяется в отсутствии линзы, и расстояния l до сечений пучка, который образуется линзой, то в плоскостях, связанных между собой соотношением (рис. 2.3)
| = | + | , | (2.11) | ||||
| l | z | f ′ | |||||
картина распределения одинакова, а масштаб равен M = ( f ′+ z ). f ′
Из (2.11) видно, что за линзой от 0 до f ʹ отображаются все сечения пучка от 0 до ∞. За фокальной плоскостью положительной линзы в об-ласти f ʹ < l < ∞ отображаются плоскости ∞< f ʹ < l.
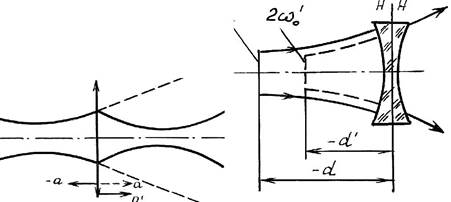
Как видно из формулы (2.10), если расходящийся гауссов пучок пада-ет на отрицательную линзу, то за линзой он продолжает расходиться, а пе-ретяжка получается мнимой (dʹ имеет отрицательное значение) (рис. 2.4).
| Применительно к отрицатель- | H H' | ||||||||||
| ной линзе: | 2ω | ||||||||||
| Z | 2ω0ʹ | ||||||||||
| l = Z + | . | ||||||||||
| ( | f | − Z) | |||||||||
| HH ʹ | |||||||||||
| ‒ d ʹ | |||||||||||
| ‒ a | a | ‒ d | |||||||||
| a ʹ | Рис. 2.4. Преобразование гауссова | ||||||||||
| Рис. 2.3. К формуле (2.11) | пучка отрицательной линзой |
При изменении Z от 0 до | f | l пробегает все значения от 0 до ∞, а плоскости Z > | f | и Z < 0 не отображаются отрицательной линзой нигде. Рассмотрим, как используются полученные соотношения для выбора и расчета оптических систем.