МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)
Кафедра №603
«Прочность авиационных и ракетно-космических конструкций»
ЧИСЛЕННЫЕ МЕТОДЫ
Краткое методическое пособие
МОСКВА – 2013
ВВЕДЕНИЕ
Создание новых и модернизация существующих технических, технологических, экономических и прочих объектов невозможно без детального исследования их поведения в реальных условиях. Существуют два подхода к такому исследованию. Первый из них заключается в создании реального образца объекта с последующим его экспериментальным изучением. Второй обычно применяют там, где нельзя провести весь комплекс исследований на самом объекте вследствие сложности его изготовления, выполнения требуемых измерений или значительных затрат на постановку необходимых экспериментов. Он состоит в применении специальных приёмов, называемых методами моделирования.
Методы моделирования основаны на понятии подобия различных объектов. При этом подобными называют объекты, параметры которых, определяющие их состояние, отличаются от исходных в заранее известное число раз, называемое масштабом подобия. Один из двух объектов, между которыми существует подобие, можно назвать объектом моделирования, а другой – его моделью. Подобие объектов может использоваться как при физическом, так и при математическом моделировании.
Физическое моделирование заключается в постановке экспериментов, как правило, с уменьшенной моделью объекта, несущей в себе все его исследуемые особенности. При этом круг исследований и их сложность не изменяются, как если бы все исследования проводились на самом объекте. Математическое моделирование основано на том, что реальные процессы, протекающие в объекте моделирования и характеризующие его свойства, могут быть описаны определенными математическими соотношениями. Совокупность математических соотношений, позволяющих описать исследуемые свойства объекта, называют его математической моделью.
Построение математической модели начинают с формализованного описания объекта, в которое включают процессы, наиболее существенные для задачи моделирования. Каждый из выбранных процессов описывается в форме тех или иных уравнений, что позволяет при последующем объединении этих уравнений в систему относительно общих параметров получить математическую модель исследуемого объекта.
Такая математическая модель сама по себе ещё не дает возможности судить о поведении объекта моделирования. Исследование моделирующей системы математических уравнений позволяет сделать лишь ряд качественных выводов о поведении объекта, исходя из их общего вида, да и то лишь в относительно простых случаях. Поэтому для изучения свойств объекта по его математическому описанию нужно решить систему уравнений, составляющую это описание, и получить результаты, аналогичные измерениям на физической модели. Другими словами, необходим алгоритм решения системы уравнений математической модели, который позволит осуществить собственно процесс моделирования.
Математическое описание реальных объектов представляет собой достаточно сложные системы уравнений. Поэтому математическое моделирование практически возможно только при использовании вычислительных машин.
Данное краткое методическое пособие по выполнению лабораторных работ имеет целью ознакомление с численными методами, используемыми для разрешения систем уравнений, составляющих математическую модель исследуемого объекта, и получение навыков их применения при решении инженерных задач.
Для более подробного знакомства с теоретическими основами рассмотренных методов следует воспользоваться книгами, представленными в приведенном ниже списке литературы.
СПИСОК ЛИТЕРАТУРЫ
1. Мудров А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП "РАСКО", 1991. 272 с.
2. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение: Пер. с англ.-М.: Мир, 1998.575 с.
3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – 3-е изд., перераб. и доп. М.: БИНОМ. Лаборатория знаний, 2003. 632 с.
4. Воеводин В.А. Вычислительные основы линейной алгебры. М.: Наука, 1977. 303 с.
5. Волков Е.А. Численные методы. М.: Наука, 1982. 254 с.
6. Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах. М.: Высшая школа, 2004. 480 с.
7. Инженерные расчеты на ЭВМ: Справочное пособие. Под ред. В.А.Троицкого. Л.: Машиностроение, 1979. 288 с.
Глава 1. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
При решении реальных инженерных задач возникают ситуации, когда аналитическое вычисление определенного интеграла затруднено или невозможно. В подобных ситуациях решение может быть получено одним из методов приближенного вычисления значения определенного интеграла.
Все методы приближенного вычисления определенных интегралов основаны на геометрическом смысле интеграла Ньютона-Лейбница. Он заключается в том, что определенный интеграл
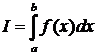
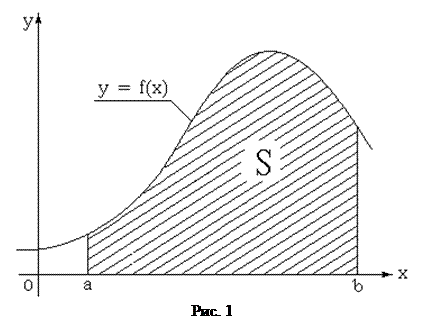численно равен площади S криволинейной трапеции, ограниченной графиком подинтегральной функции f(x) и осью абсцисс на отрезке [a, b], как показано на рис.1.
Поэтому для приближенного вычисления определенного интеграла достаточно подсчитать площадь трапеции S. Можно указать множество способов вычисления площади S. Простейшие из них - методпрямоугольников, методтрапеций и метод Симпсона.
Метод прямоугольников
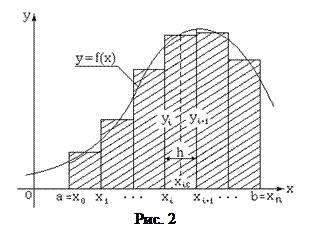
В методе прямоугольников криволинейная трапеция аппроксимируется набором прямоугольников, как показано на рис.2. В этом случае площадь криволинейной трапеции представляется в виде суммы площадей этих прямоугольников, а интеграл I приближенно вычисляться по формуле
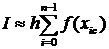
или в развернутом виде
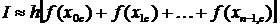
где x iс= (x i + x i+1 ) / 2 - абсцисса центральной точки i -го участка разбиения [a, b]; h =(b - a) / n - шаг равномерного разбиения отрезка; n - количество участков разбиения.
Метод трапеций
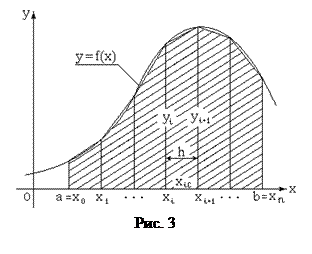Аналогично вычисляется определенный интеграл по методу трапеций, где площадь криволинейной трапеции S заменяется суммой площадей элементарных трапеций (см. рис.3). Такой подход приводит к вычислению определенного интеграла I по формуле
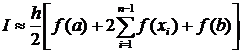
или, раскрывая сумму:
.
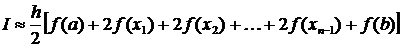Метод Симпсона (J.Gregory(Грегори) 1668, Th.Simpson 1743)
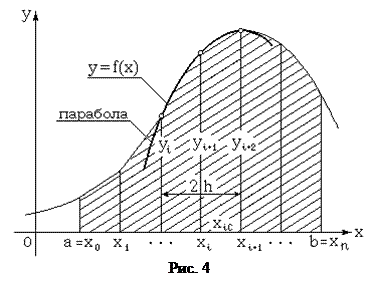В методе Симпсона площадь криволинейной трапеции рассчитывается как сумма площадей ряда криволинейных трапеций, у которых криволинейная сторона представляет собой участок параболы. Это можно видеть на рис.4. Каждая парабола может быть проведена только через три граничные точки, принадлежащие двум соседним отрезкам. Поэтому число участков разбиения отрезка [a, b] в отличие от предыдущих методов обязательно должно быть четным. Исходя из этого, определенный интеграл приближенно вычисляется по формуле:
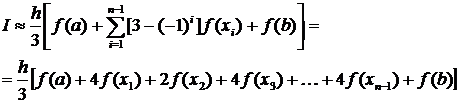
Точность вычисления интеграла определяется погрешностью, которая может быть абсолютной или относительной. Абсолютная погрешность есть модуль разницы между точным значением интеграла и его приближенным значением, полученным выбранным численным методом при конкретном количестве участков разбиения отрезка [a, b], или, что то же самое, при конкретном шаге интегрирования:
.
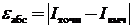Относительная погрешность является более информативным параметром точности вычисления значения интеграла, поскольку показывает погрешность в долях точного значения. Она вычисляется как модуль отношения разницы между точным и вычисленным значениями интеграла к его точному значению:
.
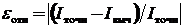На практике, когда точное значение интеграла неизвестно, в качестве абсолютной и относительной погрешностей условно используют следующие из теории рядов величины:
, 
,
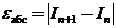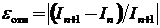где нижний индекс n соответствует количеству участков разбиения отрезка [a, b].
Точность вычисления определенного интеграла приближенными методами зависит от двух основных факторов: величины шага h разбиения отрезка [a, b] и формы представления геометрического элемента, используемого при вычислении площади - прямоугольник, трапеция, криволинейная трапеция с параболической стороной.
С одной стороны точность вычисления интеграла может быть повышена путем увеличения точности аппроксимации подынтегральной функции. Например, при одинаковом шаге точность метода Симпсона выше, чем у метода трапеций и метода прямоугольников, поскольку в нем применяется квадратичная аппроксимация подынтегральной функции, а не линейная.
С другой стороны точность вычисления интеграла увеличивается c уменьшением шага h. Однако, этот способ уменьшения погрешности можно применять лишь до определенного предела. Причиной этого является параллельный рост ошибок округления выполняемых вычислений, который сводит на нет уменьшение погрешности.