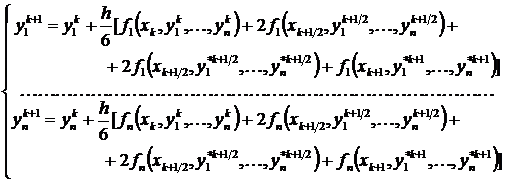И УРАВНЕНИЙ ВЫСШИХ ПОРЯДКОВ

Задача Коши для нормальной системы обыкновенных дифференциальных уравнений записывается в виде

,

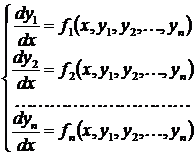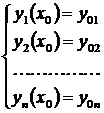
или в матричной форме следующим образом

, ,

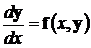где

, , .

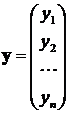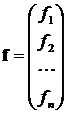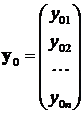Система дифференциальных уравнений связывает независимую переменную x, искомые функции y ₁, y ₂ ,..., y_n и их первые производные. В данном случае решение задачи Коши заключается в отыскании функций y ₁ = y ₁ (x), y ₂ = y ₂ (x),..., y_n = y_n(x), обращающих каждое уравнение системы в тождество на конечном или бесконечном интервале (a, b) и удовлетворяющих начальным условиям.

Такая форма записи задачи Коши является канонической для систем обыкновенных дифференциальных уравнений. К ней могут быть приведены как любые другие формы представления систем дифференциальных уравнений, разрешенных относительно старших производных, так и аналогичные дифференциальные уравнения высших порядков. Приведение дифференциальных уравнений высших порядков к нормальной системе дифференциальных уравнений осуществляется по следующей схеме. Если дана задача Коши следующего вида

,

, , , …, ,

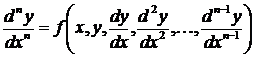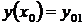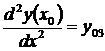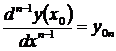то замена

, , , …, ,

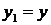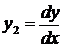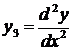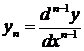приводит ее к

,

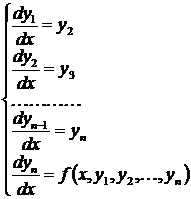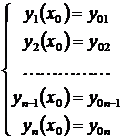
что является задачей Коши для нормальной системы дифференциальных уравнений.

Для решения такой задачи Коши используются те же методы, что для обыкновенных дифференциальных уравнений 1-го порядка. Это обуславливается тем, что матричная форма записи задачи Коши для нормальной системы полностью совпадает с ее формулировкой для этих уравнений. Единственным отличием является то, что вместо функций y(x) и f(x,y) используются вектор-функции y и f, состоящие из n функций y ₁ (x), y ₂ (x),..., y_n(x) и f ₁ (x,y ₁,..., y_n), f ₂ (x,y ₁,..., y_n),..., f_n(x,y ₁,..., y_n), соответственно. При этом расчетные схемы методов и оценки их погрешностей сохраняются.

Метод Эйлера

Соотношения метода Эйлера для нормальной системы в матричной форме имеют вид

,

.

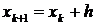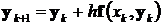или в развернутой форме

, .

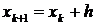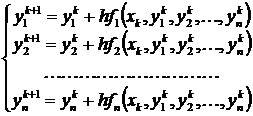Геометрическая интерпретация работы метода Эйлера решения задачи Коши для нормальной системы идентична его геометрической интерпретации для дифференциальных уравнений 1-го порядка. Однако, в данном случае движение осуществляется вдоль некоторойгиперкривойв (n+1) -мерном пространстве переменных x, y ₁, y ₂ ,...,y_n.

Модифицированный метод Эйлера

Основные соотношения усовершенствованного метода Эйлера в матричной форме записываются следующим образом

, ,

, .

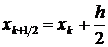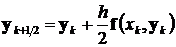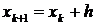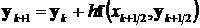что в развернутом виде дает

, .

, .

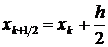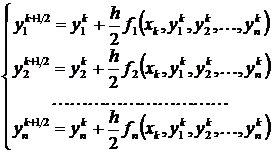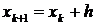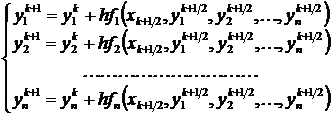Метод Рунге-Кутта

Преобразование соотношений метода Рунге-Кутта 4-го порядка точности на случай решения нормальной системы дифференциальных уравнений в мат­ричной форме приводит к следующему

, ,

,

, ,

.

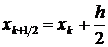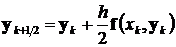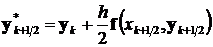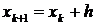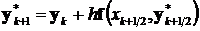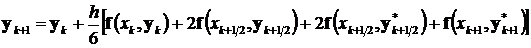Как видно из приведенных соотношений алгоритм метода строится по той же схеме из 4-х шагов, но в (n+1) -мерном пространстве. При этом направ­ление отыскания следующей точки представляет собой вектор, каждая ком­понента которого вычисляется как некоторое осредненное значение танген­са угла между касательной к интегральной гиперкривой и осью аргумента системы x.

В развернутом виде соотношения метода Рунге-Кутта для нормальной системы из n уравнений записываются в виде

, .

, .
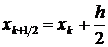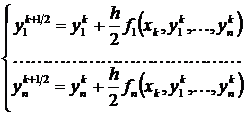
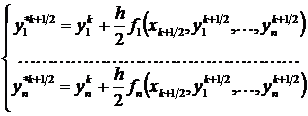
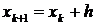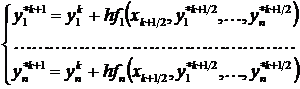