Интерполяцией называется приближение функции, значения которой заданы в виде таблицы, некоторой другой функцией, заданной аналитически, которая совпадает с исходной при табличных значениях аргумента.
Простейшая задача, приводящая к интерполяции функций, заключается в следующем. В дискретные моментывремени x 1, x 2, ..., xn измеряется значение некоторой физической величины y, то есть наблюдается зависимость функции y от аргумента x, и строится таблица
| x | x 1 | x 2 | ... | xn |
| y | y 2 | y 2 | ... | yn |
Требуется восстановить значения функции при любых других значенияхаргумента x из отрезка [ x 1, xn ] или подобрать аналитическое выражение для приближающей функции y(x) достаточно простого вида, значения которой совпадали бы с заданными в таблице
.
Геометрический смысл задачи состоит в том, что через точки, которыми отображаются табличные значения аргумента и функции на поле декартовой системы координат x0y, как это показано на рис.1, и которые называются узловыми точками или узлами интерполяции, необходимо провести по крайней мере непрерывную линию, подобрав для нее аналитическое описание.
В зависимости от требований, которые накладываются на приближающую функцию могут применяться различные формы ее представления: линейная, квадратичная, кубическая или более высокого порядка. К простейшим из них относятся кусочно-линейная интерполяция, интерполяция кубическим сплайном и интерполяция многочленами, в частности, многочленом Лагранжа и другие.
Кусочно-линейная интерполяция
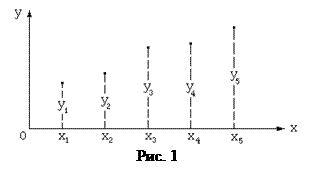
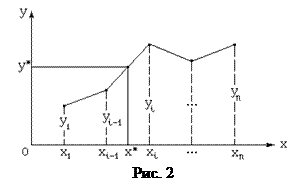Кусочно-линейная интерполяция состоит в представлении таблично заданной функции на каждом отрезке между абсциссами узловых точек линейной зависимостью y = a 1 + a 2 x так, как это показано на рис.2. Коэффициенты a 1 и a 2 определяются для каждого отрезка [ xi -1, xi ] в отдельности из условий
|
|
.
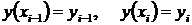В результате приближающая функция является непрерывной, однако ее первая производная оказывается уже кусочно-непрерывной функцией, которая в каждом узле интерполяции имеет точку разрыва первого рода. Это часто накладывает существенные ограничения на ее дальнейшее использование.
Интерполяция кубическим сплайном (I.J.Schoenberg (Шонберг), 1946)
Сплайнами называется широкий класс приближающих функций, конструируемых путем кусочной интерполяции с использованием различных функций, в число которых входят полиномы, в частности, кубический.
Этой зависимостью таблично заданная функция представляется внутри каждого отрезка [ xi, xi+1 ]:
,
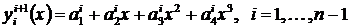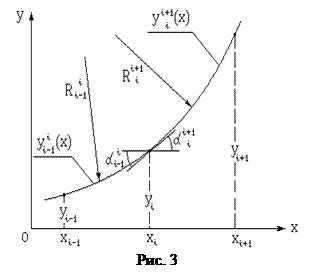
где нижний и верхний индексы указывают на номера узлов, между которыми проведен сплайн (см. рис.3)
Отрезки образуют область определения сплайна. Вычисление коэффициентов сплайна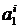 
, 
, 
, 
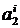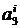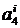осуществляется исходя из следующих условий. По определению, значения сплайна в узловых точках должны совпадать с соответствующими значениями таблично заданной функции
.
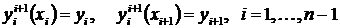Эти условия дают 2(n -1) уравнений для определения коэффициентов сплайна.
Кроме этого, требуется, чтобы полином данного отрезка сопрягался с соседними полиномами, как по углу наклона касательной в узловых точках, так и по радиусу кривизны. Сопряжение по углу наклона соответствует равенству значений первых производных соседних полиномов в каждой узловой точке, а по радиусу - вторых производных. Это дает еще два условия
|
|
, 
, 
.
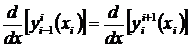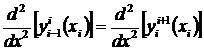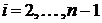Данные условия не применимы для граничных точек x 1 и xn, так как поведение функции за пределами отрезка неизвестно. Тем самым, вместе с приведенными выше соотношениями получены 4(n -1)-2 уравнения, и для полной системы не хватает еще двух уравнений.
С целью построения недостающих уравнений можно задавать в граничных точках значения угла наклона касательной (исходя из физической сути задачи или с помощью интерполяции по 4-м крайним точкам с последующим вычислением производной)
, 
.
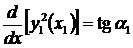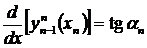Заметим, что возможны и иные способы задания граничных условий. Например, можно задавать граничные значения не первых, а вторых производных:
, 
.
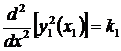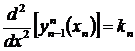Особый способ, называемый условием «нет узла» или «запрет стыка», состоит в приравнивании третьих производных полиномов на стыке двух крайних отрезков:
, 
.
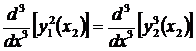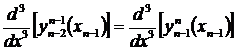Перечисленные условия дают систему из 4(n -1) линейных алгебраических уравнений, позволяющую вычислить коэффициенты для каждого отрезка сплайна. Полученная функция будет непрерывной и гладкой вместе со своей первой производной, а ее вторая производная - непрерывной.
Многочлен Лагранжа (J.L.Lagrange, 1795)
Представляет собой частный случай, когда приближающая функция ищется в виде линейной комбинации базисных функций jk(x). Они должны быть определены для всего отрезка интерполяции [ x 1, xn ], линейно независимы, и их количество должно быть равно числу узлов таблично заданной функции
.
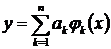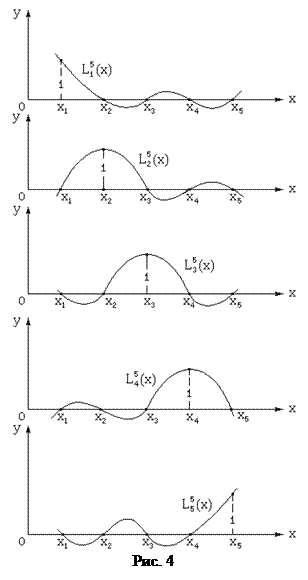Коэффициенты a 1, a 2,..., an определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента. Использование этих условий сводит задачу к системе n линейных алгебраических уравнений относительно a 1, a 2,..., an. В многочлене Лагранжа в качестве функций jk(x) используются полиномы (n-1) степени
|
|
,
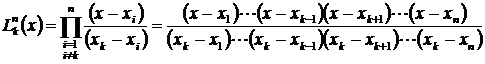которые для пяти узловых точек записываются в виде
,
…………………………………………………
.
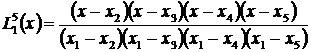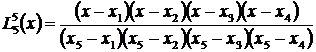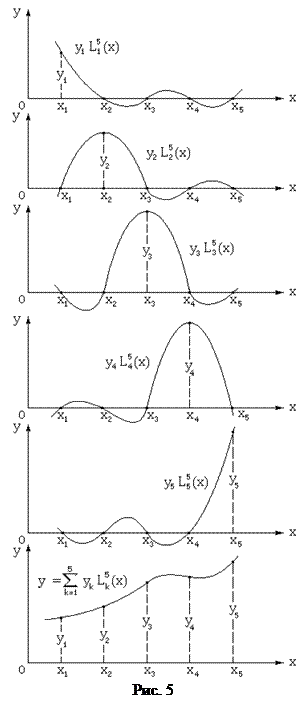
Графики этих полиномов представлены на рис.4. Для каждого полинома характерно то, что для всех значений xi узловых точек он принимает нулевые значения, кроме k -ой, где его значение равно единице.
При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции
.
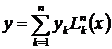Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.5.