Обыкновенное дифференциальное уравнение 1-го порядка
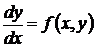
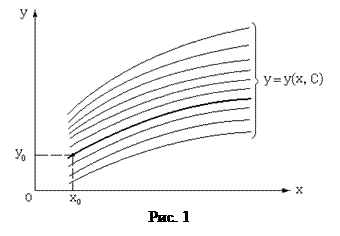
связывает независимую переменную x,искомую функцию y и ее производную. Решение дифференциальногоуравнениязаключается в отысканиифункции y = y(x), обращающей это уравнение в тождество на конечном или бесконечном интервале (a, b). Различают общее и частные решения дифференциального уравнения. Общее решение имеет вид y = y(x, C), где C - произвольная постоянная интегрирования. Его графическим отображением является семейство кривых (см. рис.1), называемых интегральными. Каждая интегральная кривая является отображением частного решения, соответствующего своему значению постоянной C. Для выделения частного решения из множества общего решения необходимо задать начальное условие
.
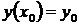Такая постановка задачи решения дифференциальных уравнений называется задачей Коши (A.L.Cauchy, 1789-1857).
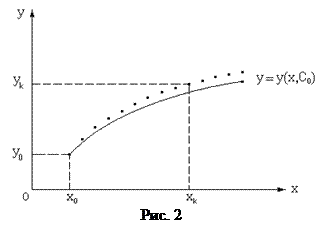Для решения задачи Коши существует множество методов, которые делятся на одношаговые и многошаговые. Все они позволяют получить искомое решение в виде таблично заданной функции, в той или иной мере согласующееся с истинным частным решением (см. рис.2). Эти группы методов различаются объемом информации, которая используется для вычисления координат очередной точки табличной функции. Одношаговые методы используют значения функции и ее производной только в одной предыдущей точке, в то время как многошаговые - в нескольких. К одношаговым методам решения задачи Коши относятся метод Эйлера, модифицированный метод Эйлера, методы Рунге-Кутта и другие.
Метод Эйлера (L.Euler, 1768)
Он является старейшим методом решения задачи Коши и заключается в последовательном применении следующих формул
,
,
,
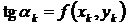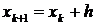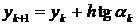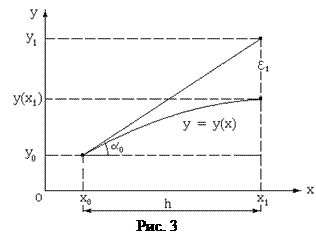геометрическая интерпретация которых представлена на рис.3. В точке x 0 вычисляется значение производной dy/dx через f(x,y), которое определяет угол наклона касательной к графику точного решения задачи Коши. Следующая точка численного решения определяется как точка на этой касательной с абсциссой x 1 = x 0 + h. В компактном виде эти соотношения записываются следующим образом
,
.
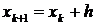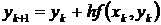Метод Эйлера - самый простой метод численного интегрирования. Он относится к методам первого порядка точности, поскольку его решение совпадает с истинным только в том случае, когда истинное решение является линейной функцией y = a 1 + a 2 x. Его погрешность ek на каждом шаге пропорциональна величине h 2. Это обусловлено тем, что в качестве направления, определяющего положение следующей точки численного решения, используется касательная в крайней левой точке каждого отрезка [x k ,x k+1 ]. Из рис.3 видно, что для получения более точного численного решения надо использовать некоторое промежуточное направление между направлениями касательных в крайних точках рассматриваемого отрезка.
Модифицированный метод Эйлера
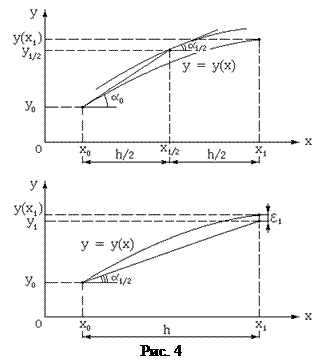Этот метод является методом второго порядка точности. Его погрешность ek на каждом шаге пропорциональна величине h 3, а решение совпадает с истинным в случае, когда оно представимо квадратичной функцией y = a 1 + a 2 x + a 3 x 2. Характерной особенностью метода является использование в качестве направления поиска каждой последующей точки численного решения касательной, определяемой в центре отрезка [x k, x k+1 ]. Как видно из рис.4, последовательно выполняются два шага по методу Эйлера.
Первый из них используется для вычисления тангенса угла наклона касательной в срединной точке
,
,
,
,
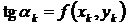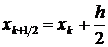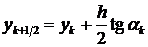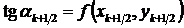а второй - для вычисления новой точки
,
.
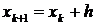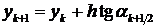Если тангенсы углов наклона заменить на правую часть дифференциального уравнения f(x,y), то вышеприведенные формулы для выполнения одного шага по усовершенствованному методу Эйлера сведутся к следующим
, 
,
, 
.
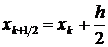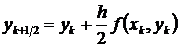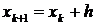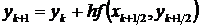Усовершенствованный метод Эйлера дает большую точность решения, чем метод Эйлера. Однако это достигается тем, что его трудоемкость увеличивается примерно в два раза, поскольку для одного шага приходится два раза вычислять значение правой части дифференциального уравнения.
Метод Рунге-Кутта (C.Runge 1895, W.Kutta 1901)
Под наименованием «метод Рунге-Кутта» принято подразумевать целое семейство методов численного решения задачи Коши, объединенных одной идеей выбора некоторого усредненного направления поиска каждой новой точки. Остановимся только на одном из них: методе Рунге-Кутта 4-го порядка точности.
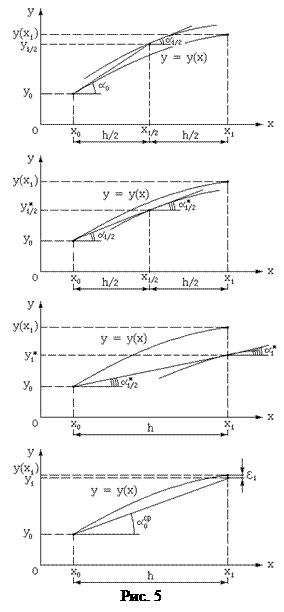Алгоритм метода строится по следующей схеме. Из начальной точки, как это можно видеть на рис.5, в направлении касательной делается шаг по методу Эйлера на величину h/2 и в полученной точке вычисляется тангенс угла наклона касательной:
,
,
,
.
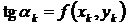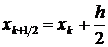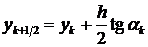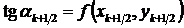Из начальной точки по найденному направлению делается второй шаг на ту же величину и определяется тангенс угла наклона во второй средней точке
,
.
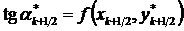Третий шаг делается опять из начальной точки по последнему найденному направлению (a *k+1/2 ), но на шаг h, где опять находится тангенс угла наклона касательной
,
,
.
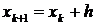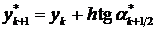Последний шаг из начальной точки на величину h делается по присущему этому методу осредненному направлению и находится ордината следующей точки численного решения
,
,
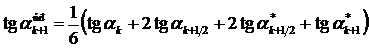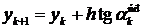Описанные действия, необходимые для получения координат каждой последующей точки численного решения, реализуются в виде следующей последовательности вычислений по формулам
, ,
,
, 
,
.
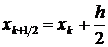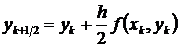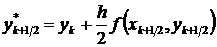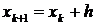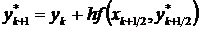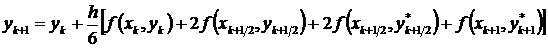Получающееся численное решение имеет на каждом шаге h погрешность ek, которая пропорциональнавеличине h 5, оно совпадает с истинным в случае, когда оно есть многочлен четвертого порядка y = a 1 + a 2 x + + a 3 x 2 + a 4 x 3 + a 5 x 4.