Заочная физико-математическая школа
МАТЕМАТИКА
ЗАДАНИЕ № 1
Класс
Текстовые задачи
Для математического исследования процессов и явлений, реально происходящих в действительности, надо суметь описать их на языке математики, т.е. построить математическую модель процесса, явления.
Математическими моделями принято называть системы математических соотношений, описывающих изучаемый процесс или явление.
Составление математической модели задачи, перевод задачи на математический язык осуществляется, прежде всего, при решении текстовых задач. При этом используются их алгебраические и аналитические модели. Такой моделью может быть функция, описывающая явление и процесс, уравнение, система уравнений, неравенство, система неравенств, система уравнений и неравенств и др.
При составлении модели текстовая задача переводится на язык алгебры или начал анализа.
Общая схема решения задач с помощью алгебраической модели состоит в следующем:
1. Выбор и обозначение переменных для составления модели. (При этом буквенных обозначений можно вводить много, лишние уйдут при преобразованиях).
2. Выражение остальных переменных через выбранные и заданные в задаче фиксированные значения величин.
3. Составление из полученных выражений уравнений, неравенств, их различных систем, исходя из текста задачи (это и есть этап составления алгебраической модели).
4. Исследование (реализация) модели методами алгебры (решение уравнения, неравенства, их системы и т.д.).
5. Исследование полученного результата в соответствии с условиями задачи.
Переменные (неизвестные) в модели следует выбирать так, чтобы проще составлялось и проще решалось уравнение.
В связи с этим необходимо выполнить простейший анализ содержания задачи. Во-первых, выяснить, о каких величинах идет речь, выделить среди них переменные и постоянные. Любая из переменных величин может быть принята за переменную алгебраической модели. Если она не одна, то и уравнений (т.е. алгебраических моделей) может быть составлено не одно.
Во-вторых, нужно проанализировать процесс, описанный в задаче, чтобы составить для решения задачи наиболее простое уравнение. Ведь одна и та же задача может быть нередко решена с помощью различных уравнений, неравенств, их систем. Полезно время от времени составить несколько разных уравнений, оценить сложность их решения, выбрать такое, которое решается проще.
Задачи на проценты
Здесь важно знать следующее: (r % от числа x) = 
.
Число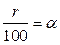 
называется долей или удельным процентом.
Если исходное число x увеличивается на долю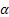 
(на r %), то новое число станет равным x 1 = x+ 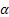x = x (1+ 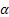), т.е. увеличится в (1+ 
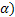раз.
Если новое число x 1 снова увеличивается на долю 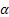, то получим число x 2 = x 1(1+ 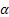) = x (1+ 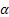)2. Если этот процесс повторяется n раз, то получим число xn = x (1+ 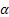) n – формула сложных процентов.
Если исходное число x уменьшается на долю 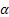(на r %), то новое число станет равным x 1 = x- 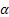x = x (1- ).
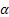Пример 1. Цену на товар в магазине повысили (понизили) на 30%, а затем новую цену снова повысили (понизили) на 50%. На сколько процентов в итоге повысилась (понизилась) цена?
Решение. Пусть x – первоначальная цена товара. Тогда после двух повышений цена станет равной x 2 = x (1 + 0,3)(1 + 0,5) = 1,95 x = x+ 0,95 x, т.е. цена увеличится на 95%.
После двух понижений цена станет равной x 2 = x (1 - 0,3)(1 - 0,5) = 0,35 x = x - 0,65 x, т.е. цена уменьшится на 65%.
Пример 2. Зарплату понизили на 20%. На сколько процентов нужно повысить новую зарплату, чтобы она сравнялась с первоначальной зарплатой?
Решение. Пусть x – первоначальная зарплата,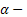 
искомая доля повышения. Составим уравнение, отвечающее условию задачи: x (1 - 0,2)(1 + 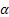) = x. Из этого уравнения находим, что 
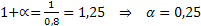, т.е. зарплату следует увеличить на 25%.
Ответ: 25%.
Пример 3. Арбуз дешевле дыни на 75%. На сколько процентов дыня дороже арбуза?
Решение. Здесь важно понять, что с чем сравнивается. Чтобы узнать цену арбуза, нужно знать цену дыни, поэтому за d обозначимцену дыни. Тогда цена арбуза 
Разница в цене равна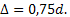 
Чтобы узнать, на сколько процентов дыня дороже арбуза, нужно разницу поделить на цену арбуза: 
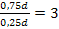. Таким образом, дыня дороже арбуза на 300% или в 4 раза (
).
Ответ: 300%.
Пример 4. В школьной газете сообщается, что процент учеников класса, повысивших успеваемость, заключен в пределах от 2,9% до 3,1%. Найти минимально возможное число учеников в классе.
Решение. Пусть в классе было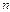 
учеников, из них 
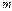- повысили свою успеваемость. Тогда процент учеников, повысивших успеваемость составляет 
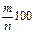, и по условию задачи 
. Заметим, что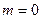 
не удовлетворяет неравенству, и поэтому 
, тогда 
. Итак, самое малое значение 
, которое возможно, равно 33. Проверим, что пара натуральных чисел 
, 
удовлетворяет неравенству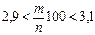 
. Действительно, неравенство выполнено, так как 
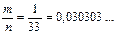и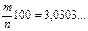 
. Итак, минимально возможное число учащихся в классе: 33.
Ответ: 33.
Задачи на смеси и сплавы
Основное правило решения задач на смеси и сплавы гласит:
«приравниваем чистое вещество».
Пример 5. При смешивании двух растворов одной и той же кислоты с концентрациями 40% и 70% соответственно получили раствор, содержащий 60% кислоты. В каком отношении были взяты первый и второй растворы?
Решение. Пусть x – количество первого раствора, а y - количество второго раствора. Тогда в первом растворе 0,4 x чистой кислоты, а во втором 0,7 x чистой кислоты. А в их смеси 0,6 (x+y) чистой кислоты. Приравнивая чистое вещество, получим уравнение:
0,4 x+ 0,7 y = 0,6 (x+y), из которого находим, что 0,1 y = 0,2 x. Отсюда 
. Ответ: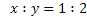 
.
Пример 6. Влажность свежих грибов 90%, а сухих – 15%. Сколько сухих грибов получится из 1,7 кг свежих?
Решение. Пусть x (кг) – количество сухих грибов. Тогда количество «совсем» сухого вещества в свежих грибах равно 0,1 
1,7 = 0,17 (кг), а количество «совсем» сухого вещества в сухих грибах равно 0,85 x (кг). Приравнивая сухое вещество, получим: 0,85 x = 0,17. Откуда x = 0,2 (кг).
Ответ: 0,2 (кг).
Пример 7. Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20%?
Решение. Пусть x (г) – количество воды, которое нужно добавить. Тогда чистого сахара в неразбавленном сиропе будет 0,25 180 = 45 (г), а в разбавленном: 0,2(180 + x). Приравнивая, получим уравнение
0,2 x + 36 = 45, из которого найдем x = 45 (г).
Ответ: 45 (г).
Пример 8. В куске сплава меди с цинком количество меди увеличили на 60%, а количество цинка уменьшили на 40%. В результате общая масса куска сплава увеличилась на 50%. Определите процентное содержание цинка в новом куске сплава.
Решение. Пусть x – количество меди в первоначальном куске, а y – количество цинка в первоначальном куске. Тогда в новом куске меди стало 1,6 x, а цинка стало 0,6 y. Общая масса 1,6 x + 0,6 y = 1,5 (x + y). Из этого уравнения находим, что 0,1 x = 0,9 y или x = 9 y. Тогда общая масса нового сплава будет равна 1,6 9 y + 0,6 y = 15 y, а цинка в нем 0,6 y. Процентное содержание цинка в новом куске сплава равно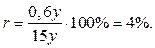 
Ответ: 4%.