Таблица 16
Величины R=R/l в зависимости от T=QT/mnl2 и q=2ngl/Q
| R | Т при различных значениях q | |||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 1 1,0 | l.l | 1.2 | 1,3 | 1.4 | 1,5 | ||||
| 5,75 | 5,25 | 4,84 | 4,47 | 4,19 | 3,91 | 3,69 | 3,47 | 3,28 | 3,12 | 2,97 | 2,83 | 2,72 | 2,59 | 2,50 | 2,39 | |
| 16,46 | 14,38 | 12,78 | 11,53 | 10,50 | 9,66 | 8,94 | 8,31 | 7,78 | 7,31 | 6,91 | 6,53 | 6,20 | 5,91 | 5,62 | 5,38 | |
| 33,00 | 27,44 | 23,59 | 20,75 | 18,53 | 16,78 | 15,31 | 14,13 | 13,09 | 12,22 | 11,44 | 10,77 | 10,16 | 9,62 | 9,16 | 8,72 | |
| 55,56 | 44,03 | 36,72 | 31,59 | 27,78 | 24,84 | 22,47 | 20,53 | 18,91 | 17,55 | 16,34 | 15,31 | 14,41 | 13,61 | 12,89 | 12.2Е | |
| 84,31 | 63,75 | 51,69 | 43,69 | 37,94 | 33,56 | 30,14 | 27,38 | 25,08 | 23,16 | 21,50 | 20,08 | 18,84 | 17,75 | 16,78 | 15,91 | |
| 119,3 | 86,19 | 68,25 | 56,78 | 48,75 | 42,81 | 38,19 | 34,50 | 31,50 | 28,97 | 26,83 | 25,00 | 23,39 | 22,00 | 20,75 | 19,64 | |
| , 160,4 | 111,0 | 86,03 | 70,65 | to, is | 52,44 | 46,53 | 41,88 | 38,08 | 34,94 | 32,28 | 30,00 | 28,03 | 26,31 | 24,80 | 23,44 | |
| 207,8 | 138,0 | 104,9 | 85,19 | 71,94 | 62,38 | 55,13 | 49,41 | 44,81 | 41,02 | 37,83 | 35,09 | 32,75 | 30,70 | 28,91 | 27, ЗС | |
| 261,5 | 167,0 | 124,8 | 100,3 | 84,06 | 72,53 | 63,88 | 57,09 | 51,66 | 47,19 | 43,44 | 40,27 | 37,53 | 35,13 | 33,03 | 31,15 | |
| 321,4 | 197,6 | 145,3 | 115,8 | 96,50 | 82,94 | 72,78 | 64,91 | 58,63 | 53,44 | 49,13 | 45,47 | 42,34 | 39,61 | 37,22 | 35,09 |
Таблица 11 Значения r*=r/ctgq в зависимости от Т =QT/(mnl2) и q — 2пql/Q
Т при различных значениях q
| r* | 0.1 1 0,2 1 0,3 | 0,4 | 0,5 1 0,6 1 0,7 | 0,8 | 0,9 | 1,0 1 1,1 | 1.2 | 1,3 | 1.4 | 1,5 | |||||
| 0,091 | 5,56 | 2,44 | 1,62 | 1,25 | 1,03 | 0,88 | 0,81 | 0,75 | 0,62 | 0,62 | 0,62 | 0,50 | 0,50 | 0,50 | 0,50 |
| 0,182 | 16,28 | 6,09 | 3,81 | 2,81 | 2,31 | 2,000 | 1,75 | 1,62 | 1,50 | 1,38 | 1,25 | 1,25 | 1,25 | 1,00 | 1,00 |
| 0,273 | 34,44 | 11,44 | 6,69 | 4,81 | 3,88 | 3,25 | 2,88 | 2,62 | 2,38 | 2,25 | 2,12 | 2,00 | 2,00 | 2,00 | 1,50 |
| 0,364 | 62,25 | 19,16 | 10,63 | 7,41 | 5,78 | 4,19 | 3,75 | 3,50 | 3,25 | 3,00 | 3,00 | 2,75 | 2,50 | 2,50 | 2,00 |
| 0,454 | 103,0 | 30,06 | 16,00 | 10,78 | 8,25 | 6,75 | 5,81 | 5,19 | 4,75 | 4,38 | 4,12 | 4,00 | 3,75 | 3,50 | 3,00 |
| 0,545 | 161,3 | 45,34 | 23,28 | 15,28 | 11,44 | 9,25 | 7,88 | 6,94 | 6,31 | 5,88 | 5,50 | 5,25 | 5,00 | 5,00 | 4,50 |
| 0,636 | 245.4 | 67,09 | 33,50 | 21,43 | 15,69 | 12,50 | 10,50 | 9,19 | 8,25 | 7,62 | 7,12 | 6,75 | 6,50 | 6,25 | 5,50 |
| 0,727 | 370,1 | 99,06 | 48,31 | 30,25 | 21,69 | 17,00 | 14,12 | 12,19 | 10,87 | 9,94 | 9,25 | 8,75 | 8,50 | 8,00 | 7,50 |
| 0,818 | 569,1 | 149,8 | 71,56 | 43,87 | 30,94 | 23,81 | 19,44 | 16,63 | 14,69 | 13,31 | 12,38 | 11,63 | 11,00 | 10,75 | 10,00 |
| 0,909 | 949,1 | 246,3 | 115,5 | 69,44 | 48,00 | 36,25 | 29,19 | 24,56 | 21,44 | 19,25 | 17,63 | 16,50 | 15,75 | 15,25 | 14,50 |
|
|
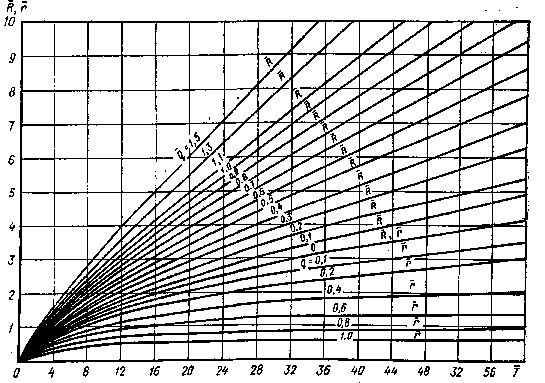
Рис. 17. График для определения Лиг при действии линейного водозабора в изолированном неограниченном водоносном горизонте: 
При отсутствии бытового потока (д = 0) соотношения (37) и (38) упрощаются и принимают следующий вид:
при R<1
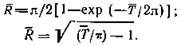(39) (40)
при R>10
Величины расстояний г до нижней границы ЗСО линейного водозабора, также найденные путем решения уравнения (36) по методу «предиктор — корректор» с использованием ЭВМ, даны в табл. 11 и на графике (см. рис. 17).
Приближенно величина r=r/l может быть оценена по следующим расчетным зависимостям:
при r<1
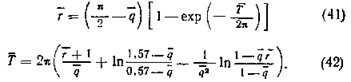
или при r> 1.
Очевидно, что максимальная протяженность rmax ЗСО линейного водозабора в направлении вниз по потоку подземных вод равна хр. При q=Q r=R.
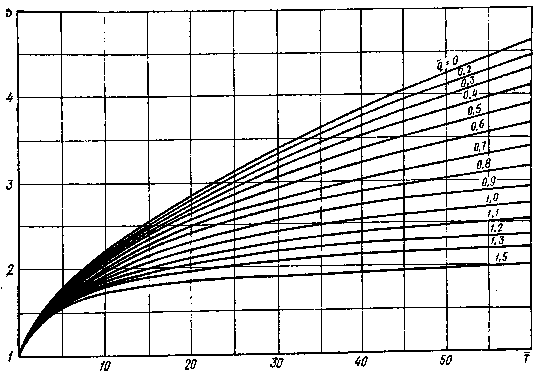
Рис. 18. График для определения ширины ЗСО линейного водозабора в изолированном неограниченном водоносном горизонте: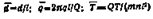 
На рис. 18 приведен график изменения максимальной ширины области захвата и, следовательно, ширины ЗСО линейного водозабора, ориентированного нормально к направлению потока подземных вод. График построен по результатам решения на ЭВМ системы уравнений, описывающих траекторию движения частиц воды. Численное решение системы также осуществлялось по методу «предиктор — корректор».
При относительно малых промежутках времени (T<20 — 30) для практических расчетов ширины ЗСО линейного водозаборного сооружения можно использовать простое балансовое соотношение
d=2QT/(nmnL). (43)
При расчетах на большие интервалы времени (R>10) ширину ЗСО водозаборов в виде прямолинейных рядов скважин можно оценивать так же, как при рассмотрении сосредоточенных водозаборных сооружений.
|
|
В предельном случае (Т->oo)
d=dmax=Q/2q. (44)
Пример расчета. Пусть проектный дебит линейного ряда скважин Q = е=10,5 тыс. м3/сут, длина водозаборного ряда 2100 м (l=1050 м), мощность водоносного горизонта т=25 м, коэффициент фильтрации k=80 м/сут, удельный расход бытового потока q — l м2/сут, пористость водоносных пород п =0,2.
Требуется выделить около проектируемого линейного водозабора третий пояс ЗСО, рассчитанный на 25 лет (Т~104 сут).
Протяженность ЗСО водозабора вверх и вниз по потоку получаем по графику приведенному на рис. 17. Значения безразмерных параметров, определяющих величины R и r, равны: Т= (10 500*104)/(0,2*25*10502)=19; q= (2*3.14*1050)710500=0,6 и, следовательно, Я = 3,6, г=1,2, откуда R=Rl =3,6-1050=3700 м, r=rl= 1,2*1050=1260 м, L = R+r= 3700+1260=4960 м.
Ширину ЗСО находим по графику на рис. 18. При Г=19 и #=0,6 3=2,5. Следовательно, d=2,5*1050=2600 м. По приближенному соотношению (43)
d=(2*1050*104)/(3,14*25*0,2*4960)=270 м.