Изолированные водоносные горизонты характеризуются отсутствием внешних источников питания подземных вод (инфильтрация, перетекание из соседних водоносных пластов и т. д.). Водозабором извлекается вода из естественного грунтового потока, т. е.
Q=Qe. (14)
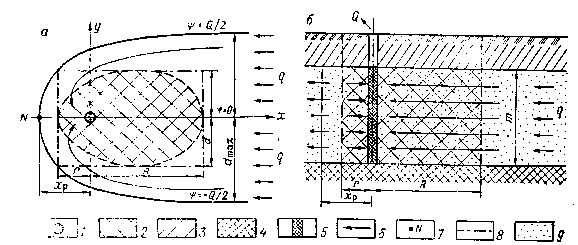
Рис. 14. Схема к расчету ЗСО сосредоточенного водозабора в изолированном водоносном горизонте в удалении от поверхностных водотоков:
а — план; б — разрез; 1 — водозабор; 2 — область захвата; 3 — суглинок- 4 — водоупор- 5 — фильтр скважины; 6 — направление естественного потока подземных вод- 7 — раздельная точка; 8 — граница ЗСО; 9 — водоносный горизонт
Таблица 7
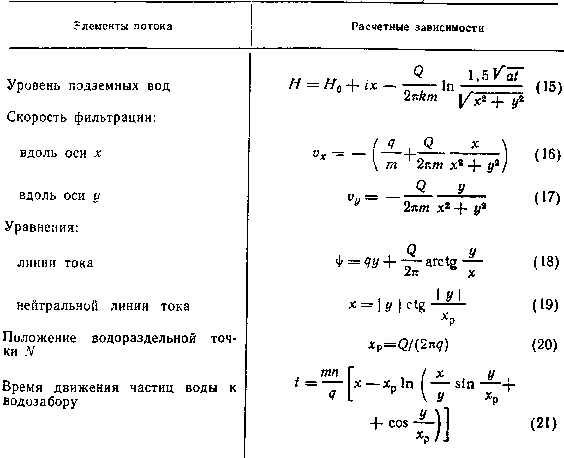
Примечания: H0 — уровень в створе х=0; i — уклон естественного потока; Q — Дебит водозабора; k — коэффициент фильтрации; т — мощность; а — коэффициент пьезо-проводности; q — удельный расход естественного потока; Ф — значение функции тока — — Q/2<Ф<Q/2; t — время; п — пористость.
Характерным для рассматриваемых водораздельных водозаборов является также неустановившийся режим фильтрации подземных вод в течение всего срока эксплуатации водозаборов. В связи с этим не только область захвата, но и область питания водозаборного сооружения в изолированных горизонтах непрерывно расширяется, охватывая все большие площади. Для расчета положения ЗСО водозаборов подземных вод целесообразно исходить из условий квазиустановившейся фильтрации в пределах всей области захвата водозабора. При этом, как показывают расчеты, весьма незначительно увеличиваются скорости движения подземных вод и несколько завышаются размеры ЗСО. Использование указанной предпосылки дает возможность вместо рассмотрения траектории движения частиц воды при определении границ ЗСО использовать также линии тока подземных вод, что значительно упрощает расчеты.
Схема неограниченного водоносного горизонта соответствует условиям эксплуатации водозаборного сооружения в достаточно протяженном по площади водоносном горизонте, когда естественные границы горизонта (реки, водоемы, участки выклинивания пород) находятся за пределами области влияния водозабора.
Сосредоточенный водозабор. Расчетные зависимости (15) — (21) для определения основных элементов фильтрационного потока при работе одиночного или группового сосредоточенного водозабора в неограниченном изолированном горизонте при наличии естественного потока подземных вод с интенсивностью q (рис. 14) приведены в табл. 7. Используя эти формулы и данные Приложения, можно определить основные параметры ЗСО водозаборов в рассматриваемых гидрогеологических условиях.
Используя выражение (16), при y=0 и x>0 по формуле (13) можно получить уравнение для определения протяженности ЗСО вверх по потоку подземных вод [13]:
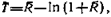 (22)
(22)
где T=qT/(mnxp); R=R/x9.
Подставляя в формулу (13) выражение (16) при y — Q и x<0, получим выражение для определения протяженности ЗСО вниз по потоку подземных вод от водозабора:
T= — [ln(l — r)+r]; (23)
где r =r/хp. Очевидно, что максимально возможное значение параметра г равно 1, т. е.
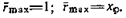 (24)
(24)
Ширина ЗСО в данном случае может быть найдена следующим образом. Сначала определим абсциссу и ординату точки, находящейся на границе зоны захвата и максимально удаленной от оси х(х — х*; y=d). Для этого используем то обстоятельство, что время движения этой точки до водозабора минимально в сравнении с соответствующим временем движения других точек с линии y=d до водозабора. Следовательно, должно выполняться условие
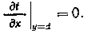 (25)
(25)
Подставляя в выражение (25) уравнение (21), получим
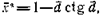 (26)
(26)
где х*=х*/хр; d=d/xp.
После подстановки (26) в (21) найдем соотношение, связывающее ширину SCO d с расчетным временем Т:
T=l — dctgd — ln(smd/d). (27)
Из уравнения (27) видно, что максимальное значение параметра d, теоретически достигаемое при бесконечном расчетном времени 7, равно я, т. е.
dmах = п; d= п xp = Q/2q. (28)
Графики изменения функций R, г, и d в зависимости от величины Т, определенные по формулам (22), (23) и (27), показаны на рис. 15; в табл. 8 приведены численные значения параметров ЗСО. При T<20 — 30 для оценки величины d с погрешностью не более 10% может быть использовано приближенное балансовое соотношение
d=2TQ/(nmnL), (28a)
где L=R+r.
При q=0, т. е. при отсутствии бытового потока подземных вод xр->оо и из соотношений (22), (23) и (27) следует, что
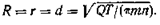 (29)
(29)
Пример расчета. Водозабор представлен одной эксплуатационной скважиной производительностью Q = 2 тыс. м3/сут. Намечаемый к использованию водоносный горизонт имеет среднюю мощность m=40 м, коэффициент фильтрации k=50 м/сут, водопроводимость km = 40*50 = 2 тыс. м2/сут, активную пористость n= 0,2. Уклон естественного потока в районе проектируемой скважины i=0,001 (q=kmi = 2 м2/сут).
Требуется определить границы третьего пояса ЗСО водозабора (T=10* сут). Установим сначала положение водораздельной точки N. По формуле (20) получим Хр = 2000/(2*3,14*2) = 160 м. Исходный параметр т, полученный по формуле (22), в данном случае будет равен T=2*104/(40*0,2*160) = 15,6. Следовательно (см. табл. 8), R=18,6; r=1; 3=2,9. Переходя к размерным величинам R, r и d, получим R= 18,6*160~2980 м; r= 1*160= 160 м; d=2,9*160=470 м.
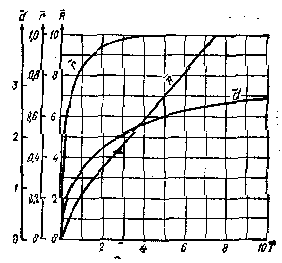
Рис. 15. График для определения R, r, d при действии сосредоточенного водозабора в изолированном неограниченном водоносном горизонте: R = R/xр; r = r/xp; d=d/xp; xp = Q/(2 п q); T= qT/(mnXp)
Линейный водозабор. Такие сооружения чаще всего располагаются нормально к направлению естественного потока подземных вод. Схема фильтрации к водозабору для этого случая представлена на рис. 16. В табл. 9 даются [3, 11, 12, 16, 25] соотношения, характеризующие гидродинамические показатели фильтрационного потока к линейному водозабору: распределение напоров, скорости течения подземных вод, потенциальная функция, функция тока и т. д.
Таблица 8
Величины R, r и d в зависимости от расчетного времени т к формулам (22), (23) и (27)
| т | R | r | d | Т | R | г | d |
| 0,01 | 0,149 | 0,135 | 0,142 | 7,091 | 0,998 | 2,415 | |
| 0,02 | 0,213 | 0,187 | 0,200 | 8,222 | 0,999 | 2,522 | |
| 0,05 | 0,351 | 0,284 | 0,315 | 9,336 | 2,605 | ||
| 0,1 | 0,517 | 0,384 | 0,445 | 10,437 | 2,670 | ||
| 0,2 | 0,773 | 0,507 | 0,626 | 11,528 | 2,722 | ||
| 0,3 | 0,987 | 0,589 | 0,762 | 12,611 | 2,765 | ||
| 0,5 | 1,358 | 0,699 | 0,973 | 17,942 | 2,895 | ||
| 2,147 | 0,842 | 1,338 | 23,186 | 2,961 | |||
| 3,506 | 0,948 | 1,789 | 33,543 | 3,025 | |||
| 4,750 | 0,982 | 2,074 | 54,008 | 3,074 | |||
| 5,937 | 0,994 | 2,271 | 104,661 | 3,109 |
Конфигурация области питания линейного водозабора, работающего в неограниченном изолированном пласте, аналогична области питания сосредоточенного водозаборного сооружения. Раздельная линия, ограничивающая область питания водозабора, в данном случае также имеет водораздельную точку N. Ее положение определяется соотношением (35). Очевидно, что в питании водозабора участвуют только подземные воды естественного потока, которые полностью определяют качество воды, извлекаемой водозабором.
Протяженность ЗСО линейного водозабора вверх R и вниз r по потоку подземных вод, а также ширину ЗСО удобно рассчитывать по формуле (36), характеризующей движение отдельных частиц воды при работе водозаборного сооружения. Для решения уравнения (36) применен метод «предиктор — корректор» с использованием ЭВМ.
Величину R можно найти с помощью табл. 10 и графика (рис. 17). В некоторых случаях можно использовать приближенные зависимости, полученные путем интегрирования выражения (36) с учетом приближенных соотношений arcctgx=n/2 — x при x<1 и arcctgx~1 /x при x>1. Эти зависимости имеют вид:
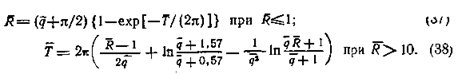
Формула (37) применима при расчетах на относительно малые промежутки времени в основном для обоснования размеров второго пояса ЗСО, а выражение (38) используется для расчетов третьего пояса на большие интервалы времени.
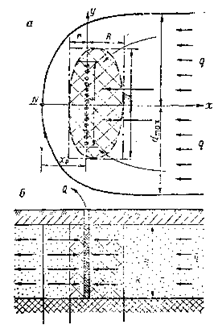
Рис. 16. Схема фильтрации к линейному водозабору в неограниченном пласте: а — план; б — разрез. Условные обозначения см. на рис. 14
Та бл и ц а 9