Балансовый метод – изучает балансовые связи и заключается в построении балансовых таблиц (характеризует структуру совокупности, позволяет определить искомые показатели из балансовой зависимости, группировать единицы совокупности по различным признакам и т.д.).
Индексный метод – изучает компонентные связи с помощью построения систем взаимосвязанных индексов.
Метод группировок – изучает факторные связи (заключается в разделении всей совокупности на группы по факторному признаку; позволяет выявить наличие связи и ее направление).
Корреляционно-регрессионный метод – изучает факторные (корреляционные) связи.
Регрессионный анализ заключается в определении аналитического выражения связи, т.е. подборе такой формы функциональной связи, которая в наибольшей степени соответствует сущности обнаруженной корреляционной зависимости.
Корреляционный анализ позволяет определить тесноту связи, т.е. с помощью специальных показателей измерить, в какой мере корреляционная связь приближается по своей силе к связи функциональной.
Корреляционно-регрессионный анализ проводится в несколько этапов:
1. Выбор типа функции
2. Построение уравнения регрессии
3. Оценка значимости параметров регрессии
4. Измерение тесноты связи
27. Основные методы изучения взаимосвязей.
Важное место в статистическом изучении взаимосвязей занимают следующие методы:
1. Метод приведения параллельных данных.
2. Метод аналитических группировок.
3. Графический метод.
4. Балансовый метод.
5. Индексный метод.
6. Корреляционно-регрессионный.
1. Сущность метода приведения параллельных данных заключается в следующем:
Исходные данные по признаку X располагаются в порядке возрастания или убывания, а по признаку Y записываются соответствующие им показатели. Путем сопоставления значений X и Y, делается вывод о наличии и направлении зависимости.
3. Сущность графического метода составляет наглядное представление наличия и направления взаимосвязей между признаками. Для этого значение факторного признака X располагается по оси абсцисс, а значение результативного признака по оси ординат. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости. При этом возможны следующие варианты:
а \, б/ (вверх), в\ (вниз).
Если точки на графике расположены беспорядочно (а), то зависимость между изучаемыми признаками отсутствует.
Если точки на графике концентрируются вокруг прямой (б)/, зависимость между признаками прямая.
Если точки концентрируются вокруг прямой (в)\, то это свидетельствует о наличии обратной зависимости.
На основе метода параллельных данных и графического метода, могут быть рассчитаны показатели, характеризующие степень тесноты корреляционной зависимости.
Наиболее кратным из них является коэффициент знаков Фехнера. Он рассчитывается по формуле:
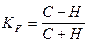
C - сумма совпадающих знаков отклонений индивидуальных значений признака от средней.
H - сумма несовпадений
Данный коэффициент изменяется в пределах (-1;1).
Значение KF=0 свидетельствует об отсутствии зависимости между изучаемыми признаками.
Если KF=±1, то это говорит о наличии функциональной прямой (+) и обратной (-) зависимости. При значении KF>½0,6½ делается вывод о наличии сильной прямой (обратной) зависимости между признаками. Кроме того на основе исходных данных о факторном и результативном признаках, может быть рассчитан коэффициент корреляции рангов Спирмена, который определяется по формуле:

 - квадраты разности рангов
- квадраты разности рангов
(R2-R1), n - число пар рангов
Данный коэффициент, как и предыдущий, изменяется в тех же пределах и имеет одинаковую с KF экономическую интерпретацию.
В тех случаях, когда значение X или Y выражаются одинаковыми показателями, коэффициент корреляции рангов рассчитывается по следующей формуле:

tj - одинаковое число рангов в j - ряду
Если исследуется зависимость между тремя и более математическими признаками, то для ее исследования применяется коэффициент конкордации определяемый по формуле:

m - количество факторов
n - число наблюдений
S - отклонение суммы квадратов рангов от средней квадратов рангов