1. Сопоставимость по территории – предполагает одни и те же границы территории. Так, при характеристике повышения экономической мощи страны следует использовать данные в имеющихся границах территории, а при изучении темпов экономического развития следует брать данные по территории в одних и тех же границах.
2. Сопоставимость по кругу охватываемых объектов – сопоставляемые показатели должны быть однородны. Например, при характеристике динамики численности студентов ВУЗов по группам нельзя в одни годы учитывать только численность студентов дневного обучения, а в другие - численность студентов всех видов обучения.
3. Сопоставимость по времени регистрации – обеспечивается равенством периодов времени, за который приводятся данные.
4. Сопоставимость по ценам – при приведении к сопоставимому виду продукции, измеренной в стоимостных показателях трудность заключается в том, что с течением времени происходит непрерывное изменение цен, а во вторых несколько видов цен. Для характеристики изменения объема продукции должно быть устранено влияние изменения цен. Поэтому на практике продукцию, произведенную в различные периоды оценивают в ценах одного и того же базисного периода, которые называют сопоставимыми.
Смыкание рядов динамики - объединение в одни ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам.
Условия смыкания рядов; необходимо, чтобы по одному из периодов (переходному) имелись данные, исчисленные по разной методологии (или в разных границах).
23. Аналитические показатели ряда динамики.
При описании рядов динамики используют показатели, характеризующие интенсивность их изменения во времени и систему средних показателей.
Анализ интенсивности изменения во времени осуществляется с помощью следующих аналитических показателей.
1. Абсолютный прирост. Показывает, на сколько каждый из уровней ряда отличается от уровня, принятого за базу (разность между уровнями ряда).
Введем обозначения:
 – начальный уровень (первый, базисный);
– начальный уровень (первый, базисный);
 – какой-либо уровень;
– какой-либо уровень;
 – последний уровень.
– последний уровень.
Абсолютный прирост вычисляется по следующим формулам:
 – базисный абсолютный прирост;
– базисный абсолютный прирост;
 – цепной абсолютный прирост.
– цепной абсолютный прирост.
Взаимосвязь: сумма всех последовательных цепных абсолютных приростов равна базисному абсолютному приросту за исследуемый период (последнему базисному):
 .
.
2. Темп роста (коэффициент роста) – отношение каждого уровня ряда к уровню, принятому за базу сравнения. Показывает, во сколько раз каждый уровень ряда больше уровня, принятого за базу, или сколько процентов от него составляет.
 – базисный темп роста;
– базисный темп роста;
 – цепной темп роста.
– цепной темп роста.
Выражается в процентах или в виде коэффициента.
3. Темп прироста – отношение абсолютного прироста к уровню ряда, принятому в качестве базы сравнения. Показывает, на сколько процентов изменяется каждый уровень ряда по сравнению с уровнем, принятым за базу.
 – базисный темп прироста;
– базисный темп прироста;
 – цепной темп прироста.
– цепной темп прироста.
Он может быть вычислен и по такой формуле:
 ,
,
которая получается из первых двух следующим образом:
 .
.
Для цепного темпа прироста рассуждения аналогичные.
4. Абсолютное значение одного процента прироста. Показывает отношение абсолютного прироста к темпу прироста:
 .
.
Абсолютное значение одного процента прироста может быть вычислено и по такой формуле:
 ,
,
которая выводится путем несложных преобразований из первой.
24. Средние показатели в рядах динамики.
Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.
Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).
В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е.
 =
= 
Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как 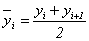 . Количество таких средних будет
. Количество таких средних будет 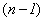 . Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать
. Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать
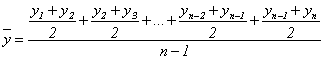 .
.
После преобразования числителя получаем
 ,
,
где Y1 и Yn — первый и последний уровни ряда; Yi — промежуточные уровни.
Эта средняя 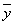 известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.
известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.
В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е.
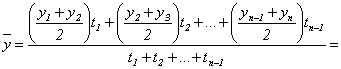
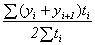 .
.
В данном случае предполагается, что в промежутках между датами уровни принимали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi остается неизменным до следующего (i+ 1 )- го момента, т.е. известна точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:
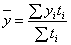 ,
,
где  – время, в течение которого уровень
– время, в течение которого уровень  оставался неизменным.
оставался неизменным.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть
 Б =
Б = 
Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть
 Ц =
Ц = 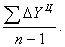
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.
Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными.
Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.
Базисное среднее относительное изменение определяется по формуле
 Б=
Б=  =
= 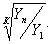
Цепное среднее относительное изменение определяется по формуле
 Ц=
Ц= 
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.
25. Методы изучения сезонных явлений. Коэффициент сезонности. Графическое изображение рядов динамики.
К сезонным относят явления, в которых отчетливо выражены внутригодовые изменения уровней ряда, т.е. более или менее устойчиво повторяющиеся из года в год колебания уровней. Эти колебания чаще всего связаны со сменой времен года. К сезонным явлениям относят, например, потребление электроэнергии; неравномерность производственной деятельности в отраслях пищевой промышленности, связанных с переработкой сельскохозяйственного сырья; перевозки пассажирским транспортом; спрос на многие виды продукции и услуг и т.д.
Для измерения сезонных колебаний статистикой предложены следующие методы:
•метод абсолютных разностей;
• • метод относительных разностей;
• • построение индексов сезонности.
Первые два способа предполагают нахождение разностей фактических уровней и теоретических уровней (найденных при выявлении основной тенденции развития, либо методом средних величин).
Способ абсолютных разностей: Yi - Yтеор
Метод относительных разностей определяют отношение абсолютных размеров указанных разностей к теоретическому уровню (Yi - Yтеор)/Yтеор.
При выявлении основной тенденции используют метод скользящей средней, аналитическое выравнивание, либо методом средних величин.
Для измерения сезонных колебаний необходимы данные не менее чем за трехлетний период, для того чтобы устранить случайные колебания.
| Методы измерения сезонных волн, основанные на применении | Наименование методов вычисления сезонных волн |
| I. Средней арифметической | 1. Метод абсолютных разностей 2. Метод отношений средних помесячных к средней за весь период 3. Метод отношений помесячных уровней к средней данного года |
| II. Относительных величин | 1. Метод относительных величин 2. Метод относительных величин на основе медианы 3. Метод У. Персона (цепной метод) |
| III. Механического выравнивания | 1. Метод скользящих средних 2. Метод скользящих сумм и скользящих средних |
| IV. Аналитического выравнивания | 1. Выравнивание по прямой 2. Выравнивание по параболе и экспоненте 3. Выравнивание по ряду Фурье |
Динамика явлений графически может быть представлена в виде линейной диаграммы. Для построения которой используется система прямоугольных координат - по оси абсцисс откладывается время, а по оси ординат - либо уровни, либо базисные темпы роста.
Можно указать на следующие важные моменты в построении линейных графиков:
1) на графике должен строго соблюдаться масштаб уровня и масштаб времени;
2) каждая точка оси абсцисс выражает момент времени, а отрезки шкалы - периоды времени;
3) периоды (годы, месяцы и т.п.) в принципе должны подписываться под отрезком шкалы, уровни интервального ряда могут быть выражены, строго говоря, только столбиками, а потому точка на графике обозначает высоту столбика;
4) моменты времени подписывают под точками шкалы, вершины ординат (обозначение точками) соответствуют уровням этих моментов;
5) точки соединяют отрезками прямых, которые образуют ломаную кривую, характеризующую процесс динамики. Соединять точки отрезками кривых линий (“закругленных”) недопустимо.
26. Понятие, виды и задачи взаимосвязей общественных явлений.
Общественное явление, таким образом, есть взаимосвязанное действие поведения индивидов, вызывающее определенные изменения в природе, обществе, а также в поведении этих индивидов и в них самих. Как и любое явление, оно есть часть реального мира, но при этом имеет и определенные специфические черты, которые обнаруживают себя как в его сущности, так и в формах, которые он принимает.