1. Выбор группировочного признака
В зависимости от вида группировочных признаков различают группировки по количественным и качественным (атрибутивным) признакам.
2. Определение числа групп:
Если в основании группировки атрибутивный (качественный) признак, то количество групп равняется количеству значений этого признака
3. Выбор интервала группировки:
Интервал группировки — это значение варьирующего признака, лежащее в определенных пределах. Нижняя граница интервала — это значение наименьшего признака в интервале. Верхняя граница — это наибольшее значение в интервале.
Величина интервала — это разница между верхней и нижней границами.
Интервалы группировок могут быть равными и неравными.
Равные интервалы применяются в тех случаях, когда значение количественного признака внутри совокупности изменяется равномерно.
Величина равных интервалов определяется по формуле:

§  — величина интервала
— величина интервала
§ 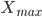 - максимальное значение признака в совокупности
- максимальное значение признака в совокупности
§  — минимальное значение признака в совокупности
— минимальное значение признака в совокупности
§ 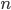 — число групп
— число групп
Для того чтобы найти скопление (в мерном пространстве) объектов (точек), необходимо применить многомерную группировку. Различают группировки по используемой информации:
1) первичные – производятся на основе исходных данных которые были получены в результате статистического наблюдения;
2) вторичные – это результат соединения или расчленения группировки.
9. Статистическая таблица и ее элементы. Принципы построения и виды статистических таблиц.
Статистической называется таблица, которая содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа.
Статистическая таблица - это цифровое выражение итоговой характеристики всей наблюдаемой совокупности или её составных частей по одному или нескольким существенным признакам.
Основные элементы статистической таблицы, составляющие как бы её остов (основу), показаны на рис.
Название таблицы (общий заголовок)
| Содержание строк | Наименование граф (верхние заголовки) | |||||
| А | … | |||||
| Наименование срок (боковые заголовки) | ||||||
| Итоговая строка | Итоговая графа |
Статистическая таблица содержит три вида заголовков: общий, верхние и боковые.
Общий заголовок отражает содержание всей таблицы (к какому месту и времени она относится), располагается над макетом таблицы по центру и является внешним заголовком.
Верхние заголовки характеризуют содержание граф (заголовки сказуемого), а боковые (заголовки подлежащего) – строк. Они являются внутренними заголовками.
В зависимости от построения подлежащего статистические таблицы подразделяются на три вида: простые, групповые, и комбинированные.
Простыми называются такие статистические таблицы, в подлежащих которых имеется только перечень показателей, раскрывающих содержание подлежащего.
Макет простой таблицы
| Перечень объектов | Значения показателей |
Групповыми называются такие статистические таблицы, в которых изучаемый объект разделен в подлежащем на группы по тому или иному признаку.
Групповые таблицы, как правило, возникают в результате применения метода группировок.
Макет групповой таблицы
| Наименование группы | Количество объектов в группе | |
| единиц | % | |
Комбинационной таблицей называется такая таблица, в которой в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации: изучаемый объект разбит на группы, а внутри групп на подгруппы. Макет комбинационной таблицы
| Наименование объекта | Признаки или границы интервалов по признаку | |||
Основные правила построения статистических таблиц:
1) в заголовке должны быть отражены объект, признак, время и место совершения события;
2) графы и строки следует нумеровать;
3) графы и строки должны содержать единицы измерения;
4) сопоставляемую в ходе анализа информацию располагают в соседних графах (либо одну под другой);
5) числа в таблице проставляют в середине граф, строго одно под другим; числа целесообразно округлять с одинаковой степенью точности;
6) отсутствие данных обозначается знаком умножения*, если данная позиция не подлежит заполнению, отсутствие сведений обозначается многоточием (...), либо н.д., либо н. св., при отсутствии явления ставится знак тире (-);
7) для отображения очень малых чисел используют обозначение 0.0 или 0.00; если число получено на основании условных расчетов, то его берут в скобки, сомнительные числа сопровождают вопросительным знаком, а предварительные – знаком.
10. Статистические графики, их виды и правила построения.
Статистический график - условное изображение, посредством которого статистической совокупности, характеризуемые определенными показателями, отображаются в виде различных геометрических образов-линий, точек, плоскостных или объемных фигур, а также разнообразных символов.
1. По способу построения статистические графики делятся на диаграммы и статистические_карты.
Диаграммы – наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном) независимых друг от друга величин: территорий, населения и т.д.
Статистические карты – графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том, что представляют собой условные изображения статистических данных на контурной географической карте, т.е. показывают пространственное размещение или пространственную распространенность статистических данных.
Геометрические знаки – точки, либо линии или плоскости, либо геометрические фигуры, поэтому различают графики точечные, линейные, плоскостные и пространственные (объемные).
При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных – линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и подразделяются на столбиковые, полосовые, круговые, квадратные и фигурные.
Статистические карты по графическому образу делятся на картограммы и картодиаграммы.
2. В зависимости от круга решаемых задач выделяют диаграммы сравнения, структурные диаграммы и диаграммы динамики. Особым видом графиков являются диаграммы распределения величин, представленных вариационным рядом. Это гистограмма, полигон, и др.
3. по форме геометрического образа:
v линейные графики (кривые);
v плоскостные графики (столбики, полосы);
v объемные графики (в виде поверхностных распределений).
Существуют следующие виды статистических графиков:
1) ряды распределения;
2) структура статистической совокупности;
3) ряды динамики;
4) показатели связи;
5) показатели выполнения заданий.
Правила построения стат графиков: Необходимо правильно подобрать поле графика. На графике должны быть изображены масштабные ориентиры, шкалы, указаны ед. измерения, линии фигуры, подписи к ним должны выполняться с соблюдением обычных правил «построения и оформления чертежей. Графики подписываются снизу(н\р:Рис.2). Подпись графика должна отображать всё содержание материалов, отображенного на графике.
11. Абсолютные статистические показатели.
Абсолютные статистические показатели всегда являются именованными числами. В зависимости от социально-экономической сущности исследуемых явлений, их физических свойств они выражаются в натуральных, стоимостных или трудовых единицах измерения.
· Натуральные единицы измерения отражают естественные свойства явлений и измеряются в физических единицах меры веса, объема, протяженности и т.д. В международной практике используются такие натуральные единицы измерения как тонны, килограммы, квадратные, кубические и простые метры, мили, километры, галлоны, литры, штуки и т.д.
· Стоимостные единицы измерения отражают несоизмеримые в натуральном выражении процессы и представляют собой их денежное выражение. Денежная оценка социально-экономических явлений и процессов приобретает наибольшее значение в условиях рыночной экономики.
· К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.
· Виды абсолютных величин:
· · Индивидуальные – отражают размеры количественных признаков у отдельных единиц изучаемой совокупности.
· · Общие – выражают размеры, величину количественных признаков у всей изучаемой совокупности в целом.
· Абсолютные величины отражают наличие тех или иных ресурсов, это основа материального учета. Они наиболее объективно отражают развитие экономики.
· Различают количественные и качественные абсолютные показатели.
· Количественные показатели определяются путем подведения итогов по совокупности или ее части. К количественным показателям относится физический объем выпуска продукции – q, численность персонала - Т, выработка продукции в единицу времени – w.
· Качественные показатели представляют характеристику совокупности, но имеют размерность обобщающего признака. Р - цена.
12. Относительные статистические показатели.
Относительный показатель представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений. Относительный показатель, полученный в результате соотнесения разноименных абсолютных показателей, в большинстве случаев должен быть именованным. (например, производство какой-либо продукции в соответствующих единицах измерения в расчете на душу населения). Все используемые на практике относительные статистические показатели можно подразделить на следующие виды: 1) динамики; 2) плана; 3) реализации плана; 4) структуры; 5) координации; 6) интенсивности и уровня экономического развития; 7) сравнения.
Относительный показатель динамики (ОПД) = Текущий показатель / Предшествующий или базисный показатель, показывает, во сколько раз текущий уровень превышает предшествующий (базисный) или какую долю от последнего составляет.
Относительный показатель координации ОПК = Показ., характериз. i-ю часть совокупн. / Показ., характериз. часть совокупн., выбранную в качестве базы сравнения. Относительный показатель интенсивности характеризует степень распространения изучаемого процесса: ОПИ = Показатель, характеризующий явление А / Показатель, характеризующий среду распространения явления А. Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Относительный показатель сравнения представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):ОПСр = Показатель, характеризующий объект А / Показатель, характеризующий объект В. Для выражения данного показателя могут использоваться как коэффициенты, так и проценты.
13. Средние статистические показатели. Степенные средние величины.
Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
Величина средней дает обобщающую количественную характеристику всей совокупности и характеризует ее в отношении данного признака.
Сущность средней заключается в том, что в ней взаимопогашаются случайные отклонения значений признака и учитываются изменения вызванные основным фактором.
Важнейшими условиями (принципами) для правильного вычисления и использования средних величин является следующие:
1. В каждом конкретном случае необходимо исходить из качественного содержания осредняемого признака, учитывать взаимосвязь изучаемых признаков и имеющиеся для расчета данные.
2. Индивидуальные значения, из которых вычисляются средние, должны относиться к однородной совокупности, а число их должно быть значительным.
Степенные средние:
§ Арифметическая
§ Гармоническая
§ Геометрическая
§ Квадратическая
§ Степенные средние величины исчисляются в двух формах — простой и взвешенной.
§ Простая средняя величина считается по несгруппированным данным и имеет следующие общий вид:
§  ,
,
§ где X i – варианта (значение) осредняемого признака;
§ m – показатель степени средней;
§ n – число вариант (наблюдений).
§ Взвешенная средняя величина считается по сгруппированным данным, представленным в виде дискретных или интервальных рядов распределения:  , где X i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
, где X i – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
§ m – показатель степени средней;
§ fi – частота, показывающая, сколько раз встречается i -e значение осредняемого признака.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:
 .
.
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:  .
.
Средняя гармоническая величина, как и средняя арифметическая может быть простой и взвешенной. Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую:
 .
.
Однако в статистической практике чаще применяется средняя гармоническая взвешенная:
 , где m = xf,
, где m = xf,
она используется, как правило, при расчете общей средней из средних групповых.
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Ее формула такова:
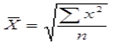 , для простой.
, для простой.
 , для взвешенной.
, для взвешенной.
Формула средней квадратической используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения. Так, при расчете показателей вариации среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины.
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину.
Ее формула такова:
 , для простой.
, для простой.
 , для взвешенной.
, для взвешенной.
Наиболее часто формулу средней геометрической используют для определения средних валютных курсов, эффективности валютных курсов,
реальной эффективности валютных курсов (международная финансовая статистика).
14. Структурные средние.
Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.
Мода (Мо) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.
Мода представляет наиболее часто встречающееся или типичное значение.
Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен.
В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность).
Формула моды для интервальных вариационных рядов с равными интервалами:

 – нижняя граница модального интервала (интервала,
– нижняя граница модального интервала (интервала,
 – частота модального интервала
– частота модального интервала
 – частота предмодального интервала
– частота предмодального интервала
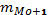 – частота постмодального интервала
– частота постмодального интервала
 – ширина модального интервала.
– ширина модального интервала.
Медиана (Ме – это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения.
Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.
Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.
Медиана в интервальных вариационных рядах рассчитывается по формуле:

где х 0 – нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот);
 – величина медианного интервала;
– величина медианного интервала;
 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
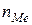 – частота медианного интервала.
– частота медианного интервала.
15. Понятие и основные показатели вариации.
Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Размах вариации представляет собой разность максимального и минимального значений признака: R = Xmax – Xmin. Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ.
Упрощенный способ расчета дисперсии осуществляется с помощью следующих формул (простой и взвешенной):
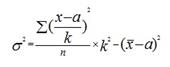
|

|
Широко распространенным на практике показателем является среднее квадратическое отклонение: 
|
Среднее квадратическое отклонение определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак.
Рассмотренные показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. В отличие от них, коэффициент вариации измеряет колеблемость в относительном выражении - относительно среднего уровня, что во многих случаях является предпочтительнее.

|
- формула для расчета коэффициента вариации.
16. Использование показателей вариации в анализе взаимосвязей.
Для выявления взаимосвязи исходная совокупность делится на две или более групп во факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:
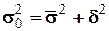 (6.8)
(6.8)
где 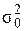 - общая дисперсия;
- общая дисперсия;
 - средняя из внутригрупповых дисперсий;
- средняя из внутригрупповых дисперсий;
 - межгрупповая дисперсия.
- межгрупповая дисперсия.
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней:
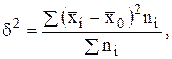 (6.9)
(6.9)
где 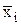 - среднее значение результативного признака по i-ой группе;
- среднее значение результативного признака по i-ой группе;
 - общая средняя по совокупности в целом;
- общая средняя по совокупности в целом;
 - объем (численность) i-ой группы.
- объем (численность) i-ой группы.
Если факторный признак, по которому производилась группировка, не оказывает никакого влияния не признак результативный, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равна нулю.
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:
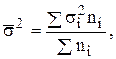 (6.10)
(6.10)
где  -дисперсия результативного признака в i-ой группе;
-дисперсия результативного признака в i-ой группе;
 -объем (численность) i-ой группы.
-объем (численность) i-ой группы.
Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:
 (6.11)
(6.11)
Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.
17. Понятие об индексах в статистике, классификация индексов.
Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве.
Статистика осуществляет классификацию индексов по следующим признакам:
1. В зависимости от объекта исследования:
§ индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)
§ индексы качественных показателей (индексы цен, себестоимости, заработной плата)
К индексам объемных показателей относятся индексы физического объема: товарооборота, продукции, потребления материальных благ и услуг; а также других показателей, имеющих количественный характер: численности работников, посевных площадей и т.п. К индексам качественных показателей относятся индексы: цен, себестоимости продукции, заработной платы, производительности труда, урожайности и т.п.;
2. По степени охвата элементов совокупности:
§ индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)
§ общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)
3. В зависимости от методологии исчисления общие индексы подразделяются на:
§ агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).
§ средние (являются производными от агрегатных)
4. В зависимости от базы сравнения различают:
§ базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)
§ цепные (если база сравнения постоянно меняется)
18. Индивидуальные и общие индексы.