Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности.
Если за основу группировки взят качественный признак, то такой ряд распределения называют 
атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).
Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).
Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений.
Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.
Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд.
19 Статистика национального богатства: основные понятия и категории. Состав и структура национального богатства.
национальное богатство представляет собой совокупную стоимость всех экономических активов материальных (природные ресурсы) и нематериальных (нефинансовых и финансовых активов) в рыночных ценах, находящихся в собственности резидентов данной страны на территории страны или за ее пределом, а также, за вычетом их финансовых обязательств, как резидентам, так и нерезидентам.
|
|
Составляющие национального богатства:
природные ресурсы (земля, полезные ископаемые, энергетические ресурсы, лес и животный мир), которые являются учтенными и вовлеченными в оборот. Как характерную особенность природных ресурсов можно выделить то, что они являются невоспроизводимыми благами.
• материальные ресурсы, приобретенные в результате накопленного труда. Материальные ресурсы можно производить в любое время, следовательно, они являются воспроизводимыми благами;
национальное имущество – складывается в процессе производства, в него входят:
• основные фонды (здания, сооружения, транспортные средства, машины, оборудование и т. д.). Статистические данные основных фондов характеризуют их общее состояние, перспективы развития основных фондов по всей стране и отдельно в каждой отрасли;
• оборотные фонды (производственные запасы – сырье, материалы, топливо, запчасти; незавершенное производство; готовая продукция, материальные резервы и т. д.);
• личное имущество. Статистические данные о национальном имуществе используется для оценки уровня экономического развития;
• накопленный научно-технический потенциал;
• интеллектуальный потенциал.
20. Расчет общих индексов и определение влияния факторов на стоимостные приросты продукции. Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega - присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных).
|
|
21. Виды средних величин и формулы их расчета. Значение структурных средних. Средней величиной называется статистический показатель, который дает обобщенную характеристику варьирующего признака однородных единиц совокупности.
Виды средних величин
Средние величины делятся на два больших класса: степенные средние и структурные средние
Степенные средние:
§ Арифметическая
§ Формула средней арифметической (простой) имеет вид
§ 
(5.2)
§ где n - численность совокупности.
§ Гармоническая
Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
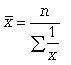
§ Геометрическая
§ Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.
|
|
§ Для простой средней геометрической
§ 
§ Квадратическая
§ Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).
§ Формула простой средней квадратической
§ 
(5
Структурные средние:
§ Мода
где:
§ 
— значение моды
§ 
— нижняя граница модального интервала
§ 
— величина интервала
§ 
— частота модального интервала
§ 
— частота интервала, предшествующего модальному
§ 
— частота интервала, следующего за модальным
§ Медиана
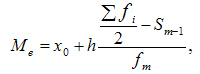
где:
§ 
— искомая медиана
§ — нижняя граница интервала, который содержит медиану
§ — величина интервала
§ 
— сумма частот или число членов ряда
§ 
- сумма накопленных частот интервалов, предшествующих медианному
§ — частота медианного интервала
Средние величины широко применяются в различных отраслях знаний. Особо важную роль они играют в экономике и статистике: при анализе, планировании, прогнозировании, при расчете нормативов и при оценке достигнутого уровня. Средняя всегда именованная величина и имеет ту же размерность, что и отдельная единица совокупности