Дисперсия – наиболее общая мера вариации признака. На основании дисперсии можно увидеть количество, меру влияния всех причин на вариацию признака. Можно видеть те причины, которые в наибольшей мере вызывают вариацию признака.
Общая дисперсия 
характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий. 
Межгрупповая дисперсия 
измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
— групповые средние,
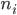— численность единиц i -й группы
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, неучитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
— дисперсия i-ой группы.
Все три дисперсии (
) связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
на этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации.
29. Структурные средние: мода, медиана, квартиль, дециль, смысл и применение для анализа распределений.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
где:
— значение моды
— нижняя граница модального интервала
— величина интервала
— частота модального интервала
— частота интервала, предшествующего модальному
— частота интервала, следующего за модальным
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот 
, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
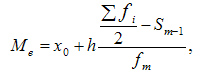
где:
— искомая медиана
— нижняя граница интервала, который содержит медиану
— величина интервала
— сумма частот или число членов ряда
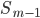- сумма накопленных частот интервалов, предшествующих медианному
— частота медианного интервала
Квартили предоставляют важную информацию о структуре вариационного ряда к-л признака. Вместе с медианой они делят вариационный ряд на 4 равные части. Квартилей две, их обозначают символами Q, верхняя и нижняя квартиль. 25% значений меньше, чем нижняя квартиль, 75% значений меньше, чем верхняя квартиль.
Квартили (четверти) отсекают от совокупности соответственно 25%, 50% и 75%.
Децили отсекают от совокупности соответственно 10%, 20%, 30% и т.д.