Вероятностный инструментарий оценки риска
Стандартные методики
Как выяснилось, риск – категория вероятностная, поэтому в процессе оценки неопределённости и количественного определения риска используют вероятностные расчёты. Важнейшим показателем, характеризующим меру финансового риска предприятия, является его уровень. Этот показатель оказывает определяющее воздействие на формирование уровня доходности финансовых операций предприятия — эти два показателя находятся в тесной взаимосвязи и представляют собой единую систему ”доходность – риск”. Соотношение уровня доходности и риска является одной из основных базовых концепций финансового риск-менеджмента, в соответствии с которой уровень доходности финансовых операций при прочих равных условиях всегда сопровождается повышением уровня их риска и наоборот [2, стр. 7].
Кроме того, уровень финансового риска является главным показателем оценки уровня финансовой безопасности предприятия, характеризующим степень защиты его финансовой деятельности от угроз внешнего и внутреннего характера. Поэтому оценка уровня риска в процессе управления финансовой деятельностью предприятия сопровождает подготовку практически всех управленческих решений.
Уровень финансового риска характеризует вероятность его возникновения под воздействием определенного фактора риска (или группы таких факторов) и возможных финансовых потерь при наступлении рискового события.
С учётом указанного определения формируется конкретный методический инструментарий оценки уровня риска, позволяющий решать связанные с ним конкретные задачи управления финансовой деятельностью предприятия. К числу основных расчётных показателей такой оценки относятся:
|
|
а) Уровень финансового риска. Он характеризует общий алгоритм оценки этого уровня, представленный следующей формулой:
где УР – уровень соответствующего финансового риска;
ВР – вероятность возникновения данного финансового риска;
РП – размер возможных финансовых потерь при реализации данного риска.
В практике использования этого алгоритма размер возможных финансовых потерь выражается обычно абсолютной суммой, а вероятность возникновения финансового риска – одним из коэффициентов измерения этой вероятности (коэффициентом вариации, бета-коэффициентом и др.). Соответственно уровень финансового риска при его расчёте по данному алгоритму будет выражен абсолютным показателем, что существенно снижает базу его сравнения при рассмотрении альтернативных вариантов.
б) Дисперсия. Она характеризует степень колеблемости изучаемого показателя (в данном случае – ожидаемого дохода от осуществления финансовой операции) по отношению к его средней величине. Чем колебания больше, тем выше степень риска. Расчёт дисперсии осуществляется по следующей формуле:
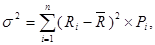
где σ2 – дисперсия;
Ri – конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой финансовой операции;
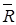- среднее ожидаемое значение дохода по рассматриваемой финансовой операции;
Рi – возможная частота (вероятность) получения отдельных вариантов ожидаемого дохода по финансовой операции;
n – число наблюдений.
Дисперсия не даёт полной картины линейных уклонений ΔX = X –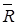 
, более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичным отклонениями с помощью известного неравенства Чебышева.
|
|
Вероятность того, что случайная величина X отклоняется от своего математического ожидания больше, чем на заданный допуск ε > 0, не превосходит её дисперсии, делённой на ε2, т.е.
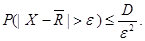
Отсюда видно, что незначительному риску по дисперсионному отклонению соответствует малый риск по линейным отклонения [6, стр. 106]: точки Х с большой вероятностью будут располагаться внутри ε – окрестности ожидаемого значения .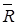
в) Среднеквадратическое (стандартное) отклонение. Этот показатель является одним из наиболее распространенных при оценке уровня индивидуального финансового риска, так же как и дисперсия определяющий степень абсолютной колеблемости и построенный на её основе. Он рассчитывается по следующей формуле [2, стр. 105]:
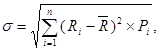
где σ – среднеквадратическое (стандартное) отклонение [2, стр. 106]. Среднеквадратическое отклонение σ является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак [6, стр. 105]. Как известно, среднеквадратическое отклонение имеет то неоспоримое достоинство, что при близости наблюдаемого распределения (например, распределении дохода от инвестиций) к нормальному, что, строго говоря, должно быть статистически проверено, этот параметр может быть использован для определения границ, в которых с заданной вероятностью следует ожидать значение случайной переменной. Так, например, с вероятностью 68,3% можно утверждать, что значение случайной переменной х (в нашем случае доход) находится в границах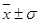 
, а с вероятностью 95,4% - в пределах 
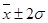, и т.д. [5, стр. 170]. Сказанное иллюстрируется на графике 1.
|
|
График №1
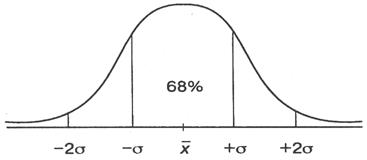
Соотношение площади под кривой нормального распределения в зависимости от расстояния от средней арифметической
Итак, будем считать, что риском операции называется число σ – среднеквадратическое отклонение управляемого фактора (например, дохода) Х операции, которое обозначим r = σ.
Если, например, под Х понимать случайный доход Q, то 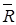Q представляет собой средний ожидаемый доход, или эффективность, а среднеквадратическое отклонение σQ является оценкой рискованности, риском и обозначается rQ.
г) Коэффициент вариации. Он позволяет определить уровень риска, если показатели среднего ожидаемого дохода от осуществления финансовых операций различаются между собой. Расчёт коэффициента вариации осуществляется по следующей формуле:
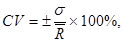
где CV – коэффициент вариации [2, стр. 108].
Коэффициент вариации V – безразмерная величина. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0% до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% - слабая колеблемость, 10-25% - умеренная колеблемость, свыше 25% - высокая колеблемость [6, стр. 106]. Пример расчёта показан в Приложении I.
д) Бета-коэффициент (или бета). Он позволяет оценить индивидуальный или портфельный систематический финансовый риск по отношению к уровню риска финансового рынка в целом. Этот показатель используется обычно для оценки рисков инвестирования в отдельные ценные бумаги. Расчёт этого показателя осуществляется по формуле:
где β – бета-коэффициент;
К – степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг (или по их портфелю) и средним уровнем доходности данной группы фондовых инструментов по рынку в целом [2, стр. 109];
σИ – среднеквадратическое отклонение доходности по индивидуальному виду ценных бумаг (или по их портфелю в целом);
σр – среднеквадратическое отклонение доходности по фондовому рынку в целом.
Уровень финансового риска отдельных ценных бумаг определяется на основе следующих значений бета-коэффициентов:
β = 1 – средний уровень;
β > 1 – высокий уровень;
β < 1 – низкий уровень [2, стр. 110].
С помощью вероятностного метода оценки риска можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом (проанализировав динамику её доходов) за некоторый промежуток времени. Выбор конкретных методов оценки определяется наличием необходимой информационной базы [2, стр. 103] и уровнем квалификации управленческого персонала.
2.1.2 “Стоимость под риском” [VAR]
Традиционные для практики финансового риск-менеджмента методы оценки меры риска на основе показателя его уровня имеют ряд недостатков. К числу основных из таких недостатков относится прежде всего то, что „уровневые" показатели риска не характеризуют максимально возможную сумму финансового ущерба при наступлении рискового события, а соответственно не позволяют и страховаться от финансового риска предприятия в полном его объёме. Кроме того, отдельные „уровневые” показатели не могут быть агрегированы по портфелю финансовых инструментов, обращающихся на различных видах финансового рынка (например, на валютном и фондовом), а также по различным инструментам даже одного вида финансового рынка (например, опциона и свопа). Наконец, использование „уровневых" показателей меры финансового риска в процессе его контроля на предприятии является недостаточно надёжным по таким финансовым инструментам, которые чувствительны к различным факторам риска.
В связи с этим в последнее десятилетие получила развитие новая методология оценки меры финансового риска на основе использования показателя “стоимость риска” или “стоимость под риском” [value-at-risk, VAR]. Начало внедрения этой новой методологии оценки меры риска в практику связывается с директивой Европейского совета от 1993 г. (ЕЕС-6-9З), предписывающей финансовым институтам (в первую очередь банкам, инвестиционным и страховым компаниям) устанавливать обязательное резервирование капитала для обеспечения рыночных (систематических) финансовых рисков на основе расчёта показателя VAR по предложенной им методике. Впоследствии (в 1995 г.) Базельский комитет по надзору за банками [2, стр. 114] разрешил коммерческим банкам применять собственный методический инструментарий расчета показателя VAR.
За прошедшее десятилетие оценка меры финансового риска на основе показателя VAR получила развитие в США и Западной Европе не только в среде финансовых институтов, но и в значительном числе компаний, функционирующих в реальном секторе экономики. Кроме того методический инструментарий оценки “стоимости под риском” [VAR] начал использоваться западными компаниями для исследования не только рыночного (систематического) риска, но и риска несистематического (в частности, для оценки кредитного риска). В последние годы использование этого показателя получает развитие и в нашей стране.
Рассмотрим основное содержание концепции и методический инструментарий оценки меры финансового риска на основе показателя VAR.
“Стоимость под риском” [VAR] представляет собой показатель статистической оценки выраженного в денежной форме максимально возможного размера финансовых потерь при установленном виде распределения вероятности факторов, влияющих на стоимость активов (инструментов), а также заданном уровне вероятности возникновения этих потерь на протяжении расчетного периода времени.
Из приведённого определения видно, что основу методологии расчёта показателя „стоимость под риском" [VAR] составляют три основных элемента.
Одним из таких элементов является установленный риск-менеджером вид распределения вероятностей рисковых факторов, влияющих на стоимость активов (инструментов) или их совокупного портфеля. Такими видами могут быть нормальное распределение, распределение Лапласа, Стьюдента и другие. Поэтому для определения используемого вида распределения вероятностей предварительно должно быть проведено статистическое исследование влияния изменения рискового фактора на изменение стоимости отдельного актива или всего их портфеля. На основе такого статистического исследования должна быть построена функция ценообразования актива (или портфеля) в зависимости от конкретного фактора (вида) финансового риска. Если же показатель VAR определяется по всей совокупности факторов риска (например, при оценке систематического риска в целом), то в этом случае следует определить форму и тесноту корреляционных связей между различными факторами риска. Корректность устанавливаемого вида распределения вероятностей в модели расчёта показателя VAR прямо определяет правильность его значений [2, стр. 115].
Вторым элементом, который используется в статистической модели определения показателя „стоимость под риском" [VAR], является задаваемый риск-менеджером уровень вероятности того, что максимально возможный размер финансовых потерь не превысит расчётное значение этого показателя. В терминологии финансового риск-менеджмента такая заданная вероятность характеризуется термином довер ительный уровень [confidence level]. Конкретное значение доверительного уровня для модели расчета показателя VAR выбирается риск-менеджером исходя из его рисковых предпочтений. В современной практике финансового риск-менеджмента этот уровень устанавливается обычно в пределах 95-99%.
Наконец, третьим элементом модели определения показателя модели „стоимости риска" [VAR] является устанавливаемый риск-менеджером расчетный период времени его оценки (или конкретный временной горизонт в рамках которого оцениваются предстоящие возможные финансовые потери). В терминологии финансового риск-менеджмента такой отрезок времени характеризуется термином „период поддержания позиции” [holding реriod]. В современной практике финансового риск-менеджмента этот период определяют обычно по одному из следующих двух критериев: намечаемого периода владения рассматриваемым активом (т.е. времени его удержания в портфеле предприятия) или уровня его ликвидности (реального срока его конверсии в денежную форму без потери своей текущей рыночной стоимости).
Наглядное представление о формировании показателя VAR с учетом рассмотренных трех элементов его расчетной модели даёт график, представленный на графике 2.
Как видно из приведенного графика, кривая АВС иллюстрирует нормальный вид распределения вероятностей при6ыли и убытков по рассматриваемому финансовому инструменту в заданном расчётном периоде времени. Заштрихованное поле внутри этого графика (EFBC) соответствует избранному доверительному уровню (95% площади под кривой), а незаштрихованное поле (AFE) — характеризует значения возможных убытков, выходящие за рамки доверительного уровня (5%). На графике показатель VAR определён в сумме 15 усл. ден. ед., что соответствует максимальному размеру возможных финансовых потерь по рассматриваемому финансовому инструменту при заданных доверительном уровне и расчетном периоде оценки.
Современный методический инструментарий оценки „стоимости под риском” [VAR] использует ряд методов конкретных вычислений этого показателя.
График №2
Графический метод определения значения показателя „стоимость под риском” [VAR] [2, стр. 116]
Основными их этих методов являются:
1. Аналитический (или параметрический метод). Он исходит из предположения о нормальном распределении вероятностей рассматриваемых факторов риска и требует в процессе построения модели расчёта VAR только оценки параметров этого распределения. После такой оценки, основанной на результатах статистического исследования, вычисление показателя VAR осуществляется путем умножения полученных стандартных отклонений на соответствующий избранному доверительному уровню расчетный коэффициент (система таких коэффициентов для каждого доверительного уровня определена математическим путём и представлена в виде определенной таблицы вычислений). При определении на основе этого метода VAR для определённого портфеля финансовых инструментов необходимо дополнительно исследовать характер корреляционных связей между отдельными инструментами. Хотя этот метод и является наиболее простым, ареал его использования очень ограничен, так как в реальной практике параметрическое распределение вероятностей факторов финансового риска встречается довольно редко [2, стр. 117].
2. Метод исторического моделирования (или моделирование по историческим данным). Этот метод позволяет оценивать стоимость финансового риска за рамками нормального распределения вероятностей рассматриваемых факторов риска, но предполагает наличие обширной статистической базы данных по каждому из этих факторов. Он основан на предположении о стационарности колебаний конъюнктуры финансового рынка и генерируемых ими факторов риска, т.е. исходит из того, что на протяжении рассматриваемого периода поддержания позиции колебаниям конъюнктуры рынка будут присущи те же закономерности, что и в прошлом (историческим) периоде. Соответственно, в данном случае выдвигается только одна гипотеза о виде распределения вероятностей фактора риска (или их совокупности). По сравнению с аналитическим этот метод позволяет оценивать не только стандартные, но и весьма неординарные колебания конъюнктуры финансового рынка, т.е. полнее отражать реальные факторы риска.
З. Метод имитационного моделирования (или метод Монте-Карло). В основе этого метода лежит многократная (доходящая при достаточности компьютерных ресурсов до десятков тысяч вариантов) имитация условий генерирования факторов риска и их отражении на изменении стоимости отдельных финансовых инструментов или их совокупного портфеля. Такая имитация носит случайный характер, но в пределах заданных параметров. Такое искусственное моделирование факторов риска позволяет избирать любой вид распределения их вероятностей и позволяет достичь наибольшей точности расчетов стоимости под риском [VAR]. Кроме того, в отличие от метода исторического моделирования этот метод не связан с выбором конкретной ретроспективы.
4. Дерево решений имеет целью получить устойчивое решение. Эта задача во многом похожа на ту, которая встречается при анализе устойчивости решений, например в математическом программировании, и заключается в оценке того, как возможное изменение исходных условий скажется на полученном результате. Это вполне понятно, так как цель расчетов заключается отнюдь не в нахождении чисел, а в понимании условий, при которых эти числа ещё остаются верными [1, стр. 151].
Среди других методов оценки стоимости под риском [VAR], используемых в последние годы в практике финансового менеджмента, следует выделить также метод анализа сценариев и некоторые другие.
В заключение следует отметить, что оценка стоимости финансовых рисков на основе методологии расчета показателя VAR позволяет не только полнее определять меру этих рисков, но и использовать её для нейтрализации и контроля этих рисков на предприятии [2, стр.118].