Между определённостью и неопределённостью лежит случай принятия решения в условиях риска, когда можно оценить вероятность возникновения каждого возможного условия [6, стр. 109].
В случае стохастической неопределённости, по теории статистических решений [4, стр. 248], когда неуправляемым факторам (состояниям природы) поставлены в соответствие вероятности, заданные экспертно или вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша КБ (критерия Байеса) или минимума ожидаемого среднего риска КМОСР.
Лучшей стратегией игрока будет та, которая обеспечивает ему максимальный средний выигрыш по матрице выигрышей (см. таблицу 1, расшифровка переменных там же), т.е.
 (2.3.1)
(2.3.1)
Применительно к матрице рисков (матрице упущенных возможностей (выгод)) лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск
 (2.3.2)
(2.3.2)
Пример расчёта показан в Приложении II.
Когда говорится о среднем выигрыше или риске, то подразумевается многократное повторение процесса принятия решений, хотя реально требуемого количества повторений чаще всего может и не быть.
Вероятностная постановка задачи выбора оптимальных решений в экономике более адекватно отражает реальные ситуации. Поэтому применение вероятностных моделей во многих случаях позволяет уменьшить риск при выборе наиболее эффективных решений. Однако применение указанных моделей связано с необходимостью определения вероятностных характеристик анализируемых процессов (ситуаций). Это существенно усложняет решение рассматриваемых задач. Во многих случаях вероятностное распределение экономических показателей бывает неизвестным. Поэтому возникает необходимость определения предпочтительных альтернатив при условии, что вероятностные характеристики экономических показателей являются неизвестными.
В условиях полной неопределённости, когда вероятности рассматриваемых ситуаций неизвестны, можно пользоваться правилом Лапласа, заключающимся в том, что все неизвестные вероятности Pj считают равными. После этого выбор эффективного решения можно принимать или по критерию Байеса (2.3.1) или по критерию минимизации среднего риска (2.3.2). Подобный критерий принятия решения можно назвать принципом недостаточного обоснования Лапласа [6, стр.112].
Заключение
На основании проведённой работы можно сделать следующие выводы:
риск всегда связан с выбором определённых альтернатив и расчётом вероятности их результата;
так как наибольшую прибыль приносят, как правило, рыночные операции с повышенным риском, то риск нужно рассчитывать до максимально допустимого предела, корректируя систему действий с позиций наибольшей прибыли при наименьших затратах;
экономико-статистические методы составляют основу проведения оценки финансового риска;
опираясь на методы теории вероятностей и математической статистики, разработаны методы количественной оценки экономического риска, выбора оптимального решения и построения доверительных интервалов;
рисковая ситуация – это разновидность неопределённости, когда наступление событий вероятно и может быть определено, то есть в этом случае объективно существует возможность оценить вероятность событий, возникающих в результате деятельности;
особая роль в решении рисковых экономических ситуаций отводится самостоятельному принятию решения руководящим лицом, в руках которого инструмент снижения риска – это сокращение объёма потерь, для чего существует большая группа методов, связанных с подбором других операций, таких, чтобы суммарная операция имела наименьший риск;
преимуществом вероятностного метода в управлении финансовыми рисками является глубокая теоретическая база математических расчётов, а недостатком – необходимость большого числа исходных данных (чем больше массив, тем достовернее оценка риска);
многие методы предупреждения и снижения рисков, широко применяемы на практике, нуждаются в дальнейшем математическом описании и доказательстве и, возможно, будут в дальнейшем проанализированы с позиций теории вероятностей и математической статистики.
Список используемой литературы
1. Анализ финансовых решений в бизнесе: учебное пособие / В.М.Попов, С.И. Ляпунов. – М.:КНОРУС, 2007.
2. Бланк И.А. Управление финансовыми рисками: Учеб. курс. – К.: Ника-Центр, 2006.
3. Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: Учебное пособие. – СПб.: Питер, 2006.
4. Принятие финансовых решений: теория и практика / под ред. А.О. Левковича. – Минск: Изд-во Гревцова, 2007.
5. Четыркин Е.М. Финансовая математика: Учебник. – 6-ое изд., испр. – М.: Дело, 2006.
6. Шапкин А.С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. – 2-е изд. – М.: Издательско-торговая корпорация “Дашков и КО”, 2003.
Приложение I
Пример использования стандартного вероятностного метода оценки рисков
Сравним по риску вложения в акции трёх типов A, B, C, если каждая из них по своему откликается на возможные рыночные ситуации, достигая с известными вероятностями определённых значений доходности (таблица 2).
Таблица №2
| Тип акции | Ситуация 1 | Ситуация 2 | ||
| вероятность, в долях единицы | доходность, % | вероятность, в долях единицы | доходность, % | |
| A | 0,5 | 0,5 | ||
| B | 0,99 | 15,1 | 0,01 | 5,1 |
| C | 0,7 | 0,3 |
По формулам (2.1) находим для акции A:

для акции В:

для акции С:

Так как наименьшее значение коэффициента вариации имеем для акции В (6,63%), то и вложения в эту акцию наиболее предпочтительны, тем более, что и σВ = rВ = 0,995% наименьшее [6, стр. 107].
Приложение II
Пример использования вероятностного метода для принятия решения в условиях неполной неопределённости
Пусть матрица выигрышей (2.2) имеет вид:

тогда по формуле

строим матрицу рисков R [6, стр. 110]. Находим

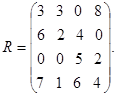
Предположим, что вероятности Pj равны: Pj= (1/2; 1/6; 1/6; 1/6). По формуле 2.3.2 находим средний ожидаемый риск:

Минимальный средний ожидаемый риск:
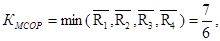
таким образом, по данному критерию оптимальной будет стратегия x3.
По формуле 2.3.1 найдём средний ожидаемый выигрыш
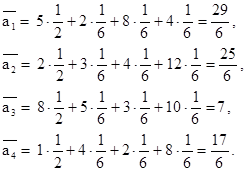
Максимальный средний ожидаемый доход

Таким образом, по критерию Байеса оптимальной будет также стратегия x3.