Наибольшее распространение получили логические элементы, реализующие комбинации: И – ИЛИ, И – НЕ, ИЛИ – НЕ, И – ИЛИ – НЕ.
Элемент И – НЕ (операция «штрих Шеффера») представляет собой элемент И с ин верстным выходом.
Элемент ИЛИ – НЕ выполняет логическую операцию, называемую «стрелка Пирса» и представляет схему ИЛИ с инверсным выходом.
По теореме Де Моргана: 
и 
, отсюда следует, что элемент И – НЕ выполняет функцию ИЛИ над инверсными значениями входных сигналов. Аналогично, элемент ИЛИ – НЕ реализует функцию И над инверсными значениями входных сигналов. Элементы И – НЕ и ИЛИ – НЕ, имеющие один вход, осуществляют операцию отрицания. Элемент И–ИЛИ–НЕ реализует инверсию функции, представленной в ДНФ, 
. Поскольку 
, то такой элемент позволяет получать КНФ от инверсных значений входных сигналов.
РЕАЛИЗАЦИЯ ПРАКТИЧЕСКОГО ЗАДАНИЯ
Цель работы
Изучить методы синтеза комбинационных схем в потенциальной системе элементов; получить навыки в сборке, наладке и экспериментальном исследовании синтезируемых схем.
2.2 Задание 1
а) Реализовать на базе "штрих Шеффера" логические элементы "И", "ИЛИ","НЕ".
б) Реализовать на базе "стрелка Пирса" логические элементы "И",
"ИЛИ","НЕ".
А) Элемент И:
|
Элемент ИЛИ:
|
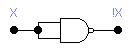Элемент НЕ:
|
Б) Элемент И: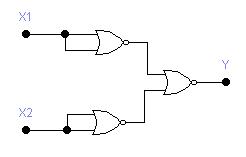 
|
Элемент ИЛИ: 
|
|
|
Элемент НЕ: 
|
Задание 2
Функция: 
+ 
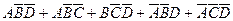
a) По заданной функции получить мин-ДНФ и реализовать ее в базисе
"И","ИЛИ","НЕ":
б) По заданной функции получить мин-ДНФ и реализовать ее в базисе
"штрих Шеффера".
в) По заданной функции получить мин-ДНФ и реализовать ее в базисе
"стрелка Пирса".
г) По заданной функции получить мин-КНФ и реализовать ее в базисе
"И","ИЛИ","НЕ".
д) По заданной функции получить мин-КНФ и реализовать ее в базисе
"штрих Шеффера".
е) По заданной функции получить мин-КНФ и реализовать ее в базисе
"стрелка Пирса".
СДНФ заданной функции, полученная путём развёртывания исходной функции.
Таблица истинности функции:
Таблица 1. Таблица истинности заданной функции.
Минимизируем СДНФ с помощью карт Карно
Таблица 2. Карта Карно для мин. ДНФ
| AB | |||||
| CD | |||||
Получаем мин. ДНФ 
Таблица 3. Карта Карно для мин. КНФ
| AB | |||||
| CD | |||||
и мин. КНФ 
Строим комбинационную схему в базисе И-ИЛИ-НЕ
Рисунок 7. мин ДНФ в базисе И-ИЛИ-НЕ
Преобразовываем мин. ДНФ в базис И-НЕ (штрих Шеффера):
Рисунок 8. мин ДНФ в базисе И-НЕ
|
|
Преобразовываем мин ДНФ в базис ИЛИ-НЕ (стрелка Пирса)
Рисунок 9. мин ДНФ в базисе ИЛИ-НЕ
Полученные комбинационные схемы имеют одинаковую таблицу истинности:
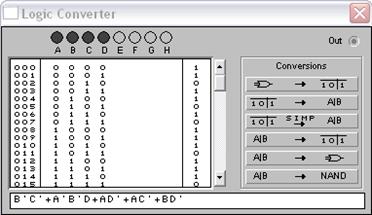
Рисунок 10. Таблица истинности мин. ДНФ
Теперь реализуем мин. КНФ. Для начала построим комбинационную схему в базисе И-ИЛИ-НЕ
Рисунок 11. мин КНФ в базисе И-ИЛИ-НЕ
Преобразуем мин КНФ в базис И-НЕ (штрих Шеффера):
Рисунок 12. мин КНФ в базисе И-НЕ
Преобразуем мин КНФ в базис ИЛИ-НЕ (стрелка Пирса):
Рисунок 13. мин КНФ в базисе ИЛИ-НЕ
Последние три комбинационные схемы имеют одну и ту же таблицу истинности и совпадает с таблицей истинности СДНФ:
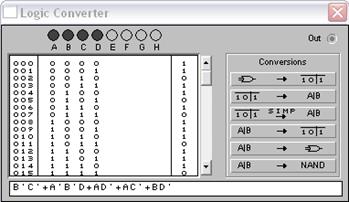
Рисунок 14. Таблица истинности мин. КНФ
ВЫВОД
Были изучены способы минимизации логических функций с помощь карт Карно и реализации их в базисах И-ИЛИ-НЕ, И-НЕ (штрих Шеффера), ИЛИ-НЕ (стрелка Пирса). Процесс минимизации позволяет значительно сократить затраты на логические элементы и повысить отказоустойчивость. Наиболее экономичными я считаю комбинационные схемы, реализованные в базисе И-НЕ, т.к. они содержат минимум логических элементов.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Конспект лекций по дисциплине «Прикладная Теория Цифровых Автоматов».
Методические указания по данной вычислительной работе.