Всякий ротор имеет множество дисбалансов, расположенных в различных плоскостях вращения. Выполняя уравновешивание ротора, можно было бы каждый из этих дисбалансов уменьшить до определённого значения. Для этого надо создавать в теле ротора дополнительные дисбалансы, направленные противоположно исходным дисбалансам, что обеспечивается постановкой дополнительных масс, которые называются корректирующими. Такой путь приводит к значительному увеличении массы ротора. Поэтому применим другой метод.
Выберем в роторе три плоскости: 
, 
(рис.2), перпендикулярные оси вращения. Подвижную систему координат 
поместим в плоскость .
рис2. Приведение неуравновешенности к двум плоскостям коррекции.
В этой плоскости на линии главного вектора дисбалансов 
находится центр масс ротора, он составляет угол 
с осью 
. Главный момент дисбалансов 
расположен в этой же плоскости , он приложен в центре приведения, т.е. в начале координат, и составляет угол 
с осью .
С учётом (2.10), (2.11) находим тригонометрические функции углов 
и :
Плоскости выбираются из конструктивных соображений и называются плоскостями коррекции. Вектор дисбаланса представим векторами 
, 
, расположенные в плоскостях коррекции, соблюдая условия:
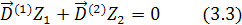
где 
- аппликаты плоскостей коррекции, с учётом их знаков.
В последнем выражении используются модули дисбалансов, а не векторы, т.к. три дисбаланса 
, 
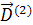параллельны.
С учётом (3.3), получаем:
Знаменатель 
представляет собой расстояние 
между плоскостями коррекции. Пару дисбалансов 
так же располагаем в плоскостях коррекции, соблюдая условие:
Вектор направлен перпендикулярно плоскости пары. Если смотреть с конца вектора , то момент пары должен быть положительным, т.е. направленным против часовой стрелки. Иначе говоря, вектор 
в одной из плоскостей составляет с осью угол 
, вектор 
в другой плоскости составляет с той же осью угол 
.
|
|
Складывая геометрически вектора 
, получим эквивалентный дисбаланс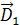 
в первой плоскости коррекции: 
Аналогично для второй плоскости коррекции (рис.2, 3):
рис.3 Эквивалентные дисбалансы и дисбалансы корректирующих масс.
Дисбалансы 
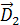развивают такие силы инерции:
Векторы этих сил 
совпадают по направлению с дисбалансами 
лишь при постоянной угловой скорости ротора. Эквивалентные дисбалансы в плоскостях коррекции оказывают на опоры ротора такое же силовое воздействие, что и векторы 
исходной неуравновешенности. Геометрическая сумма дисбалансов 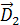должна ровняться вектору исходного дисбаланса :
Моменты дисбалансов относительно начала координат системы должны давать в сумме главный момент дисбалансов 
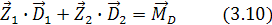
или в проекциях:
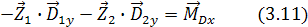
При статической неуравновешенности нет вектора , нет и векторов 
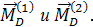
Остаётся вектор дисбаланса и эквивалентные ему дисбалансы 
в плоскостях коррекции. Эти три дисбаланса параллельны и направлены в одну сторону.
При моментной неуравновешенности нет вектора и нет векторов 
. Остаётся вектор 
и эквивалентные ему пара дисбалансов 
, которые равны по модулю и противоположны по направлению.
При динамической неуравновешенности есть оба вектора: и . Эквивалентные дисбалансы расположены в плоскостях коррекции произвольно (рис. 2).
|
|
Уравновешивание ротора.
Любой из видов неуравновешенности можно устранить двумя корректирующими массами, расположенными в двух плоскостях коррекции, как показано на рис.3. На этом рисунке изображены те же плоскости коррекции , , но в другой проекции. В плоскости нет дисбаланса и момента дисбалансов , т.к. они представлены эквивалентными дисбалансами в плоскостях коррекции . Дисбалансы составляют углы 
с осью r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> . На продолжении линий дисбалансов с противоположной стороны установлены корректирующие массы 
. Углы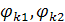 
называются углами коррекции, они отличаются от углов на 
, т.е.
Корректирующие массы должны быть такой же величины и установлены на таких же эксцентриситетах, чтобы их дисбалансы по модулю были равны расчётным дисбалансам: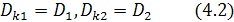 
Выполнение условий (4.1), (4.2) позволяет уравновесить ротор динамически двумя корректирующими массами. Уравновешенный таким способом ротор не будет при вращении оказывать динамических воздействий на свои опоры как при постоянной, так и при переменной угловой скорости.
Балансировка роторов.
Следует различать балансировку ротора при известном расположении неуравновешенных масс и случай, кода распределение масснеизвестно.