XII УРАВНОВЕШИВАНИЕ РОТОРОВ
В машиностроении и приборостроении любое вращающееся тело называют ротором (шкивы, зубчатые колеса, звездочки цепных передач, соединительные муфты, маховики, диски сцепления, шлифовальные круги, колеса автомобиля, диски турбин и т.п.). Роторы многих приборов вращаются с частотой 75 тысяч об/мин; роторы центрифуг, предназначенных для получения биологических эмульсий, имеют частоту вращения 500 тысяч об/мин. При конструировании таких роторовнеобходимо решить задачи динамического синтеза, связанные с распределением масс по условиям уменьшения динамических реакций в опорах ротора.
Статическая неуравновешенность ротора
Рассмотрим двухопорный ротор, вращающийся относительно оси 
(рис. 1) с угловой скоростью 
и угловым ускорением 
.
В точках 
, 
расположены опоры ротора. Выберем систему координат 
, вращающуюся вместе с ротором. Положение элементарной массы 
в теле ротора определим радиус-вектором 
, проведенным из начала координат.
Положение этой массы можно характеризовать и вектором 
, который является кратчайшим расстоянием до оси вращения. Вектор называется эксцентриситетом неуравновешенной массы. Произведение массы на ее эксцентриситет называется элементарным дисбалансом, 
.
Элементарный дисбаланс направлен по эксцентриситету. Через 
обозначены проекции динамических реакций в опорах ротора.
Из механики известно выражение для силы инерции элементарной массы:
Распишем проекции векторов, входящих в выражение (1.1):
Для проекций вектора 
получим:
Интегрируя по всему объему, определим проекции силы инерции:
где 
- координаты центра масс ротора; 
- масса ротора.
|
|
Далее получаем модуль вектора:
Произведение массы ротора на эксцентриситет его центра масс называется дисбалансом ротора 
. Вектор 
называется главным вектором сил инерции ротора, он приложен в его центре масс S.
Таким образом, статическая неуравновешенность ротора характеризуется наличием дисбаланса его массы или смещением центра масс с оси вращения. Возникающий при этом вектор в общем случае не совпадает по направлению с вектором дисбаланса 
. При постоянной частоте вращения направления этих векторов совпадают.
Моментная неуравновешенность ротора.
Момент силы инерции элементарной массы относительно начала координат находим из выражения:
С учётом (1.2), (1.3) получаем его проекции:
Проинтегрировав в проекциях, найдём:
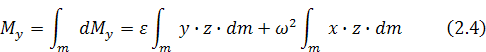
Интегралы в последних выражениях представляют собой центробежные 
и осевой 
моменты инерции. Получаем:
Модуль главного момента 
сил инерции ротора находится из выражения:
Где 
– модуль главного момента дисбалансов ротора.
Таким образом, моментная неуравновешенность ротора характеризуется наличием главного момента дисбалансов, направленного перпендикулярно оси вращения.
Величина и направление главного вектора сил инерции не зависит от центра приведения элементарных сил, а величина и направление главного момента сил инерции зависит (на рис.1 он приложен в точке 
).
Для выделения проекций массово-геометрических характеристик из проекций силовых (1.4), (1.5) и моментных характеристик (2.6), (2.7), достаточно принять 
(аналог скорости, безразмерная величина) и 
(аналог ускорения). При этих условиях получим:
|
|
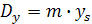(2.10)
; 
(2.11)
Если равны нулю массогеометрические характеристики: 
;
, то нулю равны главный вектор сил инерции, и главный момент сил инерции ротора.
Следовательно, условия, при которых проекции динамических реакций в опорах ротора будут равны нулю, запишутся в виде:
Это означает, что ось вращения ротора должна быть главной центральной осью. Момент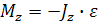 
непосредственно на динамические реакции не влияет, и его можно не принимать во внимание.
Виды неуравновешенности ротора можно различать по его массогеометрическим характеристикам:
- при статической неуравновешенности ротора
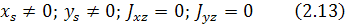
При моментной неуравновешенности
При динамической неуравновешенности
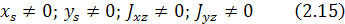
Итак, неуравновешенность - это состояние ротора, отличающееся таким распределением масс, которое во время вращения вызывает переменные нагрузки в опорах ротора. Мерой статической неуравновешенности является дисбаланс ротора 
, мерой моментной неуравновешенности - главный вектор дисбаланса 
.