Определение и свойства криволинейного интеграла I типа
Пусть функция z = f (M) определена вдоль некоторой кривой L, лежащей в плоскости XOY, то есть любой точке MÎL соответствует f (M). Пусть y = j (x) - уравнение кривой L, где j (x) - непрерывно-дифференцируемая функция. Тогда кривая L будет гладкой и спрямляемой. A, B - концы кривой L. Разобьем кривую произвольным образом на n частей точками A=M 0, M 1,…, Mn=B. На каждой частичной дуге 

 выберем произвольно точку
выберем произвольно точку  . Составим сумму
. Составим сумму
 , (1)
, (1)
где 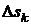 - длина дуги
- длина дуги  .
.
Эта сумма называется интегральной суммой для функции z = f (M), заданной на кривой L. Обозначим  .
.
Определение. Если существует конечный предел при l ®0 интегральной суммы (1), не зависящий ни от способа разбиения кривой L на части, ни от выбора точек  , то он называется криволинейным интегралом I типа (или криволинейным интегралом по длине дуги) от функции f (M) по кривой L и обозначается
, то он называется криволинейным интегралом I типа (или криволинейным интегралом по длине дуги) от функции f (M) по кривой L и обозначается  или
или  .
.
Функция f (M) называется интегрируемой вдоль кривой L.
Свойства криволинейного интеграла I типа
1º. Величина криволинейного интеграла не зависит от направления интегрирования:

(это объясняется тем, что при составлении интегральной суммы (1) нумерация точек разбиения может быть произведена и в обратном порядке: от В к А, это ничего не меняет).
2º. (Аддитивность)

 .
.
3º. (Линейность)
 .
.
2. Задача о площади цилиндрической поверхности
Как известно, определенный интеграл  геометрически представляет собой площадь криволинейной трапеции, ограниченной кривой y = f (x), осью
геометрически представляет собой площадь криволинейной трапеции, ограниченной кривой y = f (x), осью  и прямыми x=a, x=b. Если f (x)£0, площадь надо взять со знаком «-». Аналогично можно прийти к геометрическому смыслу криволинейного интеграла I типа.
и прямыми x=a, x=b. Если f (x)£0, площадь надо взять со знаком «-». Аналогично можно прийти к геометрическому смыслу криволинейного интеграла I типа.
Пусть в плоскости  дана спрямляемая кривая L=АВ, на которой определена функция f (M)³0. Тогда точки (M; f (M)) образуют некоторую кривую, которая лежит на цилиндрической поверхности с направляющей L и образующей, параллельной
дана спрямляемая кривая L=АВ, на которой определена функция f (M)³0. Тогда точки (M; f (M)) образуют некоторую кривую, которая лежит на цилиндрической поверхности с направляющей L и образующей, параллельной  .
.
Задача. Определить площадь  части цилиндрической поверхности, которая ограничена сверху кривой z = f (M), снизу – кривой L, с боков – прямыми AA¢ и BB¢.
части цилиндрической поверхности, которая ограничена сверху кривой z = f (M), снизу – кривой L, с боков – прямыми AA¢ и BB¢.
 Для решения этой задачи разобьем кривую
Для решения этой задачи разобьем кривую 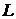 произвольно точками A=M 0, M 1,…, Mn=B на n частей. На каждой частичной дуге
произвольно точками A=M 0, M 1,…, Mn=B на n частей. На каждой частичной дуге 
 выберем произвольно точку
выберем произвольно точку  . Из каждой точки дробления
. Из каждой точки дробления  проведем прямые, параллельные оси
проведем прямые, параллельные оси  . Поверхность разобьется на n полосок
. Поверхность разобьется на n полосок 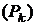 . Каждую такую полоску заменим прямоугольником с основанием
. Каждую такую полоску заменим прямоугольником с основанием 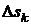 =
=  и высотой
и высотой  . Площадь ее
. Площадь ее  . Тогда
. Тогда
 . (2)
. (2)
Равенство (2) тем точнее, чем мельче разбиение кривой L на части. Пусть  . Тогда переходя к
. Тогда переходя к 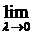 в (2), получим точное равенство:
в (2), получим точное равенство:
 .
.
Геометрический смысл криволинейного интеграла I типа
Из определения криволинейного интеграла I типа и этой задачи следует, что криволинейный интеграл  при f (M)³0 численно равен площади участка цилиндрической поверхности с образующей, параллельной O z, который снизу ограничен контурами интегрирования L=AB, а сверху - кривой z = f (M).
при f (M)³0 численно равен площади участка цилиндрической поверхности с образующей, параллельной O z, который снизу ограничен контурами интегрирования L=AB, а сверху - кривой z = f (M).
Если 
 , то
, то  ,
,
где  - длина самого контура интегрирования L.
- длина самого контура интегрирования L.
Таким образом, с помощью криволинейного интеграла I типа можно вычислить площадь цилиндрической поверхности и длину дуги.
3. Задача о массе кривой
Рассмотрим физическую задачу, которая приводит к понятию криволинейного интеграла I типа. Пусть вдоль некоторой спрямляемой кривой L распространена масса с плотностью r (М) " M Î L.
Задача. Определить массу  всей этой кривой.
всей этой кривой.
Разобьем кривую L на частичные дуги 
 . На каждой частичной дуге выберем произвольно точку
. На каждой частичной дуге выберем произвольно точку  ,
,  - плотность в точке
- плотность в точке  . Будем считать, что плотность на всей частичной дуге
. Будем считать, что плотность на всей частичной дуге  постоянна и равна
постоянна и равна  . Тогда
. Тогда  - масса дуги
- масса дуги  , следовательно,
, следовательно,  - масса всей кривой L.
- масса всей кривой L.
Последнее равенство тем точнее, чем меньше разбиение. Пусть  . Тогда
. Тогда
 .
.
Физический смысл криволинейного интеграла I типа
 физически выражает массу кривой L, плотность в каждой точке которой равна f (M).
физически выражает массу кривой L, плотность в каждой точке которой равна f (M).
4. Вычисление криволинейного интеграла I типа
Криволинейный интеграл I типа вычисляется путем сведения его к обыкновенному определенному интегралу. Пусть требуется вычислить  .
.
Теорема. Пусть кривая L=AB задана параметрически
 , (3)
, (3)
где j (t) и y (t) - непрерывно дифференцируемы на [ t 1; t 2]. Пусть f (x; y) непрерывна на кривой L. Тогда
 . (4)
. (4)
Доказательство.
 Пусть для определенности меньшему значению параметра t 1 соответствует точка A. Функция f (x; y) непрерывна вдоль кривой L, т. е. непрерывна в любой точке М (x; y)Î L. Положение точки
Пусть для определенности меньшему значению параметра t 1 соответствует точка A. Функция f (x; y) непрерывна вдоль кривой L, т. е. непрерывна в любой точке М (x; y)Î L. Положение точки  на кривой L определяется длиной дуги
на кривой L определяется длиной дуги  . Этим самым координаты x, y точки M тоже определяются как функции от s:
. Этим самым координаты x, y точки M тоже определяются как функции от s:  Это есть параметрическое представление кривой L с параметром s Î[0; S ], где S - длина всей кривой L. Тогда f (x; y)= f (x (s); y (s))= F (s) - сложная функция от s.
Это есть параметрическое представление кривой L с параметром s Î[0; S ], где S - длина всей кривой L. Тогда f (x; y)= f (x (s); y (s))= F (s) - сложная функция от s.
Пусть 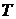 - произвольное разбиение кривой L на дуги
- произвольное разбиение кривой L на дуги  . Произвольно выберем на
. Произвольно выберем на 
 точку
точку  . Обозначим через
. Обозначим через  и
и  значения параметра s, отвечающие соответственно точкам
значения параметра s, отвечающие соответственно точкам  и
и  . Тогда
. Тогда
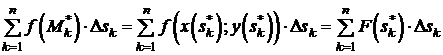 . (5)
. (5)
Справа в (5) – обычная интегральная сумма для функции F (s), где  . Переходя в (5) к
. Переходя в (5) к 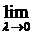
 , получим
, получим
 , (6)
, (6)
где интегрирование по s уже обозначает взятие обыкновенного определенного интеграла от функции одной переменной F (s). Так как f (x; y) непрерывна и x = x (s), y = y (s) непрерывны, то сложная функция F (s) непрерывна и, следовательно, существуют все интегралы в (6).
С другой стороны длину s дуги  можно рассматривать как функцию параметра t: s = s (t). Таким образом, M = M (j (t); y (t)). С возрастанием t от t 1 до t 2 величина s возрастает от 0 до S. Известно, что дифференциал дуги
можно рассматривать как функцию параметра t: s = s (t). Таким образом, M = M (j (t); y (t)). С возрастанием t от t 1 до t 2 величина s возрастает от 0 до S. Известно, что дифференциал дуги
 .
.
Выполнив замену переменной в (6) получим:
 =
=  .
. 
Замечание. Если кривая L задана явным уравнением y = j (x) (x Î[ a; b ], j (x)- непрерывно дифференцируемая функция), то принимая за параметр переменную  , получим параметрическое уравнение кривой:
, получим параметрическое уравнение кривой:  Следовательно,
Следовательно,
 . (7)
. (7)
 Пример 1. Вычислить
Пример 1. Вычислить  ,
, 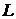 - дуга астроиды
- дуга астроиды 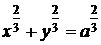 , лежащей в первой четверти.
, лежащей в первой четверти.
Δ Параметрическое уравнение части астроиды, лежащей в первой четверти: 
 ,
,  .
.
По формуле (4)



 . Δ
. Δ
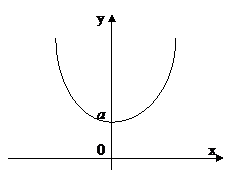 Пример 2. Вычислить массу всей цепной линии
Пример 2. Вычислить массу всей цепной линии  , если линейная плотность ее
, если линейная плотность ее  .
.
Δ  . Применим формулу (7):
. Применим формулу (7):
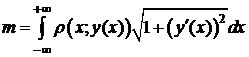 .
.
 ,
,  ,
,

 .
.
Следовательно,

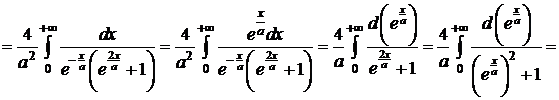

 . Δ
. Δ