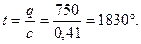Температуру газовых смесей можно определить по правилу смещения. Таким образом, сумма теплосодержаний отдельных компонентов до смешения должна быть равна общему теплосодержанию смеси, если при смешении не происходит никаких химических реакций. В этом случае компоненты могут и не принадлежать к различным газам, а лишь иметь различную начальную температуру.
Если объемы (или объемные доли) отдельных компонентов обозначить через u1,u2,u3..., температуры их через t 1, t 2, t 3... и т. д., средние теплоемкости через с 1, с 2, c 3... в интервале температур 0°— t 1, t 2, t 3, температуру смеси t, а теплоемкость компонентов в интервале температур 0—t через с 1', с 2', c 3', и т. д., то в соответствии с изложенным
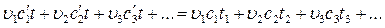 (1)
(1)
В левой части равенства сумма слагаемых представляет собой количество тепла, заключающееся в смеси, в правой — каждое слагаемое есть количество тепла, вносимое каждым компонентом.
Из этого равенства следует, что
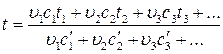 (2)
(2)
Трудность решения задачи заключается в том, что присутствующие в правой части равенства величины с 1', с 2', c 3'... суть функции от неизвестной, подлежащей определению величины t. Приближенное решение достигается одним из следующих способов.
Если известны t 1, t 2, t 3..., то принимается с 1'= с 1, с 2'= с 2, c 3'= с 3... и находят t; для найденного таким образом t выбирают теплоемкости с 1', с 2', c 3'... и т. д. и вновь находят t. Если расхождение между двумя таким образом найденными значениями невелико (порядка 50°), то последнее значение принимается за истинное. В противном случае расчет повторяют. Таким путем можно достигнуть нужной точности.
Второй способ приближенного решения задачи заключается в следующем. В равенстве
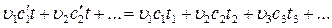 (3)
(3)
заменим произведения с ' t через i так, чтобы
с 1' t=i '1; с 2' t 1 =i '2;
с 1' t 1 =i '1; с 2' t 2 =i 2;
Таким образом,
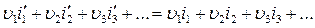 (4)
(4)
или
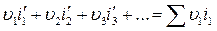 (5)
(5)
Стоящая в правой части сумма Su i задана.
Теплосодержания i 1', i 2', i 3'... соответствуют искомой температуре смеси. Значение последней должно удовлетворять тождеству Su i ' =Su i.
При решении задачи поступаем так. Задаемся каким-либо значением (t)1; для него подсчитываем S(u i ')1 и сравниваем суммой Su i. Если S(u i ') соответствующая (t)1 больше заданной Su i, то, следовательно, (t) выбрана выше истинной. Выбираем второе значение для t- (t)2 и для него находим сумму S(u i ')2. Если при этом
S(u i)1> 'Su i >S(u i ')2,
то искомая температура лежит между значениями (t)1 и (t)2.
Выбирая значения (t)1 и (t)2 так, чтобы разность (t)1 — (t)2 была возможно меньшей (практически 50° или 100°), можно истинное значение (t) найти путем интерполяции в этих пределах.
Пусть (t)1— (t)2 = 100° обозначим
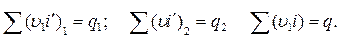
Повышению температуры смеси на (t)1—(t)2=100° соответствует увеличение количества, содержащегося в смеси тепла на q1—q2.
Очевидно, что искомому увеличению температуры смеси t-(t)2 =х0 соответствует изменение количества тепла, равное q—q2 из четырех величин 100, (q1—q2), x и (q — q2) составляем пропорцию, основываясь на предположении, что в интервале (t)1 и (t)2 теплоемкость постоянна. Тогда
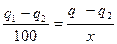
и
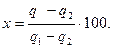
Следовательно,
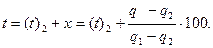
Эти весьма важные для определения температуры смеси газов методы поясним примерами.
Пример 1. К 1 нм3 продуктов сгорания топлива, содержащих 14,0% СO2; 5,5% H2O; 4,1% О2 и 76,4% N2 примешивается 0,5 м3 воздуха, Определить температуру смеси, если начальная температура продуктов сгорания 1000° и воздуха 50°.
Пользуясь первым из изложенных методов, имеем (уравнение 2):
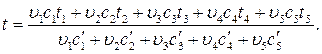
В этом случае
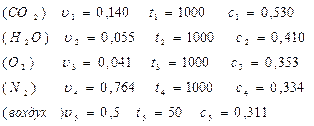
Принимая
с 1 =с 1', с 2= с 2', с 3= c 3' и т.д.
имеем
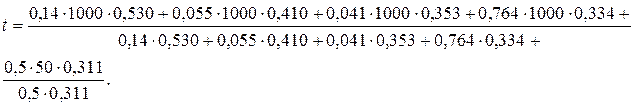
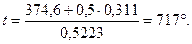
При этой температуре
с 1'=0,503; с 2'=0,390; с 3'=0,343; с 4'=0,324; с 5'=0,328.
Следовательно,
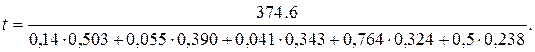
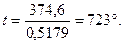
Последнее значение удовлетворительно, так как дальнейшие уточнения дадут изменение температуры менее чем на 2—3°,
Пример 2. Теплосодержание 1 нм3 продуктов сгорания торфа равно 750 ккал. Определить соответствующую данному теплосодержанию температуру, если состав продуктов сгорания по объему следующий: 16,0% СО2; 17,4% H2O; 66,6% N2
Пользуясь для решения этой задачи вторым методом, имеем:
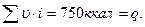
Задаемся (t)1= 1900°. Для этой температуры
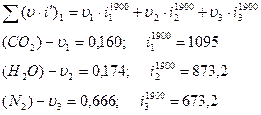
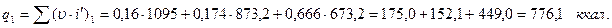
Так как
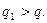
то
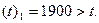
Задаемся
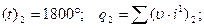
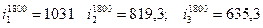
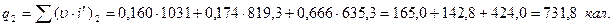
Следовательно, 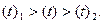
Интерполируя, находим
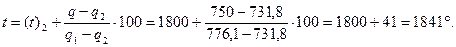
Искомая температура весьма просто может быть определена по формуле:
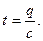
Принимая значение с средней теплоемкости продуктов сгорания торфа равным 0,41, определяем искомую температуру продуктом сгорания: