Достижению калориметрической температуры препятствует прежде всего то, что С02 и Н2О— продукты горения всякого топлива, независимо от его исходного состояния — являются сложными химическими соединениями, разлагающимися при -высоких температурах. Этот процесс диссоциации продуктов сгорания, количественно иллюстрируемый уравнениями
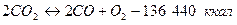 (18)
(18)
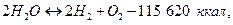 (19)
(19)
по существу является обратным процессу горения окиси углерода СO и водорода Н2. Таким образом, основные реакции горения суть обратимые реакции, для которых, как и для всяких химических реакций, между отдельными составными частями фазы или их физико-химическими характеристиками устанавливается некоторая зависимость, определяемая величиной так называемой константы равновесия..
Для интересующих нас процессов диссоциации СО2 и Н2О эти константы равновесия определяют величину отношений парциальных давлений исходных веществ и продуктов диссоциации. Для реакции диссоциации угольного ангидрида постоянная равновесия выражается следующим образом:
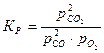 (20)
(20)
и для диссоциации водяного пара:
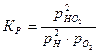 (21)
(21)
Величина постоянной равновесия зависит от температуры; теоретически эта зависимость определяется формулой Вант-Гоффа, практически же приходится пользоваться эмпирическими формулами, построенными по типу выражения, получаемого при интегрировании формулы Вант-Гоффа.
Для диссоциации СО2 формула Саккура устанавливает следующую зависимость постоянной равновесия от температуры:
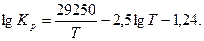 (22)
(22)
Для водяного пара:
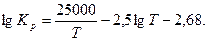 (23)
(23)
Если в качестве меры диссоциации принять отношение количества распавшегося вещества к количеству первоначального взятого (так называемый коэффициент диссоциации), то можно легко установить связь между константой равновесия и коэффициентом диссоциации.
Если обозначить:
а — коэффициент диссоциации CО2 или Н2О;
u— число молей избыточного кислорода • на 1 моль диссоциирующего газа;
z -число молей газов, не принимающих участия в реакции, отнесенное к 1 молю диссоциирующего газа;
Р — общее давление системы то
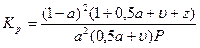 (24)
(24)
Для диссоциации чистых СО2 и Н2О в условиях, когда u =0 и z = 0, имеем:
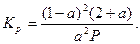 (25)
(25)
Последние уравнения в сочетании с предыдущими зависимостями Кр от Т дают уравнения равновесия, при помощи которых устанавливается связь между коэффициентом диссоциации и температурой.
Так как в результате диссоциации в продуктах сгорания появляются СО и Н2 наряду со свободным кислородом, то естественно, что количество сообщенного продуктам сгорания тепла меньше величины теплотворности топлива на величину теплоты горения продуктов диссоциации СО и Н2. В результате температура горения, определенная с учетом диссоциации, будет ниже температуры, определяемой без учета этого явления.
Температуру, до которой могут быть нагреты продукты сгорания топлива при частичной диссоциации угольного ангидрида и водяного пара, условимся называть теоретической температурой горения. Эта температура всегда ниже калориметрической. Теоретическая температура в большей или меньшей степени приближается к калориметрической. Из уравнений для определения константы равновесия следует, что с повышением температуры константа равновесия уменьшается; следовательно, уменьшается парциальное давление недиссоциировавшей двуокиси углерода и водяного пара. В результате расхождение между калориметрической температурой, определяемой в предположении, что диссоциация отсутствует, и теоретической, учитывающей ее влияние, увеличивается. Если при определении температуры продуктов сгорания исходить из равенства
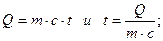 (26)
(26)
то влияние диссоциации скажется и в уменьшений Q и в изменении m. Обе эти величины зависят от степени диссоциации, т. е. от величины а — коэффициента диссоциации. Так как в уравнении равновесия и в уравнении калориметрическом величины а и t один и те же, то для определения теоретической температуры горения получаются два уравнения с двумя неизвестными — температурой и коэффициентом диссоциации.
Наиболее просто решение этой системы достигается графически — путем отыскания координат точки пересечения, двух кривых, построенных для каждого из уравнений. Первая кривая характеризует зависимость температуры от степени диссоциации; вторая дает зависимость коэффициента диссоциации от температуры.
Задача решается в следующем порядке. Задаваясь различными значениями коэффициента диссоциации, определяют соответствующую данному значению коэффициента диссоциации температуру продуктов сгорания. По полученным точкам строят в осях а —t кривую. Затем, задаваясь значениями температур; определяют из уравнения равновесия значения коэффициентом диссоциации. На той же сетке наносят новые данные. Пересечение двух кривых дает значения t и а, удовлетворяющие обоим уравнениям.
. Такой метод решения предложен акад. Н. С. Курнаковым и рекомендуется проф. Б. В. Старком как единственно возможный для случая, когда в продуктах сгорания присутствуют одновременно СО2, Н2О и О2.
Иллюстрируем примером этот метод определения теоретической температуры, используя некоторые данные из предыдущего расчета горения бензола.
В указанном расчете были определены:
1) начальное теплосодержание продукта сгорания to=900ккал/нм3
2) состав продуктов сгорания, если диссоциация отсутствует:
% Доли
СО2................. 16,1 0,161
Н2О................. 8,1 0,081
N2............... ... 75,8 0,758
100,0 1,000
3) калориметрическая температура горения tк= 22190. Для определения теоретической температуры необходимо учитывать, что в продуктах сгорания одновременно; присутствуют СО2 и Н2О, так что должно установиться равновесие между пятью составными частями.
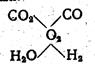
Следовательно, при решении задачи необходимо учитывать наличие трех неизвестных—температуры tm, коэффициента диссоциаций СО2 —х и коэффициента диссоциации Н2О—у. Трем неизвестным соответствуюти три уравнения:
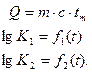
Последнее уравнение можно изменить новым, получающимся путем вычитания второго из третьего и деления полученного равенства на 2,
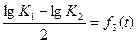
Левая часть этого равенства не что иное, как логарифм постоянной равновесия К3 реакций
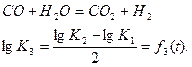
Значение этой постоянной, как и логарифмов постоянных К1 и K2, приведены в табл. 1.
Состав продуктов горения при диссоциации СО2 и Н2О выразится следующим образом:
СО2................. 0,161(1-х)............ =0,161-0,161х
СО................. 0,161х................=0,161х
Н2О................. 0,081(1-у).............=0,081-0,081у
Н2...................0,081у................ =0,081у
О2...................0,5×0,161х+0,5×0,081у....=0,08х+0,04у
N2...................0,758................. =0,758
S=1,0+0,08х+0,04у
Следовательно,
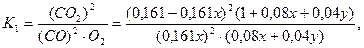
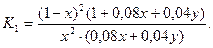
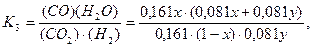
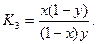
Отсюда
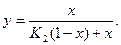
Таблица 1 Значения постоянной K3 и логарифмов постоянных К1 и К2
| Температура t, °C | LgH2 (2CO2«2CO+O2) | lgH2 (2H2O«2H2+O2) | H2(CO+H2O=CO2+H2) | Температура t, °C | LgH2 (2CO2«2CO+O2) | lgH2 (2H2O«2H2+O2) | H2(CO+H2O=CO2+H2) |
| 13,975 | 14,557 | 1,871 | 4,578 | 6,448 | 5,039 | ||
| 12,220 | 13,044 | 2,095 | 3,878 | 5,842 | 5,481 | ||
| 10,696 | 11,732 | 2,420 | 3,236 | 5,287 | 5,970 | ||
| 9,363 | 10,606 | 2,820 | 2,648 | 4,777 | 6,522 | ||
| 8,185 | 9,564 | 3,240 | 2,105 | 4,306 | 7,160 | ||
| 7,134 | 8,659 | 3,620 | 1,602 | 3,870 | 7,918 | ||
| 6,204 | 7,8846 | 4,220 | 1,135 | 3,465 | 8,835 | ||
| 5,347 | 7,113 | 4,621 | 0,701 | 3,089 | 9,961 |
Задаемся температурой равновесия 2000°, для которой
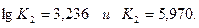
Принимаем х = 0,180, тогда
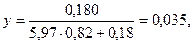
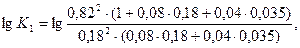
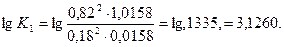
Принимаем х = 0,16, тогда
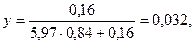
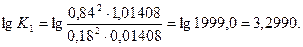
Для интерполяции находим:
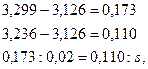
откуда
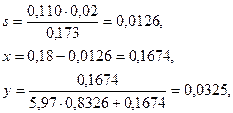
Находим температуру, соответствующую
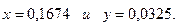
Состав продуктов сгорания:
СО2 0,161(1-0,1674).................... =0,1338 13,15
СО 0,161×0,1174.......................=0,0280 2,76
Н2О 0,081(1-0,0325).....................=0,0783 7,70
Н2 0,081×0,0325....................... =0,0027 0,27
О2 0,5×0,161×0,1674+0,5×0,081×0,0325......=0,017 1,67
N2 0,758............................. =0,758 74,45
S=1,0178 100,00
Тепло для нагрева продуктов сгорания:
горение бензола...... 
диссоциация СО2..... 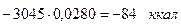
диссоциация Н2О..... 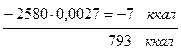
Теплосодержание i'продуктов сгорания при = 2000°.
СО2................................ =0,1315×1159=152,2 ккал/м3
СО.................................=0,0276×718,4=19,9 ккал/м3
Н2О................................ =0,0770×929,0=71,6 ккал/м3
Н2................................. =0,0027×672,0=1,8 ккал/м3
О2................................. =0,0167×751,5=12,5 ккал/м3
N2.................................=0,7445×712,2=531,0 ккал/м3
i'= 789,0 ккал/м3
Теплосодержание i''продуктов сгорания при t''=2100°
СО2................................ =0,1315×1224=166,0 ккал/м3
СО.................................=0,0276×758,1=20,9 ккал/м3
Н2О................................ =0,0770×985,8=76,0 ккал/м3
Н2................................. =0,0027×709,4=1,9 ккал/м3
О2................................. =0,0167×791,8=13,2 ккал/м3
N2.................................=0,7445×750,6=559,5 ккал/м3
i'= 837,5 ккал/м3
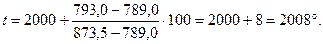
Так как температура получилась выше 2000° то искомая температура выше 2000 и ниже 2100°.
Задаемся температурой равновесия 2100°. Для этой температуры
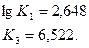
Принимаем х= 0,240, тогда
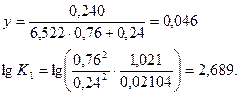
Принимаем х = 0,250, тогда
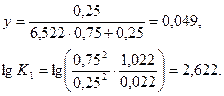
2,689-2,622=0,067
2,648-2,622=0,026
0,067:0,01=0,026:s,
откуда
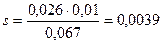
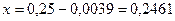
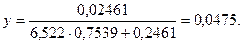
Находим температуру, соответствующую значениям:х=0,2461 и у=0,0475
состав и количество продуктов сгорания:
СО2 0,161(1-0,2461).................... =0,1212 11,86
СО 0,161×0,2461.......................=0,0396 3,88
Н2О 0,081(1-0,0475).....................=0,0770 7,53
Н2 0,081×0,0475....................... =0,0040 0,39
О2 0,5×0,161×0,2461+0,5×0,081×0,0475......=0,0217 2,12
N2 0,758............................. =0,758 74,22
S=1,0215 100,00
Тепло для нагрева продуктов сгорания:
горение бензола...... 
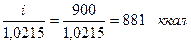
диссоциация СО2..... 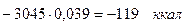
диссоциация Н2О..... 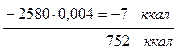
Теплосодержание продуктов сгорания i' при t' = 2000°
СО2................................ =0,1186×1159=137,2 ккал/м3
СО.................................=0,0388×718,4=27,9 ккал/м3
Н2О................................ =0,0753×929,0=70,0 ккал/м3
Н2................................. =0,0039×672,0=2,6 ккал/м3
О2................................. =0,0212×751,5=16,0 ккал/м3
N2.................................=0,7422×712,2=529,8 ккал/м3
i'= 783,5 ккал/м3
Теплосодержание продуктов сгорания i'' при t''=1900°
СО2................................ =0,1186×1095=129,8 ккал/м3
СО.................................=0,0388×680 =26,4 ккал/м3
Н2О................................ =0,0753×873,2=65,8 ккал/м3
Н2................................. =0,0039×635 =2,5 ккал/м3
О2................................. =0,0212×710,5=15,1 ккал/м3
N2.................................=0,7422×673,2=500,2 ккал/м3
i'= 739,8 ккал/м3
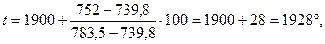
Сопоставляя полученные данные, имеем:
| х | у | tK | tP |
| 0,000 | 0,000 | ||
| 0,1674 | 0,0325 | ||
| 0,2461 | 0,0475 |
Истинное значение tm находим графически; для этого на миллиметровой бумаге в системе координат х — t строим две кривые: tк =f1 (x) и tp=f2 (х). Точка пересечения этих кривых и дает искомую температуру, Для нашего примера эта температура tm = 2004° (рис. 12). Ей соответствует х= 0,171. Для нахождения у строим две аналогичные кривые в системе координат у —t: tк=f1(y) и tp = f2 (у). Выполнив это (пунктирные кривые на рис. 3), найдём у=0,0332 и ту же температуру — tm = 2004°. При этих условиях будем иметь следующее.
Состав продуктов сгорания:
СО2 0,161(1-0,171)..................... =0,1335 11,86
СО 0,161×0,171........................=0,0275 3,88
Н2О 0,081(1-0,0332).....................=0,0783 7,53
Н2 0,081×0,0332...................... =0,0027 0,39
О2 0,5×(0,161×0,171 + 0,081×0,0332........=0,0151 2,12
N2 0,758............................. =0,758 0 74,6
S=1,0151 100,00
Теплосодержание продуктов сгорания:
горение бензола...... 
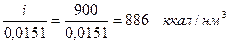
диссоциация СО2..... 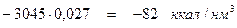
диссоциация Н2О..... 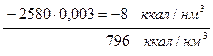
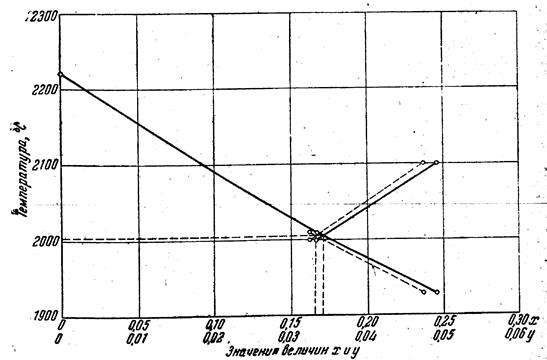
Рис. 3. График для подсчета температуры.
Приведенный пример показывает, что определение истинной теоретической температуры значительно сложнее определения калориметрической температуры без учета диссоциации.
Для облегчения расчетов по определению теоретической температуры горения составлена диаграмма (рис, 4), по которой можно быстро найти степень диссоциации углекислоты водяных паров в зависимости от температуры и парциального давления.
Быстро, хотя и менее точно, можно определить теоретические температуры с помощью I—t диаграммы.
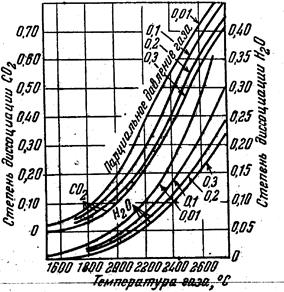
Рис. 4. Степень диссоциации углекислоты (СО2) и водяных паров (Н2О) в зависимости от температуры и парциального давления
Менее трудоемкая методика подсчета калориметрической и теоретической температур горения изложена в книге «Упрощенная методика теплотехнических расчетов».
В действительности же достигаемая температура горения может составлять лишь некоторую часть теоретической или калориметрической, если диссоциация незначительна. Определение действительной температуры горения топлива еще менее определенно, ибо требует, как было указано выше, учета влияния потерь тепла в окружающую среду за время горения.