Модульная арифметика
A
|
Версия для печати
< Лекция 1 || Лекция 2: 12345 || Лекция 3 >
Аннотация: Эта лекция необходима, чтобы подготовить читателя к дальнейшему разговору о криптографии. Лекция имеет несколько целей: рассмотреть арифметику целых чисел, которая базируется на теории делимости и нахождении наибольшего общего делителя, обратить внимание на важность модульной арифметики (арифметики над вычетами по модулю n) и операций в ней, потому что они широко используются в криптографии.
Ключевые слова: криптография, алгебраические, доказательство теорем, бинарная операция, делимое, алгоритм Евклида, частное решение, бинарный оператор
Криптография базируется на некоторых специфических областях математики, включая теорию чисел, линейную алгебру и алгебраические структуры. В этой лекции мы обсуждаем только те темы в вышеупомянутых областях, которые необходимы для понимания содержания следующих нескольких лекций. Читатели, которые знакомы с этими темами, могут пропустить лекцию полностью или частично. Подобные теоретические лекции встречаются всюду в этом курсе, когда это необходимо. Доказательства теорем и алгоритмов пропущены и даны только в приложении. Заинтересованный читатель может найти их в приложении Q.
Доказательства теорем и алгоритмов, обсуждаемых в этой лекции, можно просмотреть в приложении Q.
2.1. Арифметика целых чисел
В арифметике целых чисел мы используем множество целых чисел и несколько операций. Вы знакомы с этим множеством и соответствующими операциями, но они рассмотрены здесь, чтобы объяснить потом основы действий со сравнениями по модулю m.
Множество целых чисел
Множество целых чисел, обозначенных Z, содержит все числа (без дробей) от минус бесконечности до плюс бесконечности (рис. 2.1).
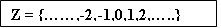
Рис. 2.1. Множество целых чисел
Бинарные операции
В криптографии нас интересует три бинарных операции в приложении к множеству целых чисел. Бинарные операции имеют два входа и один выход. Для целых чисел определены три общих бинарных операции — сложение, вычитание и умножение. Каждая из этих операций имеет два входа (a и b) и выход (c), как это показано на рис. 2.2. Два входа принимают числа из множества целых чисел; выход выводит результат операции — число из множества целых чисел.
Обращаем внимание, что деление не относится к этой категории операций, потому что мы скоро убедимся, что этой операции нужны два выхода вместо одного.
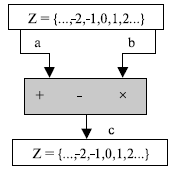
Рис. 2.2. Три бинарных операции для множества целых чисел
Пример 2.1
Следующие примеры показывают результаты трех бинарных операций на множестве двух целых чисел. Поскольку каждый вход может быть или положителен или отрицателен, мы имеем четыре случая для каждой операции.
Сложение 5+9=14 (-5)+9=4 5+(-9)=-4 (-5)+(-9)=-14
Вычитание 5-9=-4 (-5)-9=-14 5 - (-9)=14 (-5)- (-9)=+4
Умножение 5 x 9=45 (-5) x 9=-45 5 x (-9)=-45 (-5) x (-9)=45
Деление целых чисел
В арифметике целых чисел, если мы a делим на n, мы можем получить q и r. Отношения между этими четырьмя целыми числами можно показать как
В этом равенстве a называется делимое; q — частное; n — делитель и r — остаток. Обратите внимание, что это — не операция, поскольку результат деления a на n — это два целых числа, q и r. Мы будем называть это уравнением деления.
Пример 2.2
Предположим, что a = 255, а n = 23. Мы можем найти q = 11 и r = 2, используя алгоритм деления, мы знаем из элементарной арифметики — оно определяется, как показано на рис. 2.3.
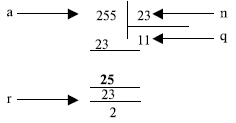
Рис. 2.3. Пример 2.2, нахождение частного и остатка
Большинство компьютерных языков может найти частное и остаток, используя заданные языком операторы. Например, на языке C оператор "/" может найти частное, а оператор "%" — остаток.
Два ограничения
Когда мы используем вышеупомянутое уравнение деления в криптографии, мы налагаем два ограничения. Первое требование: чтобы делитель был положительным целым числом (n > 0). Второе требование: чтобы остаток был неотрицательным целым числом (r >= 0). Рисунок 2.4 показывает эти требования с двумя указанными ограничениями.
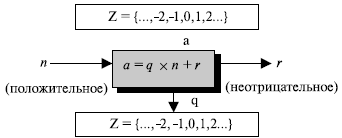
Рис. 2.4. Алгоритм деления целых чисел
Пример 2.3
Предположим, мы используем компьютер или калькулятор, а r и q отрицательны, при отрицательном a. Как можно сделать, чтобы выполнялось ограничение, что число r должно быть положительным? Решение простое: мы уменьшаем значение q на 1 и добавляем значение n к r, чтобы r стало положительным.
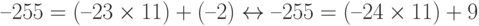
Мы уменьшили (–23), получили (–24) и добавили 11 к (–2), чтобы получить + 9. Полученное равенство эквивалентно исходному.
Граф уравнения деления
Мы можем изобразить рассмотренные выше уравнения с двумя ограничениями на n и r на рис. 2.5 с помощью двух графов. Первый показывает случай, когда число a положительно; второй — когда отрицательно.
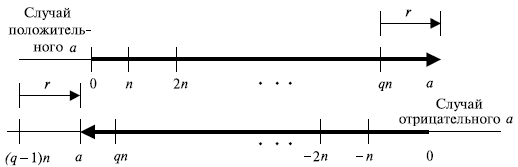
Рис. 2.5. Граф алгоритма деления
Граф начинается с нуля и показывает, как мы можем достигнуть точки, представляющей целое число a на линии. В случае положительного a мы должны перемещаться на величину 
направо и затем добавить дополнительную величину r в том же самом направлении. В случае отрицательного a мы должны двигаться на величину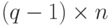 
налево (число q в этом случае отрицательно) и затем дополнять число r в противоположном для указанного выше движения направлении. В обоих случаях значение r положительно.
Теория делимости
Теперь кратко обсудим теорию делимости — тема, с которой мы часто сталкиваемся в криптографии. Если a не равно нулю, а r = 0, в равенстве деления мы имеем
a = q x n
Мы тогда говорим, что a делится на n (или n — делитель a). Мы можем также сказать, что a делится без остатка на n. Когда мы не интересуемся значением q, мы можем записать вышеупомянутые отношения как n|a. Если остаток не является нулевым, то n не делит, и мы можем записать отношения как n†a.
Пример 2.4
a. Целое число 4 делит целое число 32, потому что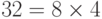 
. Это можно отобразить как 4|32. Число 8 не делит число 42, потому что 
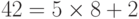. В этом уравнении число 2 — остаток. Это можно отобразить как 8†42.
Пример 2.5
а. Отображение делимости 13|78, 7|98, –6|24, 4|44, и 11 | (–33).
б. Отображение неделимости 13†27, 7†50, – 6†23, 4†41, и 11†(–32).
Свойства
Следующие несколько свойств теории делимости. Доказательства заинтересованный читатель может проверить в приложении Q.
Свойство 1: если a|1, то a=±1.
Свойство 2: если a|b и b|a, то a=±b
Свойство 3: если a|b и b|c, то a|c
Свойство 4: если a|b и a|c, то a|(m x b + n x c), где m и n — произвольные целые числа.
Пример 2.6
а. Если 3|15 и 15|45 то, согласно третьему свойству, 3|45.
б. Если 3|15 и 3|9, то, согласно четвертому свойству,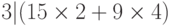 
, что означает 3|66.
Все делители
Положительное целое число может иметь больше чем один делитель. Например, целое число 32 имеет шесть делителей: 1, 2, 4, 8, 16 и 32. Мы можем упомянуть два интересных свойства делителей положительных целых чисел.
Свойство 1: целое число 1 имеет только один делитель — само себя.
Свойство 2: любое положительное целое число имеет по крайней мере два делителя — 1 и само себя (но может иметь больше).
Наибольший общий делитель
Одно целое число, часто необходимое в криптографии, — наибольший общий делитель двух положительных целых чисел. Два положительных целых числа могут иметь много общих делителей, но только один наибольший общий делитель. Например, общие делители чисел 12 и 140 есть 1, 2 и 4. Однако наибольший общий делитель — 4 (см. рис. 2.6).
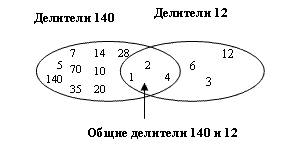
Рис. 2.6. Общие делители двух целых чисел
Наибольший общий делитель двух положительных целых чисел — наибольшее целое число, которое делит оба целых числа.
Алгоритм Евклида
Нахождение наибольшего общего делителя (НОД) двух положительных целых чисел путем составления списка всех общих делителей непригодно для достаточно больших чисел.
К счастью, больше чем 2000 лет назад математик по имени Эвклид разработал алгоритм, который может найти наибольший общий делитель двух положительных целых чисел. Алгоритм Евклида основан на следующих двух фактах (доказательство см. в приложении Q):
Факт 1: НОД (a, 0) = a
Факт 2: НОД (a, b) = НОД (b, r), где r — остаток от деления a на b
Первый факт говорит, что если второе целое число — 0, наибольший общий делитель равен первому числу. Второй факт позволяет нам изменять значение a на b, пока b не станет 0. Например, вычисляя НОД (36, 10), мы можем использовать второй факт несколько раз и один раз первый факт, как показано ниже.
НОД(36,10) = НОД(10,6) = НОД(6,4) = НОД(4,2) = НОД(2,0)
Другими словами, НОД (36, 10) = 2, НОД (10, 6) = 2, и так далее. Это означает, что вместо вычисления НОД (36, 10) мы можем найти НОД (2, 0). Рисунок 2.7 показывает, как мы используем вышеупомянутые два факта, чтобы вычислить НОД (a, b).
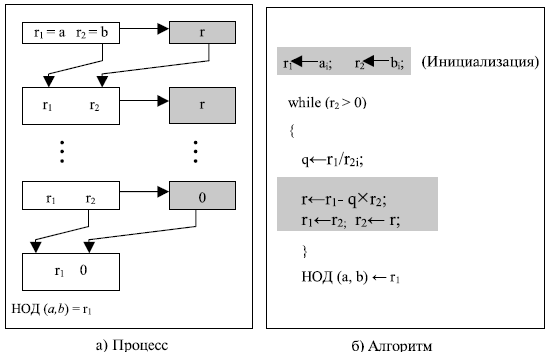
Рис. 2.7. Алгоритм Евклида
Для определения НОД мы используем две переменные, r1 и r2, чтобы запоминать изменяющиеся значения в течение всего процесса. Они имеют начальное значение a и b. На каждом шаге мы вычисляем остаток от деления r1 на r2 и храним результат в виде переменной r. Потом заменяем r1, на r2 и r2 на r и продолжаем шаги, пока r не станет равным 0. В этот момент процесс останавливается и НОД (a, b) равен r1.
Пример 2.7
Нужно найти наибольший общий делитель 2740 и 1760.
Решение
Применим вышеупомянутую процедуру, используя таблицу. Мы присваиваем начальное значение r1 2740 и r2 значение 1760. В таблице также показаны значения q на каждом шаге. Мы имеем НОД (2740, 1760) = 20.
| q | r1 | r2 | r |
Пример 2.8
Найти наибольший общий делитель 25 и 60.
Решение
Мы выбрали этот конкретный пример, чтобы показать, что для алгоритма Евклида безразлично, если первое число меньше, чем второе. Все равно мы получаем правильный ответ НОД (25, 60) = 5.
| q | r1 | r2 | R |
Расширенный алгоритм Евклида
Даны два целых числа a и b. Нам зачастую надо найти другие два целых числа, s и t, такие, которые
s x a + t x b = НОД(a,b)Расширенный алгоритм Евклида может вычислить НОД (a, b) и в то же самое время вычислить значения s и t. Алгоритм и процесс такого вычисления показан на рис. 2.8.
Здесь расширенный алгоритм Евклида использует те же самые шаги, что и простой алгоритм Евклида. Однако в каждом шаге мы применяем три группы вычислений вместо одной. Алгоритм использует три набора переменных: r, s и t.
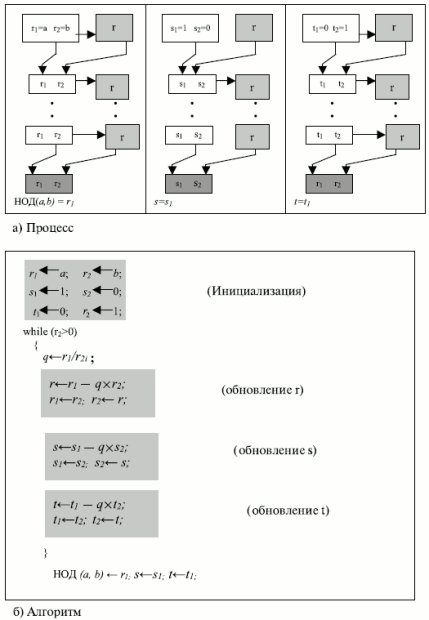
увеличить изображение
Рис. 2.8. Расширенный алгоритм Евклида
На каждом шаге переменные r1, r2 и r используются так же, как в алгоритме Евклида. Переменным r1 и r2 присваиваются начальные значения a и b соответственно. Переменным s1 и s2 присваиваются начальные значения 1 и 0 соответственно. Переменным t1 и t2 присваиваются начальные значения 0 и 1, соответственно. Вычисления r, s и t одинаковы, но с одним отличием. Хотя r — остаток от деления r1 на r2, такого соответствия в других двух группах вычислений нет. Есть только одно частное, q, которое вычисляется как r1/r2 и используется для других двух вычислений.
Пример 2.9
Дано a = 161 и b = 28, надо найти НОД (a, b) и значения s и t.
Решение
r = r1 – q x r2 s = s1 – qs2 t = t1 – q x t2Для отображения алгоритма мы используем следующую таблицу:
| q | r1 | r2 | R | s1 | s2 | s | t1 | t2 | t |
| -5 | |||||||||
| -1 | -5 | ||||||||
| -1 | -5 | -23 | |||||||
| -1 | -23 |
Мы получаем НОД (161, 28) = 7, s = –1 и t = 6. Ответы могут быть проверены, как это показано ниже.
(–1) x 161 + 6 x 28 = 7Пример 2.10
Дано a = 17 и b = 0, найти НОД (a, b) и значения s и t.
Решение
Для отображения алгоритма мы используем таблицу.
| q | r1 | r2 | R | s1 | s2 | s | t1 | t2 | t |
Обратите внимание, что нам не надо вычислять q, r и s. Первое значение r2 соответствует условию завершения алгоритма. Мы получаем НОД (17, 0) = 17, s = 1 и t = 0. Это показывает, почему мы должны придавать начальные значения s1— 1 и t1 — 0. Ответы могут быть проверены так, как это показано ниже:
(1 x 17) + (0 x 0) = 17Пример 2.11
Даны a = 0 и b = 45, найти НОД (a, b) и значения s и t.
Решение
Для отображения алгоритма мы используем следующую таблицу:
| q | r1 | r2 | R | s1 | s2 | s | t1 | t2 | t |
Мы получаем НОД (0,45) = 45, s = 0 и t = 1. Отсюда ясно, что мы должны инициализировать s2 равным 0, а t2 — равным 1. Ответ может быть проверен, как это показано ниже:
(0 x 0) + (1 x 45) = 45