Линейные диофантовы уравнения

Хотя очень важное приложение расширенного алгоритма Евклида будет рассмотрено далее, здесь мы остановимся на другом приложении — "нахождение решения линейных диофантовых уравнений двух переменных", а именно, уравнения ax + by = c. Мы должны найти значения целых чисел для x и y, которые удовлетворяют этому уравнению. Этот тип уравнения либо не имеет решений, либо имеет бесконечное число решений. Пусть d = НОД (a, b). Если d†c, то уравнение не имеет решения. Если d|c, то мы имеем бесконечное число решений. Одно из них называется частным, остальные — общими.

Линейное диофантово уравнение — это уравнение двух переменных: ax + by = c.

Частное решение

Если d|c, то можно найти частное решение вышеупомянутого уравнения, используя следующие шаги.

1. Преобразуем уравнение к a₁x + b₁y = c₁, разделив обе части уравнения на d. Это возможно, потому, что d делит a, b, и c в соответствии с предположением.

2. Найти s и t в равенстве a₁s + b₁t = 1, используя расширенный алгоритм Евклида.

3. Частное решение может быть найдено:

Частное решение: X₀ = (c/d)s и y₀ = (c/d)t

Общие решения

После нахождения частного решения общие решения могут быть найдены:

Общие решения: x = x₀ + k(b/d) и y = y₀ – k(a/d), где k — целое число

Пример 2.12

Найти частные и общие решения уравнения 21x + 14y = 35.

Решение

Мы имеем d = НОД (21, 14) = 7. При 7|35 уравнение имеет бесконечное число решений. Мы можем разделить обе стороны уравнения на 7 и получим уравнение 3x + 2y = 5. Используя расширенный алгоритм Евклида, мы находим s и t, такие, что 3s + 2t = 1. Мы имеем S = 1 и t = –1. Решения будут следующие:

Частное решение: x₀ = 5 x 1=5 и y₀ = 5 x (–1) = -5 тогда 35/7 =5Общие: x = 5+ k x 2 y= –5 – k x 3 где k — целое

Поэтому решения будут следующие (5, –5), (7, –8), (9, –11)...

Мы можем легко проверить, что каждое из этих решений удовлетворяет первоначальному уравнению.

Пример 2.13

Рассмотрим очень интересное приложение решения диофантовых уравнений в реальной жизни. Мы хотим найти различные комбинации объектов, имеющих различные значения. Например, мы хотим обменять денежный чек 100$ на некоторое число банкнот 20$ и несколько банкнот по 5$. Имеется много вариантов, которые мы можем найти, решая соответствующее диофантово уравнение 20x + 5y = 100. Обозначим d = НОД (20, 5) = 5 и 5|100. Уравнение имеет бесконечное число решений, но в этом случае приемлемы только несколько из них (только те ответы, в которых и x и y являются неотрицательными целыми числами). Мы делим обе части уравнения на 5, чтобы получить 4x + y = 20, и решаем уравнение 4s + t = 1. Мы можем найти s = 0 и t = 1, используя расширенный алгоритм Эвклида. Частное решение: и . 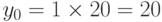Общие решения с неотрицательными x и y — (0, 20), (1, 16), (2, 12), (3, 8), (4, 4), (5, 0). Остальная часть решений неприемлема, потому что y становится отрицательным. Кассир в банке должен спросить, какую из вышеупомянутых комбинаций мы хотим. Первое число в скобках обозначает число банкнот по 20$; второе число обозначает число банкнот по 5$.

2.2. Модульная арифметика

Уравнение деления (), рассмотренное в предыдущей секции, имеет два входа (a и n) и два выхода (q и r). В модульной арифметике мы интересуемся только одним из выходов — остатком r. Мы не заботимся о частном q. Другими словами, когда мы делим a на n, мы интересуемся только тем, что значение остатка равно r. Это подразумевает, что мы можем представить изображение вышеупомянутого уравнения как бинарный оператор с двумя входами a и n и одним выходом r.

Операции по модулю

Вышеупомянутый бинарный оператор назван оператором по модулю и обозначается как mod. Второй вход (n) назван модулем. Вывод r назван вычетом. Рисунок 2.9 показывает отношение деления по сравнению с оператором по модулю.

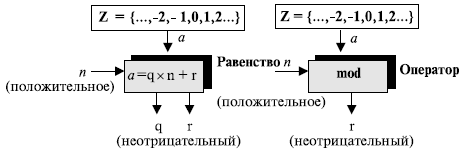
Рис. 2.9. Соотношение уравнения деления и оператора по модулю

Как показано на рис. 2.9, оператор по модулю (mod) выбирает целое число (a) из множества Z и положительный модуль (n). Оператор определяет неотрицательный остаток (r).

Мы можем сказать, что

a mod n = r

Пример 2.14

Найти результат следующих операций:

a. 27 mod 5

b. 36 mod 12

c. –18 mod 14

d. –7 mod 10

Решение

Мы ищем вычет r. Мы можем разделить a на n и найти q и r. Далее можно игнорировать q и сохранить r.

а. Разделим 27 на 5 - результат: r = 2. Это означает, что 27 mod 5 = 2.

б. Разделим 36 на 12 — результат: r = 0. Это означает, что 36 mod 12 = 0.

в. Разделим (–18) на 14 — результат: r = –4. Однако мы должны прибавить модуль (14), чтобы сделать остаток неотрицательным. Мы имеем r = –4 + 14 = 10. Это означает, что –18 mod 14 = 10.

г. Разделим (–7) на 10 — результат: r = –7. После добавления модуля –7 мы имеем r = 3. Это означает, что –7 mod 10 = 3.

Система вычетов: Zn

Результат операции по модулю n — всегда целое число между 0 и n - 1. Другими словами, результат a mod n — всегда неотрицательное целое число, меньшее, чем n. Мы можем сказать, что операция по модулю создает набор, который в модульной арифметике можно понимать как систему наименьших вычетов по модулю n, или Z_n. Однако мы должны помнить, что хотя существует только одно множество целых чисел (Z), мы имеем бесконечное число множеств вычетов (Z_n), но лишь одно для каждого значения n. Рисунок 2.10 показывает множество Z_n и три множества Z₂, Z₆ и Z₁₁.

Рис. 2.10. Некоторые наборы Zn

Сравнения

В криптографии мы часто используем понятие сравнения вместо равенства. Отображение Z в Z_n не отображаются "один в один". Бесконечные элементы множества Z могут быть отображены одним элементом Z_n. Например, результат 2 mod 10 = 2, 12 mod 10 = 2, 22 mod 10 = 2, и так далее. В модульной арифметике целые числа, подобные 2, 12, и 22, называются сравнимыми по модулю 10 (mod 10). Для того чтобы указать, что два целых числа сравнимы, мы используем оператор сравнения (). Мы добавляем mod n к правой стороне сравнения, чтобы определить значение модуля и сделать равенство правильным. Например, мы пишем:

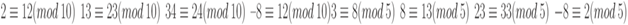
Рисунок 2.11 показывает принцип сравнения. Мы должны объяснить несколько положений.

a. Оператор сравнения напоминает оператор равенства, но между ними есть различия. Первое: оператор равенства отображает элемент Z самого на себя; оператор сравнения отображает элемент Z на элемент Z_n. Второе: оператор равенства показывает, что наборы слева и справа соответствуют друг другу "один в один", оператор сравнения — "многие — одному".

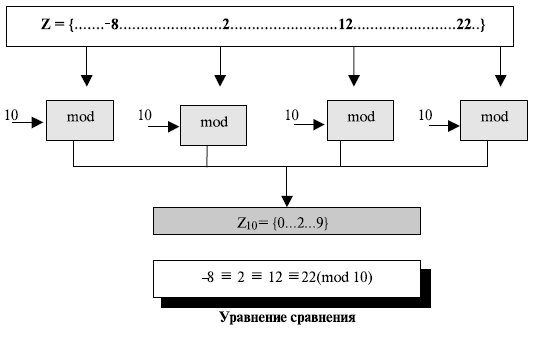
Рис. 2.11. Принцип сравнения

б. Обозначение (mod n), которое мы вставляем с правой стороны оператора сравнения, обозначает признак множества (Z_n). Мы должны добавить это обозначение, чтобы показать, какой модуль используется в отображении. Символ, используемый здесь, не имеет того же самого значения, как бинарный оператор в уравнении деления. Другими словами, символ mod в выражении 12 mod 10 — оператор; а сочетание (mod 10) в сравнении 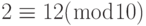означает, что набор — Z₁₀.

Система вычетов

Система вычетов [a], или [a]_n, — множество целых чисел, сравнимых по модулю n. Другими словами, это набор всех целых чисел, таких, что x = a (mod n). Например, если n = 5, мы имеем множество из пяти элементов [0], [1], [2], [3] и [4], таких как это показано ниже:

[0] = {…., –15, -10, –5, 0, 5, 10, 15, …}

[1] = {…., –14, –9, –4, 1, 6, 11, 16,…}

[2] = {…., –13, –8, –3, 2, 7, 12, 17,…}

[3] = {...., –12, –7, –2, 3, 8, 13, 18,…}

[4] = {…., –11, –6, –1, 4, 9, 14, 19,…}

Целые числа в наборе [0] все дают остаток 0 при делении на 5 (сравнимы по модулю 5). Целые числа в наборе [1] все дают остаток 1 при делении на 5 (сравнимы по модулю 5), и так далее. В каждом наборе есть один элемент, называемый наименьшим (неотрицательным) вычетом. В наборе [0] это элемент 0; в наборе [1] — 1, и так далее. Набор, который показывает все наименьшие вычеты: Z₅ = {0, 1, 2, 3, 4}. Другими словами, набор Z_n — набор всех наименьших вычетов по модулю n.

Круговая система обозначений

Понятие "сравнение" может быть лучше раскрыто при использовании круга в качестве модели. Так же, как мы применяем линию, чтобы показать распределение целых чисел в Z, мы можем использовать круг, чтобы показать распределение целых чисел в Z_n.

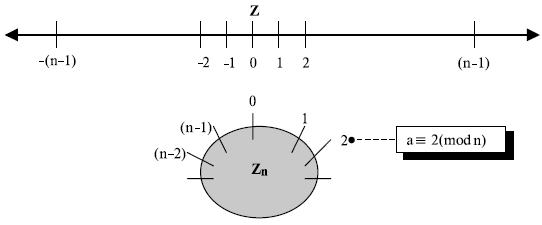
Рис. 2.12. Сравнение использования диаграмм для Z и Zn

Рисунок 2.12 позволяет сравнить два этих подхода. Целые числа от 0 до n–1 расположены равномерно вокруг круга. Все целые числа, сравнимые по модулю n, занимают одни и те же точки в круге. Положительные и отрицательные целые числа от Z отображаются в круге одним и тем же способом, соблюдая симметрию между ними.

Пример 2.15

Мы пользуемся сравнением по модулю в нашей ежедневной жизни; например, мы применяем часы, чтобы измерить время. Наша система часов использует арифметику по модулю 12. Однако вместо 0 мы берем отсечку 12, так что наша система часов начинается с 0 (или 12) и идет до 11. Поскольку наши сутки длятся 24 часа, мы считаем по кругу два раза и обозначаем первое вращение как утро до полудня, а второе — как вечер после полудня.

Операции в Zn

Три бинарных операции (сложение, вычитание и умножение), которые мы обсуждали для Z, могут также быть определены для набора Z_n. Результат, возможно, должен быть отображен в Z_n с использованием операции по модулю, как это показано на рис. 2.13.

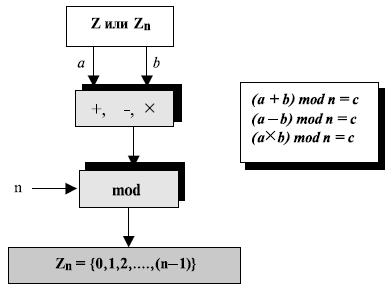
Рис. 2.13. Бинарные операции в Zn

Фактически применяются два набора операторов: первый набор — один из бинарных операторов ; второй — операторы по модулю. Мы должны использовать круглые скобки, чтобы подчеркнуть порядок работ. Как показано на рис. 2.13, входы (a и b) могут быть членами Z или Z_n.

Пример 2.16

Выполните следующие операторы (поступающие от Z_n):

а. Сложение 7 и 14 в Z₁₅

б. Вычитание 11 из 7 в Z₁₃

в. Умножение 11 на 7 в Z₂₀

Решение

Ниже показаны два шага для каждой операции:

(14+7) mod 15 -> (21) mod 15 = 6

(7–11) mod 13 -> (-4) mod 13 = 9

(7x11) mod 20 -> (77) mod 20 = 17

Пример 2.17

Выполните следующие операции (поступающие от Z_n):

a. Сложение 17 и 27 в Z₁₄

b. Вычитание 43 из 12 в Z₁₃

c. Умножение 123 на -10 в Z₁₉

Решение

Ниже показаны два шага для каждой операции:

(17 + 27) mod 14 -> (44) mod 14 = 2

(12 – 43) mod 13 -> (–31) mod 13 = 8

((123) x (–10)) mod 19 -> (–1230) mod 19 = 5

Свойства

Мы уже упоминали, что два входа для трех бинарных операторов в сравнении по модулю могут использовать данные из Z или Z_n. Следующие свойства позволяют нам сначала отображать два входа к Z_n (если они прибывают от Z) перед выполнением этих трех бинарных операторов . Заинтересованные читатели могут найти доказательства для этих свойств в приложении Q.

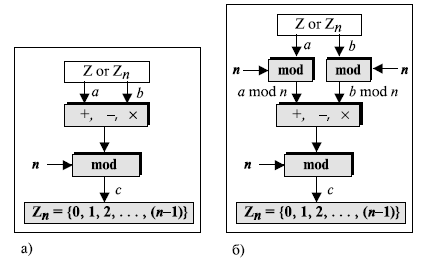
Рис. 2.14. Свойства оператора mod

Первое свойство: (a + b) mod n = [(a mod n) + (b mod n)] mod n

Второесвойство: (a – b) mod n = [(a mod n) - (b mod n)] mod n

Третьесвойство: (a x b) mod n = [(a mod n) x (b mod n)] mod n

Рисунок 2.14 показывает процесс до и после применения указанных выше свойств. Хотя по рисунку видно, что процесс с применением этих свойств более длинен, мы должны помнить, что в криптографии мы имеем дело с очень большими целыми числами. Например, если мы умножаем очень большое целое число на другое очень большое целое число, которое настолько большое, что не может быть записано в компьютере, то применение вышеупомянутых свойств позволяет уменьшить первые два операнда прежде, чем начать умножение. Другими словами, перечисленные свойства позволяют нам работать с меньшими числами. Этот факт станет понятнее при обсуждении экспоненциальных операций в последующих лекциях.

Пример 2.18

Следующие примеры показывают приложение вышеупомянутых свойств.

1.

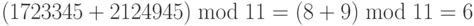
2.

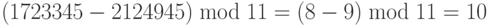
3.

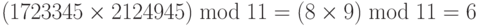
Пример 2.19

В арифметике мы часто должны находить остаток от степеней числа 10 при делении на целое число. Например, мы должны найти 10 mod 3, 10²mod 3, 10³mod 3, и так далее. Мы также должны найти 10 mod 7, 10²mod 7, 10³mod 7, и так далее. Третье свойство модульных операторов, упомянутое выше, делает жизнь намного проще.

10ⁿmod x = (10 mod x)ⁿ Применение третьего свойства n раз.

Мыимеем

10 mod 3 = 1 -> 10ⁿ mod 3 = (10 mod 3)ⁿ = 1

10 mod 9 = 1 -> 10ⁿ mod 9 = (10 mod 9)ⁿ = 1

10 mod 7 = 3 -> 10ⁿ mod 7 = (10 mod 7)ⁿ = 3ⁿ mod 7

Пример 2.20

Мы уже говорили, что в арифметике остаток от целого числа, разделенного на 3, такой же, как остаток от деления суммы его десятичных цифр. Другими словами, остаток от деления 6371 равен остатку от деления суммы его цифр (17), на 3. Мы можем доказать, что это утверждение использует свойства модульного оператора. Запишем целое число как сумму его цифр, умноженных на степени 10.

a = a_n10ⁿ +………+ a₁10¹ + a₀10⁰

Например: 6371 = 6 x 10³ + 3 x 10²+ 7 x 10¹+ 1 x 10⁰

Теперь мы можем применить модульную операцию к двум сторонам равенства и использовать результат предыдущего примера, где остаток 10ⁿmod 3 равен 1.

a mod 3 = (a_n x 10ⁿ +…+ a₁ x 10¹+ a₀ x 10⁰) mod 3

= (a_n x 10ⁿ) mod 3 +…+ (a₁ x 10¹) mod 3 + (a₀ x 10⁰ mod 3) mod 3

= (a_n mod 3) x (10ⁿ mod 3) +…+ (a₁ mod 3) x (10¹ mod 3) +

(a₀ mod 3) x (10⁰ mod 3) mod 3

= ((a_n mod 3) +…+ (a₁ mod 3) + (a₀ mod 3)) mod 3

= (a_n +…+ a₁ + a₀) mod 3

Инверсии

Когда мы работаем в модульной арифметике, нам часто нужно найти операцию, которая позволяет вычислить величину, обратную заданному числу. Мы обычно ищем аддитивную инверсию (оператор, обратный сложению) или мультипликативную инверсию (оператор, обратный умножению).

Аддитивная инверсия

В Z_n два числа a и b аддитивно инверсны друг другу, если b = n – a. Например,

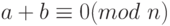
В Z_n аддитивная инверсия числу a может быть вычислена как b = n – a. Например, аддитивная инверсия 4 в Z₁₀ равна 10 – 4 = 6.

В модульной арифметике каждое целое число имеет аддитивную инверсию. Сумма целого числа и его аддитивной инверсии сравнима с 0 по модулю n.

Обратите внимание, что в модульной арифметике каждое число имеет аддитивную инверсию, и эта инверсия уникальна; каждое число имеет одну и только одну аддитивную инверсию. Однако инверсия числа может быть непосредственно тем же самым числом.

Пример 2.21

Найдите все взаимно обратные пары по сложению в Z₁₀.

Решение

Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4.