Сложение и умножение таблиц

Рисунок 2.16 показывает две таблицы для сложения и умножения. При сложении таблиц каждое целое число имеет аддитивную инверсию. Обратные пары могут быть найдены, если результат их сложения — ноль. Мы имеем (0, 0), (1, 9), (2, 8), (3, 7), (4, 6) и (5, 5). При умножении таблиц мы получаем только три мультипликативных пары (1, 1), (3, 7) и (9, 9). Пары могут быть найдены, когда результат умножения равен 1. Обе таблицы симметричны по диагонали, от левой вершины к нижней вершине справа. При этом можно обнаружить свойства коммутативности для сложения и умножения (a+b = b+a и ). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.

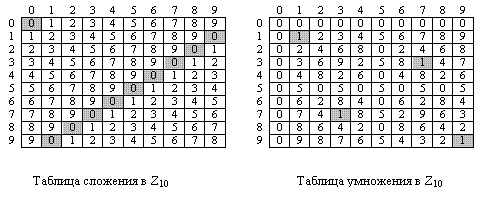
Рис. 2.16. Таблицы сложения и умножения для Z10

Различные множества для сложения и умножения

В криптографии мы часто работаем с инверсиями. Если отправитель посылает целое число (например, ключ для шифрования слова), приемник применяет инверсию этого целого числа (например, ключ декодирования). Если это действие (алгоритм шифрования/декодирования) является сложением, множество Z_n может быть использовано как множество возможных ключей, потому что каждое целое число в этом множестве имеет аддитивную инверсию. С другой стороны, если действие (алгоритм шифрования/декодирования) — умножение, Z_n не может быть множеством возможных ключей, потому что только некоторые члены этого множества имеют мультипликативную инверсию. Нам нужно другое множество, которое является подмножеством Z_n и включает в себя только целые числа, и при этом в Z_n они имеют уникальную мультипликативную инверсию. Это множество обозначается Z_n*. Рисунок 2.17 показывает некоторые случаи двух множеств. Обратите внимание, что множество Z_n* может быть получено из таблицы умножения типа показанной на рис. 2.16.

Каждый член Z_n имеет аддитивную инверсию, но только некоторые члены имеют мультипликативную инверсию. Каждый член Z_n* имеет мультипликативную инверсию, но только некоторые члены множества имеют аддитивную инверсию.

Мы должны использовать Z_n, когда необходимы аддитивные инверсии; мы должны использовать Z_n*, когда необходимы мультипликативные инверсии.

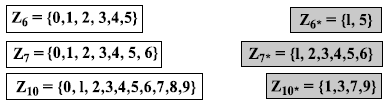
Рис. 2.17. Некоторые множества Zn и Zn*

Еще два множества

Криптография часто использует еще два множества: Z_p, и Z_p*. Модули в этих двух множествах — простые числа. Простые числа будут обсуждаться в следующих лекциях; пока можно сказать, что простое число имеет только два делителя: целое число 1 и само себя.

Множество Z_p — то же самое, что и Z_n, за исключением того, что n — простое число. Z_p содержит все целые числа от 0 до p – 1. Каждый элемент в Z_p имеет аддитивную инверсию; каждый элемент кроме 0 имеет мультипликативную инверсию.

Множество Z_p* — то же самое, что Z_n*, за исключением того, что Z_p* содержит все целые числа от 1 до p – 1. Каждый элемент в Z_p имеет аддитивную и мультипликативную инверсии. Z_p* очень хороший кандидат, когда мы нуждаемся во множестве, которое поддерживает аддитивную и мультипликативную инверсии.

Ниже показаны два множества, когда p = 13.