Мультипликативная инверсия

В Z_n два числа a и bмультипликативно инверсны друг другу, если

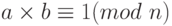
Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем .

В модульной арифметике целое число может или не может иметь мультипликативную инверсию. Целое число и его мультипликативная инверсия сравнимы с 1 по модулю n.

Может быть доказано, что a имеет мультипликативную инверсию в Z_n, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые.

Пример 2.22

Найти мультипликативную инверсию 8 в Z₁₀.

Решение

Мультипликативная инверсия не существует, потому что 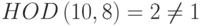. Другими словами, мы не можем найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.

Пример 2.23

Найти все мультипликативные инверсии в Z₁₀.

Решение

Есть только три пары, удовлетворяющие условиям существования мультипликативной инверсии: (1, 1), (3, 7) и (9, 9). Числа 0, 2, 4, 5, 6 и 8 не имеют мультипликативной инверсии.

Мы можем проверить, что

(1 x 1) mod 10 = 1 (3 x 7) mod 10 = 1 (9 x 9) mod 10 = 1

Пример 2.24

Найти все мультипликативные обратные пары в Z₁₁.

Решение

Мы имеем следующие пары: (1, 1), (2, 6), (3, 4), (5, 9), (7, 8) и (10, 10). При переходе от Z₁₀ к Z₁₁ число пар увеличивается. При Z₁₁НОД (11, a) = 1 (взаимно простые) для всех значений a, кроме 0. Это означает, что все целые числа от 1 до 10 имеют мультипликативные инверсии.

Целое число a в Z_n имеет мультипликативную инверсию тогда и только тогда, если НОД (n, a) = 1(mod n)

Расширенный алгоритм Евклида, который мы обсуждали ранее в этой лекции, может найти мультипликативную инверсию b в Z_n, когда даны n и b и инверсия существует. Для этого нам надо заменить первое целое число a на n (модуль). Далее мы можем утверждать, что алгоритм может найти s и t, такие, что 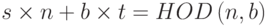. Однако если мультипликативная инверсия b существует, НОД (n, b) должен быть 1. Так что уравнение будет иметь вид

(s x n) + (b x t) = 1

Теперь мы применяем операции по модулю к обеим сторонам уравнения. Другими словами, мы отображаем каждую сторону к Z_n. Тогда мы будем иметь

(s x n + b x t) mod n =1 mod n[(s x n) mod n] + [(b x t) mod n] = 1 mod n0 + [(b x t) mod n ] = 1(b x t) mod n =1 -> Это означает, что t – это мультипликативная инверсия b в Z_n

Обратите внимание, что 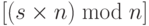на третьей строке — 0, потому что, если мы делим 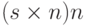, частное — s, а остаток — 0.

Расширенный алгоритм Евклида находит мультипликативные инверсии b в Z_n, когда даны n и b и НОД (n, b) = 1. Мультипликативная инверсия b — это значение t, отображенное в Z_n.

Рисунок 2.15 показывает, как мы находим мультипликативную инверсию числа, используя расширенный алгоритм Евклида.

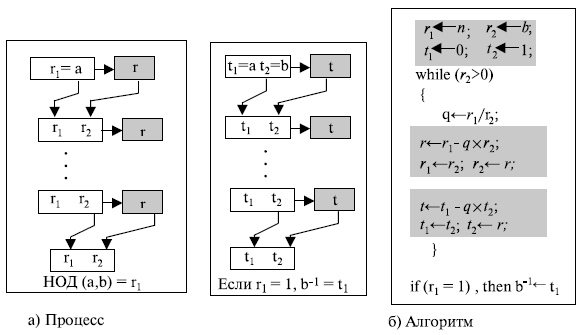
Рис. 2.15. Применение расширенного алгоритма Евклида для поиска мультипликативной инверсии

Пример 2.25

Найти мультипликативную инверсию 11 в Z₂₆.

Решение

Мы используем таблицу, аналогичную одной из тех, которые мы уже применяли прежде при данных r₁ = 26 и r₂ = 11. Нас интересует только значение t.

q	r1	r2	r	t1	t2	t
						-2
					-2
				-2		-7
					-7
				-7

НОД (26, 11) = 1, что означает, что мультипликативная инверсия 11 существует. Расширенный алгоритм Евклида дает t₁ = (–7).

Мультипликативная инверсия равна (–7) mod 26 = 19. Другими словами, 11 и 19 — мультипликативная инверсия в Z₂₆. Мы можем видеть, что .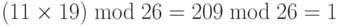

Пример 2.26

Найти мультипликативную инверсию 23 в Z₁₀₀.

Решение

Мы используем таблицу, подобную той, которую применяли до этого при r₁ = 100 и r₂ = 23. Нас интересует только значение t.

q	r1	r2	r	t1	t2	t
						-4
					-4
				-4		-13
					-13
				-13

НОД (100, 23) = 1, что означает, что инверсия 23 существует. Расширенный Евклидов алгоритм дает t₁ =-13. Инверсия — (–13) mod 100 = 87. Другими словами, 13 и 87 — мультипликативные инверсии в Z₁₀₀. Мы можем видеть, что .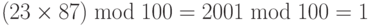

Пример 2.27

Найти мультипликативную инверсию 12 в Z₂₆.

Решение

Мы используем таблицу, подобную той, которую мы применяли раньше при r₁ = 26 и r₂ = 12.

q	r1	r2	r	t1	t2	t
					-2
				-2

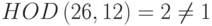, что означает отсутвствие для числа 12 мультипликативной инверсии в Z₂₆