Систематическая погрешность представляет собой определенную функцию влияющих факторов, состав которых зависит от физических, конструктивных и технологических особенностей СИ, условий их применения, а также индивидуальных качеств наблюдателя.
Для устранения постоянных систематических погрешностей применяют следующие методы:
Метод замещения, представляет собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений
Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.
Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдателями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.
Метод рандомизации - наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематическая погрешность каждого из них для всей совокупности являются разными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.
Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.
Анализ знаков неисправленных случайных погрешностей. Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.
Графический метод. Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.
Метод симметричных наблюдений. Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид у=kх+у  , где х, у - входная и выходная величина преобразователя; k - коэффициент, погрешность которого изменяется во времени по линейному закону; у
, где х, у - входная и выходная величина преобразователя; k - коэффициент, погрешность которого изменяется во времени по линейному закону; у  - постоянная.
- постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени Δt. При первом и третьем измерениях на вход преобразователя подается сигнал х  от образцовой меры. В результате измерений получается система уравнений:
от образцовой меры. В результате измерений получается система уравнений:
у 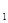 = kх
= kх  + у
+ у  ;
;
у  =(k+dk/dt* Δt)х+ у
=(k+dk/dt* Δt)х+ у  ;(36)
;(36)
у  =(k+2dk/dt* Δt)х
=(k+2dk/dt* Δt)х  + у
+ у  .
.
Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:
х=2 х  (у
(у  - у
- у  )/(у
)/(у 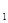 + у
+ у  -2 у
-2 у  )(37)
)(37)
Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и д.р. Рассмотрим подробнее дисперсионный анализ (критерий Фишера).
В практике измерений часто бывает необходимо объяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п.
После проведения N измерений их разбивают на s серий (s>3) по ni результатов наблюдений (sni = N) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии.
Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.
s  =1/(N-s) åå(x
=1/(N-s) åå(x  - x
- x  )
)  (38)
(38)
где x  =1/ ni å x
=1/ ni å x  ; x
; x  - результат i-го измерения в j-й серии.
- результат i-го измерения в j-й серии.
Внутрисерийная дисперсия s  характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние x
характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние x  различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия
различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия
s 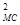
 =1/(1-s) å ni (x
=1/(1-s) å ni (x  -х)
-х)  (39)
(39)
где х=1/Nå ni x  , выражает силу действия фактора, вызывающего систематические различия между сериями.
, выражает силу действия фактора, вызывающего систематические различия между сериями.
Таким образом, s  /(s
/(s  -s
-s 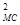 ) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а s
) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а s 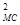 /(s
/(s 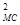 +s
+s  ) - долю дисперсии, обусловленную межсерийными различиями результатов наблюдений.
) - долю дисперсии, обусловленную межсерийными различиями результатов наблюдений.
Первую из них называют коэффициентом ошибки, вторую - показателям дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.
Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F=s 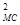 /s
/s  . Критическая область для критерия Фишера соответствует Р(F>F
. Критическая область для критерия Фишера соответствует Р(F>F  )=q.
)=q.
Значение F  для различных уровней значимости q, числа измерений N и числа серий s приложении 1[2], где к
для различных уровней значимости q, числа измерений N и числа серий s приложении 1[2], где к  = s-1. Если полученное значение критерия Фишера больше F
= s-1. Если полученное значение критерия Фишера больше F  (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
(при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
Решение
Определение наличия грубых погрешностей
Вычислим среднее арифметическое результатов наблюдений:
(40)
где xi - результат i-го измерения;- число наблюдений.
Вычисляем оценку среднего квадратического отклонения результата измерений по формуле:
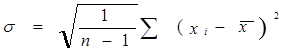 (41)
(41)
σ=1,348.
Определение наличия нормальных наблюдений (грубых погрешностей) используем правило 3 - х сигм:
| xi -х | ≤ 3σ (42)
Проверим крайние значения:
| 2 -4,734 | ≤ 3*1,1073
| 2,734 | ≤ 4,044 - выполняется
| 7 -4,734 | ≤ 3*1,1073
| 2,265 | ≤ 4,044 - выполняется
Если неравенства в крайних случаях выполняются, то и в остальных случаях они тоже выполняются. Т.к. все неравенства выполняются, то грубые погрешности отсутствуют.
Определение наличия систематических погрешностей
Для определения систематических погрешностей применим дисперсионный анализ (критерий Фишера).
| Для этого сначала разделим все измерения на 5серий.1 серия | 2 серия | 3 серия | 4 серия | 5 серия |
Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой по формуле 38.
s  =1/(N-s) åå(x
=1/(N-s) åå(x  - x
- x  )
)  ,
,
где x  =1/ ni å x
=1/ ni å x  ; x
; x  - результат i-го измерения в j-й серии.
- результат i-го измерения в j-й серии.
s  = 1,739135159
= 1,739135159
Усредненная межсерийная дисперсия по формуле 39
s 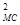
 =1/(1-s) å ni (x
=1/(1-s) å ni (x  -х)
-х) 
s 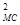
 = 0,201397497
= 0,201397497
Критерий Фишера F=s 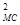 /s
/s  . Критическая область для критерия Фишера соответствует Р(F>F
. Критическая область для критерия Фишера соответствует Р(F>F  )=q. = 0,115803246.
)=q. = 0,115803246.
Для к 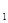 =s-1=4 и к
=s-1=4 и к  =N-s=59 по таблице имеем при
=N-s=59 по таблице имеем при  и при
и при 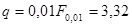 .
.
Полученное значение F меньше, чем 2,87 и 3,32. Следовательно, в результатах не обнаруживается наличия систематических ошибок.
Вычисление статистических характеристик и определение закона распределения результатов измерений
Первым шагом при идентификации закона распределения является построение по результатам измерений xi вариационного ряда (упорядоченной выборки). В вариационном ряду результаты измерений располагают в порядке возрастания.
Весь диапазон наблюдений значений x делится на интервалы, т.е. производится разделение ряда экспериментальных данных от наименьшего xmin до наибольшего xmax на i интервалов, и подсчитывают количество значений mi, приходящихся на каждый i-ый интервал. Это число делят на общее число наблюдений n и находят частоту, соответствующую данному интервалу по формуле 26:
= mi /n
Сумма частот всех интервалов должна быть равна единице.
Число интервалов можно подсчитать по формуле Старджесса:
= 1+3,32lgn (43)
= 1+3,32lg64 = 6,99832369
Принимаем число интервалов равное 7.
Длина интервала h вычисляется по формуле
= (xmax-xmin)/l (44)
h = (8-2)/7 = 0,857142857.
Принимаем длину интервалов равную 1.
Определим границы интервалов, частоту попадания в интервалы, середины интервалов и их статистические оценки:
Х0= Хmin=2;
Х1= Х0+ h=2+1=3;
Х2=Х1+h=3+1=4;
Х3= Х2+h=4+1=5;=X3+h=5+1=6;
Х5= Х4+h=6+1=7;
Х6= Х5 + h=7+1=8;
Находим середины интервалов:= (2+3)/2=2,5;= (3+4)/2=3,5;= (4+5)/2=4, 5;= (5+6)/2=5,5;= (6+7)/2=6,5;= (7+8)/2=7,5;= (8+9)/2=8,5.
Оформим полученные данные в таблицу 2.
Таблица 2
| № п/п | Интервал | Частота в интервале mi | Pi=mi/n | Среднее значение интервала zi | ziPi | Центрир. значение zi-mx | (zi-mx)2 | ((zi-mx)2)Pi | |
| 0,03125 | 2,5 | 0,078125 | -2,73438 | 7,476806641 | 0,233650208 | ||||
| 0,140625 | 3,5 | 0,492188 | -1,73438 | 3,008056641 | 0,423007965 | ||||
| 0,265625 | 4,5 | 1,195313 | -0,73438 | 0,539306641 | 0,143253326 | ||||
| 0,328125 | 5,5 | 1,804688 | 0,265625 | 0,070556641 | 0,023151398 | ||||
| 0,140625 | 6,5 | 0,914063 | 1,265625 | 1,601806641 | 0,225254059 | ||||
| 0,046875 | 7,5 | 0,351563 | 2,265625 | 5,133056641 | 0,24061203 | ||||
| 0,046875 | 8,5 | 0,398438 | 3,265625 | 10,66430664 | 0,499889374 | ||||
| Σ | 5,234375 | 1,788818359 |
Математическое ожидание: mx = Σ ziPi, (45)
= 5,234375;
Дисперсия: Dx = Σ(zi -mх)2Pi, (46)
= 1,788818359;
Среднее квадратическое отклонение: σx = √Dx, (47)
σx = 1,337467143;
Высчитаем оценку среднего квадратического отклонения среднего арифметического значения по формуле:
(48)
s = 0,167183393.
Определение принадлежности результатов измерений нормальному
Распределению
Приближенный метод проверки нормальности распределения
В качестве приближенного метода проверки нормальности распределения применяют метод, связанный с оценками центральных моментов третьего μ3 и четвертого μ4 порядков.
Для удобства сравнения подсчитывают безразмерные характеристики:
показатель асимметрии по формуле
А = (1/nσ3)Σ(xi-x)3, (49)
А = (1/64* 1,3374671433)[2(2- 4,734375)3+9(3- 4,734375)3+17(4- 4,734375)3+21(5- 4,734375)3+9(6- 4,734375)3+3(7- 4,734375)3+3*(8- 4,734375)3]= 0,424256458;
эксцесс о формуле
Е = (1/nσ4)Σ(xi-x)4, (50)
= (1/64* 1,3374671434)[2(2- 4,734375)4+9(3- 4,734375)4+17(4- 4,734375)4+21(5- 4,734375)4+9(6- 4,734375)4+3(7- 4,734375)4+3*(8- 4,734375)4]= 0,243936074.
Обе эти характеристики должны быть малы, если распределение нормально. О малости этих характеристик обычно судят по сравнению с их средними квадратическими ошибками:
для асимметрии по формуле
σА = √6(n-1)/[(n+1)(n+3)], (51)
σA = √6(64-1)/[(64+1)(64+3)] = 0,035434639;
для эксцесса по формуле
σЕ = √24n(n-2)(n-3)/[(n-1)2(n+3)(n+5)], (52)
σE = √24*64(64-2)(64-3)/[(64-1)2(64+3)(64+5)] = 0,064625234.
Если хотя бы одна из указанных характеристик по абсолютной величине значительно (в 2-3 раза) превосходит свою среднюю квадратическую ошибку, то нормальность закона распределения следует подвергнуть сомнению и провести более тщательный анализ результатов наблюдений.
А/ σA = 0,424256458/0,035434639 = 11,97293008;
E/ σЕ = 0,243936074/0,064625234 = 3,774625785.
Показатель эксцесса по абсолютной величине превосходит свою среднюю квадратическую ошибку в 3,8 раз, а показатель асимметрии - в 11,98 раз, поэтому следует провести более тщательный анализ результатов наблюдений.
Проверка нормальности распределения по критерию Пирсона (χ2)
Для проверки согласия между предполагаемым нормальным и эмпирическим распределением по критерию Пирсона (χ2) рекомендуется следующий порядок:
А) Результаты наблюдений группируются в интервальный вариационный ряд;
Б) Определяется длина и количество интервалов;
В) Подсчитывается количества mi наблюдений, находящихся в каждом из интервалов. Если в какой-либо интервал теоретически попадает меньше пяти наблюдений, то его соединяют с соседним интервалом;
Г) Нормируют случайную величину X, т.е. переходят к величине z = (x-mx)/σx и вычисляют концы интервалов (zi,zi+1) по формулам
zi = (xi-mx)/σx+1 = (xi+1-mx)/σx.
Причем наименьшее значение z, т.е. z1, полагают равным -∞, а наибольшее, т.е. z7, полагают равным +∞.
Д) Для каждого интервала вычисляется теоретическая вероятность попадания случайной величины в i-интервал по формуле
= F(zi+1)-F(zi),
где F - функция нормального распределения, равная
F(z) = Ф[(zв-mx)/σx] - Ф[(zн-mx)/ σx].
Здесь Ф - нормированная функция Лапласа (по таблице из [1]);в и zн - соответственно верхняя и нижняя границы i-го интервала.
Е) Определяется мера расхождения по формуле
На интервалы мы разделили ранее, результаты записаны в таблице 2.
Математическое ожидание:
mx= Σ (zi -mх)*Pi; (53)
= 5,234375;
Дисперсия:
Dx=Σ(zi -mх)2Pi; (54)
= 1,788818359;
Среднеквадратическое отклонение:
σ = √ Σ (zi -mx)2 Pi; (55)
σ = 1,337467143;
Для вычисления χ2 составим расчетную таблицу 3, объединив в ней интервалы, содержащие менее 5 попаданий.
Таблица 3 - Статистическая проверка гипотезы нормальности распределения результатов измерений
| п/п | Интервал (zi,zi+1) | Частота в интервале mi | zверх | zниж | Ф(zверх) | Ф(zнижн) | Pi | nPi | mi-nPi | (mi-nPi)2/ nPi | |
| -0,92292 | -2,41828 | -0,3212 | -0,4922 | 0,15 | 9,6 | 1,4 | 0,204166667 | ||||
| -0,17524 | -0,92292 | -0,714 | -0,3212 | 0,26 | 16,64 | 0,36 | 0,007788462 | ||||
| 0,572444 | -0,17524 | 0,2157 | -0,0714 | 0,4 | 25,6 | -4,6 | 0,8265625 | ||||
| 1,320126 | 0,572444 | 0,4066 | 0,2157 | 0,1 | 6,4 | 2,6 | 1,05625 | ||||
| 2,81549 | 1,320126 | 0,4976 | 0,4066 | 0,09 | 5,76 | 0,24 | 0,01 | ||||
| Σ | 2,104767628 |
Из таблицы 3 находим χ2 = 2,104767628;
Если полученное значение меньше табличного значения, взятого для числа степеней свободы k = l - s - 1 (где l- число объединенных интервалов, s- число наложенных связей), то различие между распределениями могут оказаться случайными (незначительными). В этом случае признается справедливой гипотеза о согласии эмпирического распределения с теоретическим.
При k = 4-2= 2, находим  = 4,6, при Р = 0,9.
= 4,6, при Р = 0,9.
Так как χ2 = 2,104767628 <4,6, то критерий Пирсона не противоречит принятой гипотезе о нормальном распределении результатов наблюдений.
Построение гистограммы и графика плотности распределения вероятности
Статистический ряд часто оформляется графически в виде так называемой гистограммы. Проведенные расчеты позволяют построить гистограмму. Гистограмма строится следующим образом. По оси абсцисс откладываются интервалы и на каждом из интервалов, как на основании, строится прямоугольник, площадь которого равна частоте данного интервала. Для построения гистограммы нужно частоту каждого интервала разделить на его длину и полученное число взять в качестве высоты прямоугольника.
Из способа построения гистограммы следует, что полная площадь ее равна единице. Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие интервалы, при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Эта кривая представляет собой график плотности распределения величины x, и по ее виду можно приближенно судить о законе распределения полученных измерений.
Для построения гистограммы заполним следующую таблицу.
Таблица 4
| п/п | zi | pi |
| 2,5 | 0,03125 | |
| 3,5 | 0,140625 | |
| 4,5 | 0,265625 | |
| 5,5 | 0,328125 | |
| 6,5 | 0,140625 | |
| 7,5 | 0,046875 | |
| 8,5 | 0,046875 |
Построим гистограмму.

Рисунок 4
Из способа построения гистограммы следует, что полная площадь ее равна единице. Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие интервалы, при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице.
Построим кривую нормально распределения для заданных результатов измерений, используя формулу:

где Хц - центр распределения, равный МО;
s - параметр рассеивания распределения, равный СКО.
Определение доверительных границ
Определим доверительные границы ε случайной погрешности результата измерений по формуле
ε = tqσx, (56)
где tq - коэффициент Стьюдента, определяемый по заданной доверительной вероятности P и числу наблюдений n.
Зададим доверительную вероятность P = 0,9, n = 64, тогда tq =1,6686.
ε = 1,6686∙0,9= 2,231697675.
Запись результата измерения
Результат измерения записывается в виде
=  x ± ε, (57)
x ± ε, (57)
= 4,734375±2,231697675.
Заключение
Используя критерий Пирсона, мы доказали принадлежность результатов измерений нормальному распределению.
Результат измерения (с доверительностью 0,9 и при количестве измерений N=64) представлен в следующем виде:= 4,73±2,23.
Список используемой литературы
1. Кузнецов Н.Д., Чистяков В.С. Сборник задач и вопросов по теплотехническим измерениям и приборам: Учеб. пособие.- М.: Энергия, 1978.- 216 с.
2. Назаров Н.Г. Метрология. Основные понятия и математические модели: Учеб. пособие для вузов / Н.Г. Назаров. - М.: Высш. шк., 2002. - 348 с.
. Сергеев А.Г., Крохин В.В. Метрология: Учеб. пособие для вузов.- М.: Логос, 2001.
. Шелепаев А.Г. Основы метрологии: Конспект лекций. - Новосибирск: НГАС, 1998 г.
. Шелепаев А.Г. Обработка результатов наблюдений при прямых измерениях: Метод. узакания - Новосибирск. НГАС, 1995.
. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений.- Л.: Энергоатомиздат. Ленингр. Отделение, 1985.-248 с.