Использование на практике вероятностного подхода к оценке погрешностей результатов измерений, прежде всего, предполагает знание аналитической модели закона распределения рассматриваемой погрешности. Встречающиеся в метрологии распределения достаточно разнообразны.
Множество законов распределения случайных величин, используемых в метрологии, целесообразно классифицировать следующим образом:
▪ трапецеидальные (плосковершинные) распределения. К ним относятся: равномерное, собственно трапецеидальное и треугольное (Симпсона);
▪ уплощенные (приблизительно плосковершинные) распределения;
▪ экспоненциальные распределения;
▪ семейство распределений Стьюдента;
▪ двухмодальные распределения.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Равномерное распределение описывается уравнением (рис 2):
, x < Xц- а, x > Xц +a;(x) =
/2a, Xц - a £ x £ Xц +a.(8)
Рисунок 2
Равномерное распределение имеет погрешности: квантования в цифровых приборов, округления при расчетах, отчета показаний стрелочного прибора, от трения в стрелочных приборах с креплением подвижной части на кернах и подпятниках, а также в самоуравновешивающихся мостах и потенциометрах со следящим электромеханическим приводом, погрешность определения момента времени для каждого из концов временного интервала в электронных цифровых хронометрах и частотомерах и т.д. Суммируясь между собой эти погрешности, образуют трапецеидальные распределения с различными отношениями сторон.
Свойства равномерного распределения:
Характеристическая функция Mx(t)= ebt-eat/(b-a)*t;(9)
Среднее μ = (b+a)/2;(10)
Дисперсия σ2= (b-a)2/12;(11)
Третий центральный момент μ3=0
Четвертый центральный момент μ4= (b-a)4/80;(12)
Коэффициент вариации ς= (b-a)/ √3(a+b);(13)
Коэффициент ассиметрии α3=0;
Коэффициент эксцесса α4= 1,8
Нормальное распределение (распределение Гаусса)
Оно получило наибольшее распространение
, (14)
где 
- параметр рассеивания распределение, равный среднеквадратическому отклонению (СКО); 
- центр распределения, равный математическому ожиданию (МО). Вид нормального распределения показан на рисунке 3.
Рисунок 3 - Нормальное распределение
Широкое использование нормального распределения на практике объясняется центральной предельной теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
При введении новой переменной 
получается нормированное нормальное распределение, интегральная и дифференциальная функции которого соответственно равны:
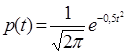(15)
Нормирование приводит к переносу начала координат в центр распределения и выражению абсциссы в долях СКО. Значения интегральной и дифференциальной функций нормированного нормального распределения сведены в таблицы, которые можно найти в литературе по теории вероятностей.
Определенный интеграл с переменным верхним пределом
(16)
называют функцией Лапласа. Для неё справедливы следующие равенства
. (17)
Функция Лапласа используется для определения значений интегральных функций нормальных распределений. Функция 
связана с функцией Лапласа формулой
. (18)
Поскольку интеграл в (16) не выражается через элементарные функции, то значения функции Лапласа для различных значений t сведены в таблицу.