Элементы комбинаторики
Формулы комбинаторики позволяют посчитать число способов проделать действие или число его возможных результатов.
Основной принцип комбинаторики заключается в следующем: если первый элемент можно выбрать  способами, а второй элемент -
способами, а второй элемент -  способами, то упорядоченную пару элементов можно составить
способами, то упорядоченную пару элементов можно составить  способами.
способами.
Урновые схемы. Есть урна (ящик), содержащая  пронумерованных шаров. Мы выбираем из урны
пронумерованных шаров. Мы выбираем из урны  шаров; результат этого выбора - набор из
шаров; результат этого выбора - набор из  шаров. Нас интересует, сколькими способами можно выбрать
шаров. Нас интересует, сколькими способами можно выбрать  шаров из
шаров из  , т. е. сколько различных результатов возможно.
, т. е. сколько различных результатов возможно.
Условимся, какие результаты выбора (какие наборы номеров шаров) мы будем считать различными. Есть ровно две возможности.
- Выбор с учетом порядка: два набора номеров шаров считаются различными, если они отличаются составом или порядком номеров. Так, наборы

 и
и  считаются различными наборами.
считаются различными наборами. - Выбор без учета порядка: два набора номеров шаров считаются различными, если они отличаются составом. Так, наборы
 и
и  различны, а наборы
различны, а наборы  и
и  не различаются.
не различаются.
Подсчитаем, сколько возможно различных результатов для каждой из схем выбора: с учетом порядка или без учета.
Выбор без возвращения и с учетом порядка
Общее количество различных наборов при выборе  элементов из
элементов из  без возвращения и с учетом порядка равняется
без возвращения и с учетом порядка равняется

Число  называется числом размещений из
называется числом размещений из  элементов по
элементов по  элементов, а сами результаты выбора - размещениями.
элементов, а сами результаты выбора - размещениями.
В множестве из  элементов возможно ровно Pn=
элементов возможно ровно Pn= 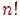 перестановок этих элементов.
перестановок этих элементов.
Выбор без возвращения и без учета порядка
Общее количество различных наборов при выборе  элементов из
элементов из  без возвращения и без учета порядка равняется
без возвращения и без учета порядка равняется

Число  называется числом сочетаний из
называется числом сочетаний из  элементов по
элементов по  элементов, а сами результаты выбора - сочетаниями.
элементов, а сами результаты выбора - сочетаниями.
События и операции над ними
Пространство элементарных исходов. Основным понятием теории вероятностей является множество всех возможных результатов данного случайного эксперимента.
Определение 1. Пространством элементарных исходов называется множество  (омега), содержащее все возможные взаимоисключающие результаты данного случайного эксперимента. Элементы множества
(омега), содержащее все возможные взаимоисключающие результаты данного случайного эксперимента. Элементы множества  называются элементарными исходами и обозначаются буквой
называются элементарными исходами и обозначаются буквой  .
.
Отметим сразу, что любое непустое множество  можно считать пространством элементарных исходов какого-то случайного эксперимента.
можно считать пространством элементарных исходов какого-то случайного эксперимента.
Определение 2. Событиями называются подмножества множества 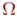 . Говорят, что произошло событие
. Говорят, что произошло событие 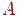 , если эксперимент завершился одним из элементарных исходов, входящим в множество
, если эксперимент завершился одним из элементарных исходов, входящим в множество  .
.
Итак, элементарный исход - это мельчайший неделимый результат эксперимента, а событие может состоять из одного или нескольких исходов.
Пример 1. Один раз подбрасывают игральную кость. Рассмотрим пространство элементарных исходов


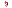

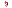

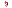

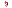

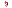


Элементарные исходы здесь соответствуют числу выпавших очков.
Событие 

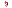

 произойдет, если выпадет одно или два очка; событие
произойдет, если выпадет одно или два очка; событие 

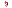

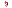

 означает, что выпадет нечетное число очков. Событие
означает, что выпадет нечетное число очков. Событие 

 состоит из одного элементарного исхода и означает появление шести очков.
состоит из одного элементарного исхода и означает появление шести очков.
Операции над событиями. В теории вероятностей рассматривают те же операции над событиями (множествами), что и в теории множеств. Дадим определения новым событиям - результатам этих операций.
Объединением  событий
событий 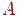 и
и  называется событие, состоящее в том, что из двух событий
называется событие, состоящее в том, что из двух событий 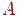 и
и  случилось хотя бы одно. Это событие включает как элементарные исходы из множества
случилось хотя бы одно. Это событие включает как элементарные исходы из множества  так и элементарные исходы из множества
так и элементарные исходы из множества  (рис. 1.1).
(рис. 1.1).
Пересечением  событий
событий 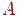 и
и  называется событие, состоящее в том, что произошли сразу оба события
называется событие, состоящее в том, что произошли сразу оба события 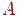 и
и  , Это событие содержит элементарные исходы, каждый из которых принадлежит и множеству
, Это событие содержит элементарные исходы, каждый из которых принадлежит и множеству  и множеству
и множеству  Вместо
Вместо  часто пишут просто
часто пишут просто 

Рис. 1.1. Объединение и пересечение событий
Дополнением  события
события  до
до 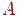 называется событие, состоящее в том, что произошло
называется событие, состоящее в том, что произошло 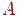 , но не произошло
, но не произошло  . Событие
. Событие  содержит элементарные исходы, входящие в множество
содержит элементарные исходы, входящие в множество 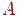 , но не входящие в
, но не входящие в  .
.
Противоположным (или дополнительным) к событию 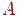 называется событие
называется событие  , состоящее в том, что
, состоящее в том, что 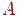 не произошло. Событие
не произошло. Событие 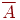 состоит из элементарных исходов, не входящих в множество
состоит из элементарных исходов, не входящих в множество 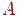 (рис. 1.2).
(рис. 1.2).

Рис. 1.2. Дополнение и противоположное событие
Выделим среди подмножеств  два особых события.
два особых события.
Достоверным называется событие, которое обязательно происходит в результате эксперимента, т. е. единственное событие, включающее все элементарные исходы - событие 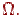
Невозможным называется событие, которое не может произойти в результате эксперимента, т. е. событие, не содержащее ни одного элементарного исхода - "пустое множество" 
Объединение множеств аналогично сложению чисел, пересечение - умножению:

Первое из этих равенств очевидно, а второе, хоть и противоречит интуиции, все же верно.
Пример 2. Пусть событие  означает, что
означает, что  -я деталь бракованная, где
-я деталь бракованная, где  - номер детали. Запишем с помощью операций над событиями событие
- номер детали. Запишем с помощью операций над событиями событие 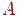 - "ровно две из трех деталей бракованные":
- "ровно две из трех деталей бракованные":

Выше записано буквально следующее: либо первые две детали бракованные, а третья годная, либо первая и третья детали бракованные, а вторая годная, либо вторая и третья детали бракованные, а первая годная.
Событие 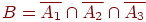 , означает "все три детали годные".
, означает "все три детали годные".
Событие "хотя бы одна деталь из трех бракованная" можно записать так  .
.
Отношения между событиями. Множества могут пересекаться или не пересекаться, быть включены одно в другое или не быть. В теории вероятностей эти отношения событий носят особые названия.
События 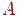 и
и  называются несовместными, если они не могут произойти одновременно:
называются несовместными, если они не могут произойти одновременно: 
События  называются попарно несовместными, если несовместны любые два из них, т. е.
называются попарно несовместными, если несовместны любые два из них, т. е.  для любых
для любых 
Говорят, что событие 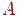 влечет событие
влечет событие  и пишут
и пишут  если всегда, как только происходит событие
если всегда, как только происходит событие  происходит и событие
происходит и событие  Это означает, что любой элементарный исход, входящий в множество
Это означает, что любой элементарный исход, входящий в множество  одновременно входит в множество
одновременно входит в множество  т. е.
т. е. 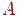 содержится в
содержится в  (рис. 1.3)
(рис. 1.3)

Рис. 1.3. Попарно несовместные и вложенные события
Пример 3. При бросании двух игральных костей события "сумма очков равна четырем" и "на первой кости выпало шесть очков" несовместны: они не могут случиться одновременно.
Событие "сумма очков равна двум" влечет за собой событие "на костях выпало одинаковое число очков". Действительно, сумма очков равна двум лишь при выпадении двух единиц. Но тогда на костях выпадет одинаковое число очков. Обратное включение неверно: не всегда, когда на костях выпадает одинаковое число очков, сумма этих очков равна двум.
Событие "сумма очков меньше пяти" влечет за собой событие "сумма очков меньше семи".