Вариант № 7692038
1. Найдите значение выражения 
Решение.
Найдём значение выражения:
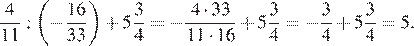
Ответ: 5.
2. Найдите значение выражения 
.
Решение.
Выполним преобразования:
.
Ответ: 5.
3. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 10 000 рублей?
Решение.
Розничная цена учебника составляет 120% от оптовой цены. Чтобы найти 100% цены разделим 180 на 1,2:
.
Поскольку
,
по оптовой цене на 10 000 рублей можно купить 66 учебников.
Ответ: 66.
4. Площадь любого выпуклого четырехугольника можно вычислять по формуле 
, где 
— длины его диагоналей, а 
угол между ними. Вычислите 
, если 
.
Решение.
Выразим 
:
Подставляя, получаем:
Ответ: 0,4.
5. Найдите значение выражения 
Решение.
Найдём значение выражения:
Ответ: 4.
6. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
Решение.
Расход воды составил 114 − 103 = 11 куб. м. Поэтому Алексей должен заплатить 11 · 19,2 = 211,2 руб.
Ответ: 211,2.
7. Решите уравнение: 
. Если уравнение имеет больше одного корня, в ответ укажите больший их них.
Решение.
Запишем уравнение в виде 
и подберем корни, пользуясь теоремой, обратной теореме Виета: получим числа −1 и 5. Больший из них равен 5.
8. 
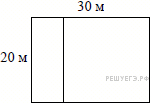Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
Решение.
Длина забора равна сумме периметра и ширины. Найдем периметр участка 30+30+20+20=100 м.
Длина забора 100+20=120 м.
Ответ: 120.
9. Установите соответствие между величинами и их возможными значениями:
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ | |
| А) скорость движения автомобиля Б) скорость движения пешехода В) скорость движения улитки Г) скорость звука в воздушной среде | 1) 0,5 м/мин 2) 60 км/час 3) 330 м/сек 4) 4 км/час |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
Упорядочим от медленного к быстрому. Ясно, что улитка самая медленная, человек быстрее улитки, автомобиль еще быстрее, а скорость звука — наибольшая из скоростей в списке. Получим соответствие В — 1, Б — 4, А — 2 и Г — 3.
Ответ: 2413.
10. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение.
Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·(1 − 0,9) = 0,04 и 0,6·(1 − 0,2) = 0,48. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,48 = 0,52.
Ответ: 0,52.
Приведем другое решение.
Джон попадает в муху, если схватит пристрелянный револьвер и попадет из него, или если схватит непристрелянный револьвер и попадает из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,4·0,9 = 0,36 и 0,6·0,2 = 0,12. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,36 + 0,12 = 0,48. Событие, состоящее в том, что Джон промахнется, противоположное. Его вероятность равна 1 − 0,48 = 0,52.
11. 
Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?
Решение.
Из графика видно, что при скорости 200 км в час действующая на крылья подъемная сила равна одной тонне силы.
Ответ: 1.
12. Телефонная компания предоставляет на выбор три тарифных плана.
| Тарифный план | Абонентская плата | Плата за 1 минуту разговора |
| Повременный | 135 руб. в месяц | 0,3 руб. |
| Комбинированный | 255 руб. за 450 мин. в месяц | 0,28 руб. за 1 мин. сверх 450 мин. в месяц |
| Безлимитный | 380 руб. в месяц |
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна 650 минут? Ответ дайте в рублях.
Решение.
Рассмотрим три случая.
На тарифном плане «Повременный» ежемесячная плата будет складываться из абонентской 135 руб. и платы за 650 мин. 650 
0,3 = 195 руб. и будет составлять 195 + 135 = 330 руб.
На тарифном плане «Комбинированный» ежемесячная плата будет складываться из абонентской 255 руб. и платы за 200 мин. сверх тарифа 200 0,28 = 56 руб. и будет составлять 255 + 56 = 311 руб.
На тарифном плане «Безлимитный» ежемесячная плата будет равна 380 рублям.
Стоимость самого дешевого варианта составляет 311 рублей.
Ответ: 311.
13. 
Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Решение.
Поверхности креста составлена из шести поверхностей кубов, у каждого из которых отсутствует одна грань. Тем самым, поверхность креста состоит из 30 единичных квадратов, поэтому ее площадь равна 30.
Ответ: 30.
14. На графике изображена зависимость скорости движения легкового автомобиля на пути между двумя городами от времени. На вертикальной оси отмечена скорость в км/ч, на горизонтальной — время в часах, прошедшее с начала движения автомобиля.
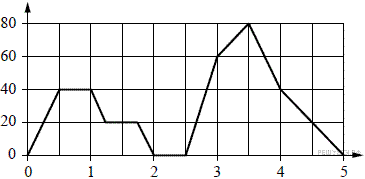
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автомобиля на этом интервале.
| ИНТЕРВАЛЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ | |
| А) второй час пути Б) третий час пути В) четвёртый час пути Г) пятый час пути | 1) автомобиль не разгонялся и некоторое время ехал с постоянной скоростью 2) скорость автомобиля постоянно снижалась 3) автомобиль сделал остановку 4) скорость автомобиля достигла максимума за всё время движения |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
На протяжении второго часа автомобиль не разгонялся и некоторое время ехал с постоянной скоростью.
На протяжении третьего часа пути автомобиль остановился на 30 мин., а затем продолжил движение.
На протяжении четвертого часа пути автомобиль набрал максимальную скорость 80 км/ч.
На протяжении пятого часа пути скорость автомобиля снижалась с 40 км/ч до нуля.
Таким образом, получаем соответствие: А — 1, Б — 3, В — 4 и Г — 2.
Ответ: 1342.
15. 
В прямоугольной трапеции 
с основаниями 
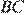и 
угол 
прямой,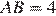 
, 
. Найдите среднюю линию трапеции.
Решение.
Для того, чтобы найти среднюю линию трапеции необходимо знать длину оснований, найдём AD.
Проведём высоту СH к AD.
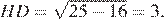
Найдём АD:
Средняя линия трапеции равна полусумме оснований:
Ответ: 6,5.
16. 
Объём конуса равен 50 π, а его высота равна 6. Найдите радиус основания конуса.
Решение.
Объём конуса вычисляется по формуле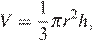 
откуда, 
Ответ: 5.
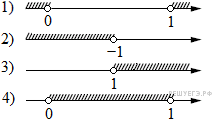
17. Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
| НЕРАВЕНСТВА | РЕШЕНИЯ | |
А)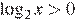 
Б) 
В) 
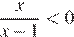Г) 
| 
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| А | Б | В | Г |
Решение.
Решим неравенства:
А)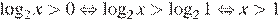 
Б)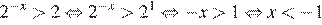 
В)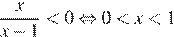 
Г) 
Ответ: 3241.
18. Известно, что спектр ртутной лампы — линейчатый. Выберите утверждения, которые следуют из этого факта.
1) У любой ртутной лампы линейчатый спектр.
2) Любая лампа с линейчатым спектром — ртутная.
3) У любой нертутной лампы спектр не является линейчатым.
4) Если спектр лампы линейчатый то она может быть ртутной.
Решение.
1) Верно.
2) У всех ртутных ламп линейчатый спектр. Про спектр всех остальных ламп ничего не известно. У некоторых из них может быть и линейчатый.
3) В прошлом пункте уже было сказано, что про спектр нертутных ламп ничего не сказано.
4) Так как у всех ртутных ламп линейчатый спектр, то среди ламп с линейчатым спектром определённо есть ртутные лампы.
Ответ: 14.
19. Найти четырехзначное число, кратное 44, любые две соседние цифры которого отличаются на 1. В ответе укажите любое такое число.
Решение.
Если число делится на 44, то оно делится на 4 и на 11. Так как число делится на 4 и две последние цифры должны отличаться на 1, число должно заканчиваться на 12, 32, 56, 76.
Пусть число имеет вид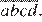 
Число делится на 11, если модуль разности сумм цифр, стоящих на чётных и нечётных местах, делится на 11. В нашем случае, если 
делится 11.
Но модуль 
равен 1, модуль 
равен 1, а значит 
принимает значения 
Из них делится на 11 только число 0. Значит,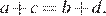 
Необходимо подобрать такие комбинации цифр, чтобы сумма цифр чётных разрядов была равна сумме цифр нечётных разрядов, и при этом эти цифры не должны отличаться друг от друга более, чем на 1.
Такими числами являются 1012, или 3432, или 5456, или 3212, или 1232, или 5676, или 7876, или 7656.
Ответ: 1012, или 3432, или 5456, или 3212, или 1232, или 5676, или 7876, или 7656.
Примечание.
Условие «любые две соседние цифры отличаются на 1» означает, что каждые две соседние цифры должны отличаться на 1.
20. Про натуральные числа A, B и С известно, что каждое из них больше 6, но меньше 10. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 186. Какое число было загадано?
Решение.
Числа А, В и С могут быть равны 7, 8 или 9.
Пусть загадали натуральное число Х, тогда Х · А + В – С = 186 или Х · А = 186 + (С – В). Рассмотрим различные случаи.
1) С – В = 0 (7 – 7 = 0, 8 – 8 = 0 или 9 – 9 = 0), тогда Х · А = 186. Число 186 не делится нацело на 7, на 8 и на 9, значит, этот случай не подходит.
2) С – В = 1 (8 – 7 = 1 или 9 – 8 = 1), тогда Х · А = 187. Число 187 не делится нацело на 7, на 8 и на 9, значит, этот случай не подходит.
3) С – В = –1 (7 – 8 = –1 или 8 – 9 = –1), тогда Х · А = 185. Число 185 не делится нацело на 7, на 8 и на 9, значит, этот случай не подходит.
4) С – В = 2 (9 – 7 = 2), тогда Х · А = 188. Число 188 не делится нацело на 7, на 8 и на 9, значит, этот случай не подходит.
5) С – В = –2 (7 – 9 = –2), тогда Х · А = 184. Число 184 делится нацело на A = 8, значит, Х = 23.
Ответ: 23.
Вариант № 25976461
1. Поезд Казань-Москва отправляется в 21:35, а прибывает в 10:35 на следующий день (время московское). Сколько часов поезд находится в пути?
Решение.
В день отправления поезд едет (24 − 21) · 60 − 35 = 3 · 60 − 35 = 145 минут, а на следующий день до момента прибытия он едет 10 · 60 + 35 = 635 минут. Всего в пути поезд проведет 145 + 635 = 780 минут. Разделим 780 на 60:
Значит, поезд находится в пути 13 часов.
Ответ: 13.
Примечание.
Через 12 часов от момента отправления поезда будет 9:35, значит, поезд идет 13 часов.
2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.
Решение.
Из 16 наблюдений, представленных на графике, 2 дня выпадало более 3 мм осадков в остальные дни менее 3 мм осадков. Поэтому 14 дней выпадало менее 3 мм осадков.
Ответ: 14.
3. 
На клетчатой бумаге с размером клетки 
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Решение.
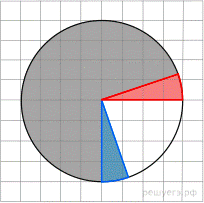Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого 
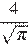см. Поэтому
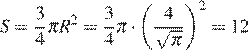см2.
Ответ: 12.
4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
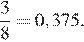
Ответ: 0,375.
5. Решите уравнение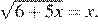 
Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Решение.
Возведем в квадрат:
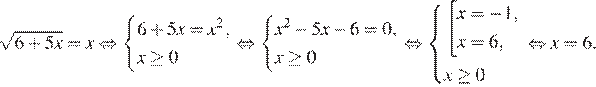
Уравнение имеет единственный корень, он и является ответом.
Ответ: 6.
Примечание.
Можно было сделать проверку. Подставляя число 6, получаем верное равенство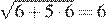 
, поэтому число 6 является корнем. Подставляя число −1, получаем неверное равенство 
, поэтому число −1 не является корнем.
6. 
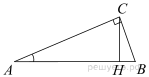В треугольнике ABC угол C равен 90°, 
, 
Найдите высоту CH.
Решение.
Поскольку 
, 
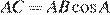имеем:
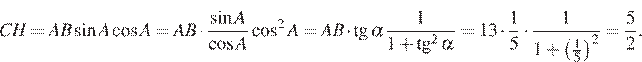
Ответ: 2,5.