Пусть длина катета ВС равна х, тогда длина АС равна 5 х, а длина гипотенузы равна 
Зная, что гипотенуза равна 13, находим: 
Поскольку проведенная к гипотенузе высота равна произведению катетов, деленному на гипотенузу, имеем:
7. На рисунке изображён график некоторой функции 
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F (8) − F (2), где F (x) — одна из первообразных функции f (x).
Решение.
Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции 
Поэтому
Ответ:7.
8. 
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.
Решение.
Площадь поверхности куба выражается через его ребро 
формулой 
, поэтому при увеличении длины ребра на 
площадь увеличится на
Отсюда находим, что ребро куба равно
Ответ: 4.
9. Найдите значение выражения 
Решение.
Выполним преобразования:
Ответ: 1.
10. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время 
падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле 
, где 
– расстояние в метрах, 
– время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Решение.
Пусть 
– расстояние до воды до дождя, 
– расстояние до воды после дождя. После дождя уровень воды в колодце повысится, расстояние до воды уменьшится, и время падения уменьшится, станет равным 
с. Уровень воды поднимется на 
метров.
Ответ: 1.
11. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
Решение.
Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 21 км/ч. Пусть первый раз мотоциклисты поравняются через 
часов. Для того, чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому
Таким образом, мотоциклисты поравняются через 
часа или через 20 минут.
Ответ: 20.
Приведём другое решение.
Быстрый мотоциклист движется относительно медленного со скоростью 21 км в час, и должен преодолеть разделяющие их 7 км. Следовательно, на это ему потребуется одна треть часа.
12. Найдите наибольшее значение функции 
на отрезке 
Решение.
Найдем производную заданной функции:
Найдем нули производной на заданном отрезке:
Определим знаки производной функции на заданном отрезке и изобразим на рисунке поведение функции:
В точке 
заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение:
Ответ: 12.
13. а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку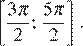 
Решение.
а) 
б) С помощью числовой окружности отберём корни, принадлежащие отрезку 
Получим число 
Ответ: а) 
б) 
14. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 9.
Основание O высоты SO этой пирамиды является серединой отрезка SS 1, M — середина ребра SB, точка L лежит на ребре CD так, что CL: LD = 7: 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S 1 LM — равнобедренная трапеция.
б) Вычислите длину средней линии этой трапеции.
Решение.
а) Проведём медиану S 1 M треугольника SS 1 B, которая пересекает прямую BB 1, являющуюся одновременно медианой треугольника SS1B и основания BCD, в точке T. Тогда ВТ: ТВ 1 = 4: 5.
Точка L, в свою очередь, делит отрезок B 1 D в отношении DL: LВ 1 = 4: 5, так как LD: LC = 2: 7 и отрезок BB 1 — медиана треугольника BCD.
Следовательно, сторона сечения, проходящая через точки L и T, параллельна стороне BD основания BCD. Пусть прямая LT пересекает BC в точке P.
Проведём через точку M среднюю линию в треугольнике SBD, пусть она пересекает сторону SD в точке K. Тогда PMKL — искомое сечение, причём BP = DL и BM = KD. Из равенства треугольников BMP и DKL получим MP = KL, а значит, PMKL — равнобедренная трапеция.
б) Большее основание PL трапеции равно 7, поскольку треугольник LPC правильный. Второе основание MK равно 4,5, поскольку MK — средняя линия правильного треугольника SBD. Следовательно, средняя линия трапеции равна 
Ответ: 5,75.
15. Решите неравенство 
Решение.
Перепишем неравенство в виде 
и положим 
Тогда 
и, значит, 
Далее имеем: 
откуда 
Ответ: 
16. Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8 MB и DN = 2 CN.
а) Докажите, что AD = 4 BC.
б) Найдите длину отрезка MN, если радиус окружности равен 
Решение.
а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.
Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому
то есть треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8 x, DN = 2 y.
откуда y = 2 x. Получаем: BK = BM = x, AL = AM = 8 x, CK = CN = 2 x, DL = DN = 4 x, BC = BK + KC = 3 x, AD = AL + LD = 12 x, то есть AD = 4 BC.
б) Заметим, что 
поэтому 
Пусть прямые AB и CD пересекаются в точке P, а прямые MN и PO пересекаются в точке Q. Тогда треугольники BPC и APD подобны, поэтому AP = 4 BP, AB = 3 BP, BP = 3 x, PN = PM = 4 x. Прямая PO является серединным перпендикуляром к MN. В прямоугольном треугольнике OMP получаем:
Значит, 
Ответ: б) 4.