Приведем другое решение пункта а)

Пусть окружность касается оснований BC и AD в точках K и L соответственно, ее центр находится в точке O, а BM = x, CN = y, тогда AM = 8 x, DN = 2 y. Поскольку точки M, K, N и L — точки касания, 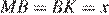, , и Опустим высоты BH и CQ:

тогда по теореме Пифагора Поскольку имеем откуда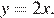

Таким образом, BC = BK + KC = 3 x, AD = AL + LD = 12 x, то есть AD = 4 BC.

17. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

− каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.

Если ежегодно выплачивать по 58 564 рублей, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рублей, то кредит будет полностью погашен за 2 года. Найдите r.

Решение.

Пусть сумма кредита S ежегодные выплаты x, По условию долг на июль меняется так:

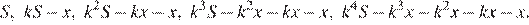
Если долг выплачен двумя равными платежами x ₂, то откуда

Если долг выплачен четырьмя равными платежами x ₄, то 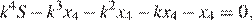откуда

Тогда

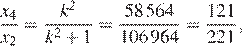
откуда Следовательно,

Ответ: 10.

18. Найти все значения параметра при каждом из которых среди значений функции 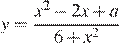есть ровно одно целое число.

Решение.

Функция определена и непрерывна на всей числовой прямой. Уравнение 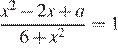при любом имеет решение Значит, при любом одно из значений функции равно 1.

Поскольку функция непрерывна, множество её значений образует промежуток, включающий число 1. Других целых значений функции нет, если для всех

Чтобы неравенства выполнялись для всех дискриминанты обоих трёхчленов должны быть отрицательны:

Таким образом, подходящие значения параметра

Ответ: (1; 11).

19. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.

а) Мог ли средний балл в школе № 1 вырасти в два раза?

б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный балл в школе № 2 равняться 1?

в) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.

Решение.

а) Пусть в школе № 1 писали тест n учащихся, а средний балл был равен А. Тогда суммарный балл всех учащихся этой школы равнялся nA, а значит, после перехода одного учащегося в школу № 2, суммарный балл стал равен Таким образом, суммарный балл уменьшился на что невозможно, поскольку перешедший учащийся набрал положительное количество баллов, а

б) Пусть в школе № 2 средний балл равнялся В, а перешедший в нее учащийся набрал u баллов. Тогда получаем:

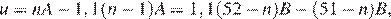
или

Если то поскольку число должно делиться на 10, а не должно быть отрицательным. Получаем что невозможно, поскольку A целое.

в) Заметим, что если то или В первом случае а во втором Значит, ни один из этих случае не возможен.

При получаем 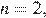откуда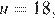 Этот случай реализуется, например, если в школе № 1 писали тест 2 учащихся и набрали 22 и 18 баллов, а в школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.

Ответ: а) нет; б) нет; в) 3.