События Виды событий
Цель: ввести понятие события; знакомство с различными видами событий; и операций над ними 1.
События.
Все, что происходит или не происходит в реальной действительности, называют явлениями или событиями. Если некоторое событие происходит довольно часто, то в его наступлении существует определенная закономерность. Раздел математики, изучающий закономерности массовых явлений называется теорией вероятностей.
2. Виды событий.
1) Событие, которое в некотором испытании может произойти, а может и не произойти, называют случайным событием.
2) Событие, которое в данном испытании обязательно произойдет, называют достоверным событием.
3) Событие, которое в данном испытании наступить не может, называют невозможным событием.
Играющий бросает кубик и смотрит, какое число выпало на грани, которая располагается сверху. Какие предположения он может сделать, когда бросает игральный кубик? Например, такие:
событие А – выпадет цифра 1, 2, 3, 4, 5 или 6 – достоверное;
событие В – выпадет цифра 7, 8 или 9 – невозможное;
событие С – выпадет цифра 1– случайное.
4) События несовместны, если появление одного из них исключает появление другого.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, – несовместимыми.
5) События называются равновозможными, когда в их испытании нет преимуществ.
Действия над событиями.
Суммой ( объединением 
двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из данных событий.
Произведением (пересечением событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В.
|
|
Разностью А\В событий А и В называется событие, состоящее в том, что произойдет та часть события А, которая не входит в В.
Например. Пусть в опыте с бросанием игральной кости события: А – выпало число очков, кратное 2; В – выпало число очков, кратное 3. Тогда событие А + В означает, что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ – выпало число 6.
Событие противоположное к данному. А или дополнение события А.
Задача. Пусть из колоды вынимают одну карту. Рассмотрим события:
А – это король, В – это карта масти пик.
Тогда: А + В – вынут король или карта масти пик;
АВ – из колоды вынут король пик.
Для каждого события А можно рассмотреть противоположное событие Ā, которое наступит тогда и только тогда, когда событие А не наступает.
Например: А – выпадение чётного числа очков, Ā – выпадение нечетного числа очков; А – попадание в цель, Ā – промах.
Теорема: Если события А и В несовместны, то их произведение есть невозможное событие.
Полной группой событий называется совокупность всех возможных результатов опыта обозначают Ω
1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произойдет либо событие А, либо событие В, либо, если это возможно, они произойдут одновременно.
2. Произведением А*В событий А и В называется событие, состоящее в том, что события А и В произойдут одновременно.
Пусть определенное испытание проводится многократно в одних и тех же условиях и при этом каждый раз фиксируется, произошло интересующее нас событие А или нет. Обозначим буквой n общее число испытаний, а буквой m число испытаний, при которых произошло событие А. Число m называют частотой события А, а отношение m/ n – относительной частотой. P*(A) - относительная частота (частота).
|
|
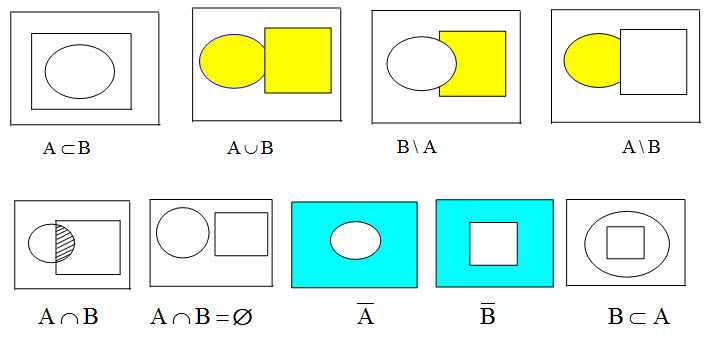
Геометрическая интерпретация операций над событиями
Пусть событие A - { выбрали случайные точки, они попали в круг }
, B - { точки попали в квадрат }
На первом рисунке А является подмножеством В
