Глава 2. Определители 2-го и 3-го порядков.
В настоящей главе вводится понятие определитель. Учитывая, что аудитория, для которой предназначено настоящее пособие – студенты технических специальностей, изучение определителей начнём с конкретных задач: решение простейших систем линейных уравнений.
Учтём, что, в отличие от школьника, студент должен знать, что математика есть инструмент моделирования различных технических процессов, в которых исходно участвуют параметры-буквы, а не числа. Изменяя эти параметры, инженер старается найти наиболее эффективные условия реализации процесса. Именно поэтому, нас интересует такое решение, запись которого содержит исходные параметры процесса, то есть коэффициенты систем уравнений (аналитических моделей)! Так если процесс описан системой уравнений:
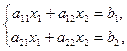 (1)
(1)
то нужно искать такую форму записи решения, в которую войдут все коэффициенты заданной системы уравнений.
Определители второго порядка.
Пусть задана система 2-х уравнений с двумя неизвестными (1). Известно, что при решении любой системы уравнений необходимо добиться разделения переменных, то есть получить уравнения, в каждое из которых входит только одна неизвестная величина!
Для получения уравнения, содержащего только неизвестную x 1, применим к системе уравнений (1) последовательные действия:
▫ умножим 1-е уравнение на число a 22;
▫ умножим 2-е уравнение на число –a 12;
▫ сложим получившиеся уравнения:
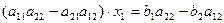 , или
, или 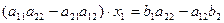 . (2)
. (2)
Для получения уравнения, содержащего только неизвестную x 2, применим к системе уравнений (1) действия:
▫ умножим 1-е уравнение на число a 21;
▫ умножим 2-е уравнение на число –a 11;
▫ сложим получившиеся уравнения:
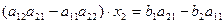 , или
, или 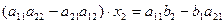 . (3)
. (3)
Для облегчения запоминания выражений (2) и (3) придумали специальную конструкцию, такую, что реализуется соответствие:
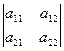 =
= 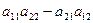 . (4)
. (4)
Левую часть выражения (4) назвали определителем 2-го порядка, правая часть выражает правило его вычисления. При использовании определителя применяют термины:
▫ элементы определителя – числа a 11, a 12, a 21, a 22;
▫ строки определителя: 1-я строка: пара чисел: a 11, a 12, 2-я строка: пара чисел a 21, a 22;
▫ столбцы определителя: 1-й столбец: пара чисел: a 11, a 21, 2-й столбец: пара чисел a 12, a 22;
▫ члены определителя: (a 11· a 22) и (– a 21· a 12).
При внимательном рассмотрении соответствия (4) нетрудно заметить правило использования элементов определителя для записи суммы левой части выражения (4). Для записи положительного члена определителя (a 11· a 22) используют схему:

Для записи отрицательного члена определителя (– a 21· a 12) используют схему:

Воспользуемся понятием матрицы, для формального определения определителя 2-го порядка:
квадратная матрица: A = 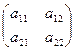 → определитель:
→ определитель: 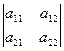 =| A |= d.
=| A |= d.
Учитывая соответствие (4), правые части выражений (2) и (3) можем записать в виде:
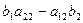 =
= 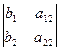 = d 1,
= d 1, 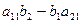 =
= 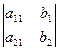 = d 2, (5)
= d 2, (5)
после чего получаем компактные записи выражений (2) и (3):
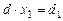 ,
, 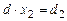 . (6)
. (6)
Если проследить переход от записи системы уравнений (1) до записи выражений (6), нетрудно заметить, что это всегда выполнимо! Далее необходимо совершить ещё один шаг (последний!): записать выражения для вычисления неизвестных x 1 и x 2. Но этот шаг не всегда выполним, так как связан с делением на число d, которое может быть равно нулю.
Если d =0, то 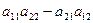 =0, откуда следует:
=0, откуда следует: 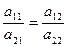 , то есть пропорциональность строк определителя.
, то есть пропорциональность строк определителя.
1*. Пусть d ≠0. В этом случае решение системы (3) может быть записано при помощи формул Крамера (используются выражения (6)): 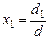 ,
, 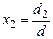 . (7)
. (7)
Формулы (7) определяют единственное решение (т.к. отношение двух чисел, принадлежащих полю вещественных чисел, определяет единственное число!).
2*. Пусть d =0. В этом случае выразить x1 и x2 из (6) не удаётся: деление на нуль не определено в поле вещественных чисел. Как отмечалось, из условия d =0 следует: строки матрицы A пропорциональны: 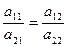 =
= 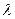 . Чем может закончиться решение системы уравнений в этом случае? Возможны два исхода:
. Чем может закончиться решение системы уравнений в этом случае? Возможны два исхода:
1) Если выполняется условие: 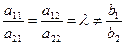 → d1 ≠ 0 и d2 ≠ 0. Но в этом случае равенства (6) невозможны! Это значит, что система (1) не имеет решения; в этом случае говорят – система несовместна.
→ d1 ≠ 0 и d2 ≠ 0. Но в этом случае равенства (6) невозможны! Это значит, что система (1) не имеет решения; в этом случае говорят – система несовместна.
2) Если выполняется условие: 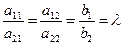 → d1 = 0 и d2 = 0 (причем одновременно!). В этом случае равенства (6) выполняются при любых значениях неизвестных x 1 и x 2. Можно заметить, что в этом случае 1-е уравнение можно получить, умножив 2-е уравнение на число
→ d1 = 0 и d2 = 0 (причем одновременно!). В этом случае равенства (6) выполняются при любых значениях неизвестных x 1 и x 2. Можно заметить, что в этом случае 1-е уравнение можно получить, умножив 2-е уравнение на число 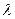 . Это значит, что фактически система состоит из одного уравнения, и одной из переменных можно присваивать произвольные значения; в этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.
. Это значит, что фактически система состоит из одного уравнения, и одной из переменных можно присваивать произвольные значения; в этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.
Если вспомнить, что уравнение вида: 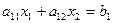 есть уравнение прямой, то геометрический смысл решения системы уравнений (1) состоит в нахождении точки пересечения двух прямых: l 1:
есть уравнение прямой, то геометрический смысл решения системы уравнений (1) состоит в нахождении точки пересечения двух прямых: l 1: 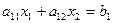 , l 2:
, l 2: 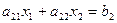 .
.
Для каждой прямой запишем соответствующий вектор нормали: 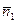 =(a 11, a 12) и
=(a 11, a 12) и  =(a 21, a 22) и рассмотрим возможные случаи их взаимного расположения:
=(a 21, a 22) и рассмотрим возможные случаи их взаимного расположения:
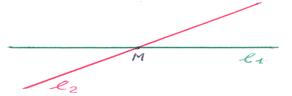 1*. Прямые l 1, l 2 пересекаются. Из геометрии следует, что точка пересечения единственна. В этом случае векторы
1*. Прямые l 1, l 2 пересекаются. Из геометрии следует, что точка пересечения единственна. В этом случае векторы  ,
,  не параллельны. Но, тогда их координаты: (a 11, a 12) и (a 21, a 22) не пропорциональны. Следовательно, все определители выражений (6) не равны нулю: d ≠0, d 1 ≠0, d 2 ≠0 и выражения (7) определяют единственное решение системы уравнений (1). Из этого следует: единственность решения системы уравнений (1) соответствует точке пересечения прямых, определяемых уравнениями системы.
не параллельны. Но, тогда их координаты: (a 11, a 12) и (a 21, a 22) не пропорциональны. Следовательно, все определители выражений (6) не равны нулю: d ≠0, d 1 ≠0, d 2 ≠0 и выражения (7) определяют единственное решение системы уравнений (1). Из этого следует: единственность решения системы уравнений (1) соответствует точке пересечения прямых, определяемых уравнениями системы.
 2*. Прямые l 1, l 2 параллельны и различны. Из геометрии следует, что точек пересечения у этих прямых нет. В этом случае для векторов
2*. Прямые l 1, l 2 параллельны и различны. Из геометрии следует, что точек пересечения у этих прямых нет. В этом случае для векторов 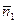 ,
, 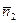 верно:
верно: 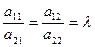 . Так как прямые l 1и l 2 различны, то:
. Так как прямые l 1и l 2 различны, то: 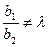 . Из свойств определителя 2-го порядка следует, что в этом случае: d =0, но d1 ≠0, d2 ≠0 → выражения (6) не выполняются ни при каких значениях x 1 и x 2. В этом случае система уравнений (1) не имеет решения, что соответствует аксиоме о параллельности прямых: точки пересечения нет.
. Из свойств определителя 2-го порядка следует, что в этом случае: d =0, но d1 ≠0, d2 ≠0 → выражения (6) не выполняются ни при каких значениях x 1 и x 2. В этом случае система уравнений (1) не имеет решения, что соответствует аксиоме о параллельности прямых: точки пересечения нет.
 3*. Прямые l 1, l 2 совпадают. Из геометрии следует, что любая точка прямой l 1 принадлежит и прямой l 2. В этом случае для векторов
3*. Прямые l 1, l 2 совпадают. Из геометрии следует, что любая точка прямой l 1 принадлежит и прямой l 2. В этом случае для векторов 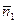 ,
, 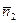 верно:
верно: 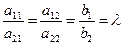 . Это значит, что система уравнений (1) эквивалентна одному уравнению и выполняется: d =0 и d1 =0, d2 =0 → выражения (6) выполняются при любых значениях x 1 и x 2: система уравнений (1) имеет бесчисленное множество решений, что совпадает с геометрическим решением!
. Это значит, что система уравнений (1) эквивалентна одному уравнению и выполняется: d =0 и d1 =0, d2 =0 → выражения (6) выполняются при любых значениях x 1 и x 2: система уравнений (1) имеет бесчисленное множество решений, что совпадает с геометрическим решением!
Если свободные члены системы b1, b2 равны одновременно нулю, то система (1) принимает вид:
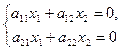 (8)
(8)
и имеет специальное название – однородная система уравнений. В этом случае каждое уравнение определяет прямую, проходящую через начало координат.
Система уравнений (8) всегда имеет решение (0,0), что подтверждается подстановкой пары чисел (0,0) в систему уравнений. Это же следует из того, что обе прямые l1 и l2 проходят через начало координат: (0,0). И в этом случае применение определителей позволяет получить соответствующие характеристики возможных случаев.
Если d ≠0, то прямые l1 и l2 пересекаются. Но в этом случае оба определителя d1 и d2 равны нулю: каждый из них имеет один из столбцов, содержащий только нули! Из выражений (6) и из формул Крамера следует: единственным решением системы (8) является точка (0,0) – точка пересечения прямых.
Если d =0, то прямые l1 и l2 совпадают → система имеет бесчисленное множество решений, так как выражения (6) выполняются при любых значениях x 1 и x 2.
☺☺
Пример 2 – 01: Вычислить определитель 2-го порядка: d = 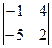 .
.
Решение:
1). Воспользуемся общей формулой: 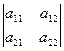 =
= 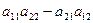 .
.
2). В нашем примере: d =(-1)·2–(-5)·4 = 18.
Ответ: d =18.
Пример 2 – 02: Вычислить определитель 2-го порядка: d = 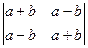 .
.
Решение:
1). Воспользуемся общей формулой: 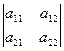 =
= 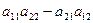 .
.
2). В нашем примере: d =(a + b)·(a + b)–(a – b)·(a – b) = 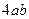 .
.
Ответ: d = 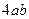 .
.
Пример 2 – 03: Вычислить определитель 2-го порядка: d = 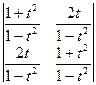 .
.
Решение:
1). Упростим запись определителя: d = 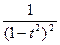 ·
· 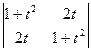 =
= 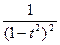 ·d 1: вынесением общего множителя
·d 1: вынесением общего множителя 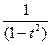 из 1-й и 2-й строк получили для вычисления значительно более простую форму – определитель d 1!
из 1-й и 2-й строк получили для вычисления значительно более простую форму – определитель d 1!
2). Вычислим: d 1 = 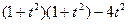 =
= 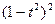 , тогда, очевидно, d =1.
, тогда, очевидно, d =1.
Ответ: d =1.
Пример 2 – 04: Вычислить определитель 2-го порядка: d = 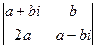 .
.
Решение:
1). Воспользуемся общей формулой: 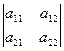 =
= 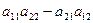 .
.
2). В нашем примере: d = 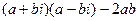 =
= 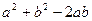 =
= 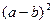 . Учтено:
. Учтено: 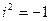 .
.
Ответ: d = 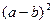 .
.
Пример 2 – 05: Вычислить определитель 2-го порядка: d = 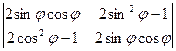 .
.
Решение:
1) Учтём: 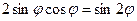 ,
, 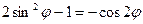 ,
, 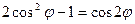 .
.
2) Воспользуемся общей формулой: 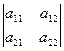 =
= 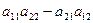 .
.
3) Для заданного определителя (с учётом выполненных тригонометрических преобразований) получаем: d = 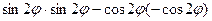 =1.
=1.
Ответ: d = 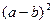 .
.
Пример 2 – 06: Доказать, что определитель 2-го порядка: d = 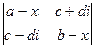 есть уравнение, у которого корни – действительные числа, если a, b, c, d – действительные числа.
есть уравнение, у которого корни – действительные числа, если a, b, c, d – действительные числа.
Решение:
1). Вычислим определитель: d = 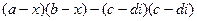 =
= 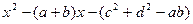 .
.
2). Запишем дискриминант полученного уравнения: D= 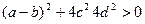 .
.
3). Условие действительности корней квадратного уравнения: D>0 – выполнено!
Ответ: 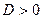 → корни – действительные числа.
→ корни – действительные числа.
Замечание: рассмотренные примеры иллюстрируют вычисление определителей 2-го порядка перед тем, как заняться их применением при решении систем линейных уравнений.
Пример 2 – 07: Решить систему уравнений: 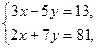 по правилу Крамера.
по правилу Крамера.
Решение:
1). Составим определитель системы: d = 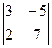 и определители:
и определители: 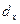 =
= 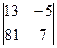 , заменяя 1-й столбец определителя d столбцом
, заменяя 1-й столбец определителя d столбцом 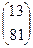 правой части;
правой части; 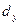 =
= 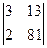 , заменяя 2-й столбец определителя d столбцом
, заменяя 2-й столбец определителя d столбцом 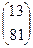 правой части.
правой части.
2). Вычислили: d =31, 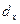 = 496,
= 496, 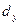 =217.
=217.
3). Применяя правило Крамера, получим: x = 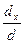 =
= 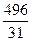 =16; y =
=16; y = 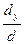 =
= 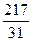 =7.
=7.
Ответ: x =16; y =7.
Пример 2 – 08: Решить уравнение: 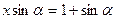 по правилу Крамера.
по правилу Крамера.
Решение:
1). Учтём, что линейное уравнение с одной неизвестной – это частный случай систем уравнений. Поэтому: d =  ,
, 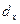 =
= 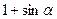 .
.
2). Тогда запишем: x = 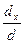 =
= 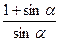 , которое верно при
, которое верно при  ≠0, то есть
≠0, то есть  ≠
≠ 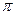
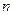 .
.
3). Если  =
= 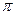
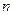 , то решений нет, так как равенство x · d =
, то решений нет, так как равенство x · d = 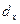 невозможно ни при каком x.
невозможно ни при каком x.
Ответ: уравнение имеет решение при условии  ≠
≠ 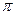
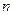 .
.
Пример 2 – 09: Исследовать систему уравнений: 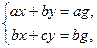 используя теоретические результаты, полученные в § 1.
используя теоретические результаты, полученные в § 1.
Решение:
1). Составим определитель системы: d = 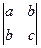 и определители:
и определители: 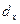 =
= 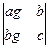 , заменяя 1-й столбец определителя d столбцом
, заменяя 1-й столбец определителя d столбцом 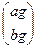 правой части;
правой части; 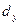 =
= 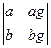 . заменяя 2-й столбец определителя d столбцом
. заменяя 2-й столбец определителя d столбцом 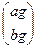 правой части.
правой части.
2). Вычислили: d = 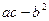 ,
, 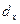 =
= 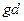 ,
, 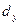 =0. Тогда, используя
=0. Тогда, используя 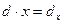 ,
, 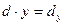 при d ≠ 0 получим: x =g, y =0; при d = 0: x, y – любые числа.
при d ≠ 0 получим: x =g, y =0; при d = 0: x, y – любые числа.
Ответ: при d ≠ 0 система уравнений единственное решение; при d = 0 их бесчисленное множество.
Пример 2 – 10: Имеем дробь: 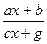 , причём хотя бы одно из чисел
, причём хотя бы одно из чисел 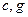 отлично от нуля. Показать, что значение дроби не зависит от значения x, если
отлично от нуля. Показать, что значение дроби не зависит от значения x, если  =0.
=0.
Решение:
1). Пусть при любом x имеем: 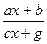 =q. Это значит:
=q. Это значит: 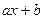 =
= 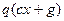 .
.
2). Известно, что равенство многочленов понимается как тождество. Поэтому должно быть: a = 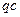 и b =
и b = 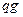 . Из условия также имеем:
. Из условия также имеем:  =
= 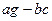 =0.
=0.
3). При 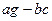 =0 рассмотрим все возможные ситуации по отношению к числам
=0 рассмотрим все возможные ситуации по отношению к числам 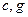 :
:
▫ с ≠ 0, g ≠0. Из 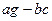 =0 можем записать:
=0 можем записать: 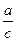 =
= 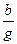 =q, откуда: a =
=q, откуда: a = 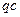 и b =
и b = 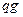 .
.
▫ с = 0, g ≠0. Теперь должно быть: a =0. Примем: 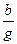 =q, после чего: a =
=q, после чего: a = 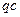 и b =
и b = 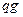 .
.
▫ с ≠ 0, g =0. Теперь должно быть: b =0. Примем: 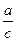 =q, после чего: a =
=q, после чего: a = 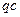 и b =
и b = 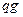 .
.
4). Итак, заданные условия обеспечивают независимость значения дроби от значений x.
Ответ: утверждение доказано.
☻