Определители третьего порядка.

Для определителей 3-го порядка можно было, как и для определителей 2-го порядка, начинать с системы 3-х уравнений с тремя неизвестными. Реализуя идею: разделить переменные так, чтобы в одно уравнение входила только одна неизвестная величина, мы обязательно придём к конструкции определитель 3-го порядка! Но, такой способ использовал бы такие неожиданные догадки, что естественность движения от практики к теории превратилась бы в свою противоположность!

И в то же время, мы договорились следовать от простого к сложному, используя принципы обобщений! Посмотрим ещё раз на правило записи определителя 2-го порядка:

квадратная матрица: A = 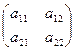→ определитель: = .

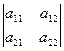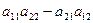Первое, что доступно для использования в обобщении: от определителя 2-го порядка к определителю 3-го порядка, записать соответствие:

квадратная матрица: A = 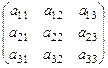→ определитель: 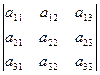=| A |= d,

которое есть копирование образа и не продвигает нас по пути обобщения никак!

Если внимательно посмотреть на правило построения суммы членов определителя 2-го порядка, то можно заметить:

1*. Член определителя: произведение двух его элементов, взятых по одному из каждой строки и каждого столбца. Число членов определителя: определяется перестановкой 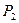=2!

2*. Знак члена определителя: со знаком 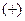мы берём произведение элементов определителя, расположенных на главной диагонали, а со знаком 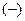: произведение элементов определителя, расположенных на побочной диагонали. 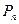= n!

Для того, чтобы определитель 3-го порядка сохранял выделенные свойства, необходимо потребовать:

1*. Член определителя: произведение трёх его элементов, взятых по одному из каждой строки и каждого столбца. Число членов определителя: определяется перестановкой 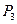=3!

2*. Знак члена определителя: со знаком 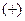мы берём произведение 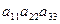– элементов определителя, расположенных на главной диагонали, со знаком 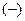: произведение 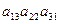– элементов определителя, расположенных на побочной диагонали...

А как определить знак члена определителя, использующего произведение 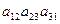? А все остальные?.. Соединим отрезками выделенные элементы: видим треугольник. А что случится с треугольником, если вершина a ₃₁ исчезнет? Останется отрезок 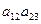, параллельный главной диагонали! Вот и разгадка! Произведение 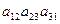нужно брать со знаком 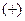, также и произведение 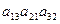. А со знаком 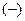нужно брать: 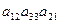и 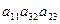. Так как перечислено шесть членов определителя, то ни один не забыт, ни одного лишнего: так как 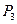=6!

Учитывая отмеченные свойства, для определителя 3-го порядка установим соответствие:

= + + – – – .

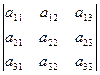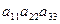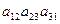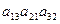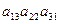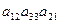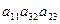Представленное соответствие, то есть формула для вычисления определителя, легко запоминается, если использовать геометрическую схему составления членов определителя:

Замечание: для того, чтобы применить определитель 3-го порядка к решению системы 3-х уравнений с тремя неизвестными, необходимо изучить свойства этого определителя по отношению к операции вычисление.

Свойство 1. Величина определителя не изменится, если строки и столбцы этого определителя поменять ролями, для матрицы это преобразование называется транспонированием:

d = 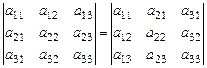. (9)

► Достаточно взглянуть на геометрическую схему формирования положительных членов определителя → лини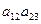и и 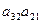меняются местами, сохраняя параллельность по отношению к главной диагонали определителя :

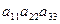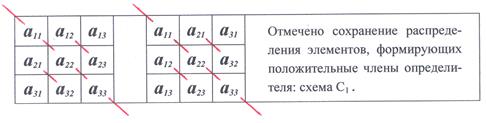
Так как положительные члены определителя не поменялись, то и отрицательные останутся теми же (можно было и для отрицательных членов отметить сохранение для соответствующих отрезков параллельности побочной диагонали).

Свойство 1 устанавливает полную равноправность строк и столбцов. Это значит, что в дальнейшем все свойства можно формулировать и для строк, и столбцов, но доказывать только для строк (или только для столбцов). ◄

Свойство 2. Перестановка двух строк (или столбцов) определителя равносильна умножению его на число –1.

► Переставим строки 2 и 3:

= – – – + + + .

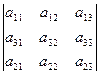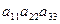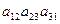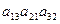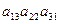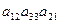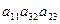Видим: все положительные члены определителя стали отрицательными, и наоборот. Это значит: если значение исходного определителя есть число d, то преобразованного → (– d). ◄

Свойство 3. Если определитель имеет две одинаковые строки (или два одинаковых столбца), то он равен нулю.

► Пусть в определителе строки 1 и 3 равны. Переставим их местами. Учитывая свойство 2, нужно заменить число d на число (– d). Но на самом деле определитель не изменился, так как мы переставили равные строки! Значит, нужно записать: d =– d. Но последнее равенство возможно только при d =0. ◄

Свойство 4. Умножение всех элементов некоторой строки (или столбца) определителя на число 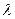равносильно умножению определителя на это число.

► Пусть 1-ю строку исходного определителя умножили на число :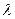

d = 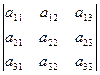→ 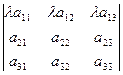= d ₁. (10)

Используя формулу для вычисления определителя, запишем:

d ₁= · + · + · – · – · – · =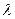

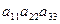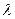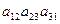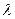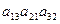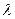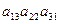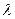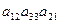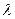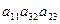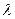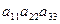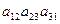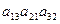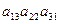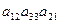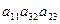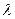= ·( + + – – – ) = · d. ◄

Следствие: общий множитель всех элементов некоторой строки (столбца) определителя можно выносить за знак этого определителя.

Свойство 5. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю.

► Свойство вытекает из свойства 4 при 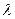=0. ◄

Свойство 6. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю.

► Это следует из последовательного применения свойства 4 (вынесение коэффициента пропорциональности за знак определителя) и свойства 3 (в определителе оказалось две равные строки). ◄

Свойство 7. Если каждый элемент строки- 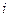(или столбца- 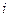) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей:

d = 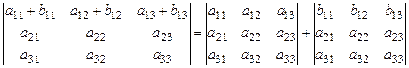= d ₁+ d ₂. (11)

► Используя формулу для вычисления определителя, запишем:

d = + + – – –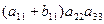

– = + + – – – +

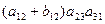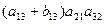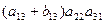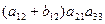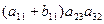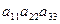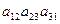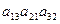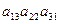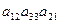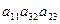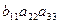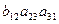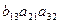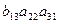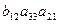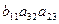+ + + – – – = d ₁+ d ₂. ◄

Свойство 8. Если к элементам некоторой строки (или столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель 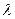, то величина определителя не изменится.

► Это следует из последовательного применения свойства 7 (разбить определитель на сумму двух определителей) и свойства 6 (второй определитель равен нулю, так как имеет две пропорциональные строки (два пропорциональных столбца)). ◄

Для установления следующего свойства определителя преобразуем его основную формулу вычисления:

d = 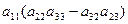– 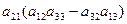+ 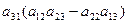. (12)

Чередование знаков у выделенных слагаемых имеет закономерность, которую удобно привязать к координатам элементов a ₁₁, a ₂₁, a ₃₁, а именно: для a ₁₁ → 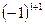, для a ₂₁ → 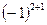, для a ₃₁ → 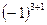. Это значит, что в выражении (12) знак слагаемого (+), если сумма i+j есть число чётное, и (-) – в противном случае. Теперь (12) можно записать в виде:

d = a ₁₁· 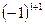· 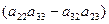+ a ₂₁· 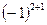· 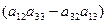+ a ₂₁· 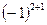· 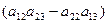. (13)

Используя определители 2-го порядка, выражение (13) запишем в компактной форме:

d = 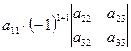+ + 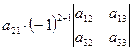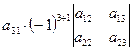. (14)

Из выражения (14) легко просматривается закономерность: если выделен элемент определителя a ₁₁, то в слагаемом используется определитель, который получается из исходного вычёркиванием строки-1 и столбца-1; если выделен элемент определителя a ₂₁, то в слагаемом используется определитель, который получается из исходного вычёркиванием строки-2 и столбца-1; если выделен элемент определителя a ₃₁, то в слагаемом используется определитель, который получается из исходного вычёркиванием строки-3 и столбца-1.

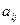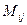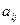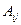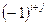
Таким образом, установлено соответствие: → определитель , который называют минором для элемента . Для получения ещё более записи для вычисления определителя введём обозначение: = 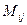, которое договорились называть алгебраическим дополнением для элемента 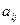. С учётом принятых обозначений перепишем формулу (14):

d = 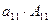+ + 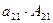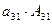. (15)

Запись (15) называют разложением определителя по столбцу-1: определитель равен сумме произведений элементов столбца-1 на соответствующие алгебраические дополнения элементов этого столбца. Аналогично получаем разложения для всех столбцов:

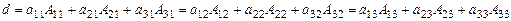, (16)

учитывая свойство 1, запишем также разложения определителя по строкам:

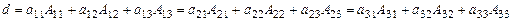. (17)

Рассматривая свойства определителя 3-го порядка, мы никак не учитывали задачу решения системы уравнений с тремя неизвестными. Теперь вспомним, что при решении системы уравнений с двумя неизвестными, мы в определителе d системы заменяли то 1-й, то 2-й столбец на столбец правых частей уравнений. А что будет происходить с определителем 3-го порядка, если в нём заменять столбцы? Воспользуемся записью (16) и заменим 1-й столбец произвольными числами h _1, h _2, h ₃: 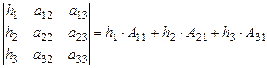. (18)

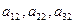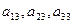Формально в (18) можно вместо чисел h _1, h _2, h ₃ взять элементы или столбцов 2 и 3 определителя. Так как и в первом, и во втором случаях получим определитель с равными столбцами, то по свойству 3 должны записать:

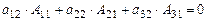, (19)

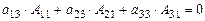. (20)

Учитывая результаты, представленные в выражениях (12)÷(20), определим самое важное свойство определителя, позволяющее получить формулы Крамера для систем уравнений с тремя неизвестными!

Свойство 9. Определитель равен сумме произведений элементов какого-либо столбца (какой-либо строки) на соответствующие алгебраические дополнения элементов этого столбца (строки); определитель равен нулю, если взята сумма произведений элементов одного столбца (строки), а алгебраические дополнения составлены для элементов другого столбца (строки).

Итак, перейдём от формальной конструкции определителя 3-го порядка и его формальных свойств к конкретным приложениям. Пусть имеем систему трёх линейных уравнений с тремя неизвестными x _i, 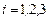: 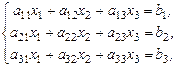(21)

где 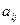, 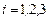; 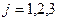– коэффициенты при неизвестных x_i (элементы некоторого числового поля) и b _i, 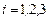– свободные члены (правые части уравнений) считаются заданными.

Системе уравнений (21) соответствуют: матрица системы A (составлена из коэффициентов при неизвестных) и расширенная матрица 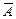(составлена из всех ее коэффициентов, включая свободные члены): 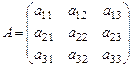, 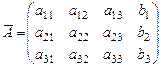. (22)

Используя свойства определителей 3-го порядка, преобразуем систему уравнений так, чтобы было выделено уравнение, в которое входит только одна неизвестная переменная x ₁. Для этого умножим первое уравнение системы (21) на алгебраическое дополнение А ₁₁, второе на A ₂₁, третье на A ₃₁ и сложим полученные уравнения:

+ =

= ,

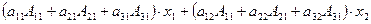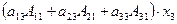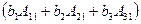или: 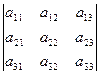· x ₁ + 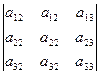· x ₂+ 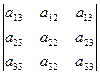· x ₃ = ,

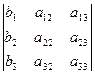после чего в соответствии со свойством 9 и с учётом принятых в формулах Крамера обозначений, можем записать: → .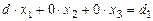

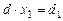Аналогично получаем выражения для неизвестных x ₂ и x ₃: , ,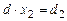

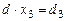где выражения для правых частей уравнений записываем, как и в случае систем уравнений для двух неизвестных: d ₂ = 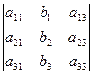, d ₃ = .

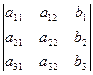Если проанализировать все вычислительные операции, используемые при переходе от записи системы уравнений (21) до записи выражений:

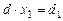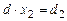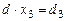, , , (23)

то следует отменить тот факт, что они всегда выполнимы.

Дальнейшие действия по поиску решений 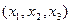системы уравнений (21) будут зависеть от того, какие значения реализует совокупность: .

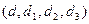При исследовании системы уравнений (1) для двух неизвестных x ₁, x ₂ исследование совокупности 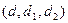проводилось сначала средствами алгебры, а затем иллюстрировалось геометрическими образами: прямыми. Исследования совокупности 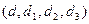для случая системы уравнений (21) с использованием только средств алгебры могут показаться излишне формальными. Поэтому все ситуации для совокупности 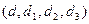сопровождаются геометрическими иллюстрациями.

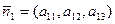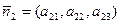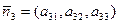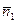
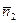
В геометрии каждому линейному уравнению системы (21) соответствует плоскость. Найти решение системы, значит найти точки, принадлежащие одновременно всем трем плоскостям: α ₁, α ₂, α ₃. Известно, что каждой плоскости соответствует вектор нормали. В нашем случае: , и – строки коэффициентов уравнений и опре­де­ли­теля d. 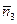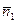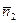Используя определение смешанного произведения векторов , нетрудно заметить, что 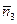= = 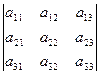d ≠0 равносильно утверждению, что векторы 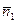, , 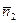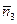– некомпланарные → единственность точки, общей трём плоскостям, в этом случае очевидна! Но, эта точка 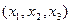и есть решение системы уравнений (21).

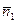
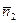
Если 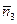= d =0, то векторы 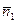, , 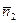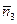– компланарны! Каким будет взаимное расположение плоскостей α ₁, α ₂, α ₃ в этом случае, и как представится соответствующее ему решение системы – наиболее трудоёмкая часть исследований!

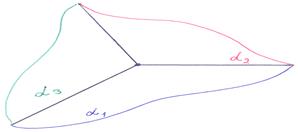1*. Пусть d ≠0. В этом случае решение системы (21) может быть записано при помощи формул Крамера (используются выражения (23)):

, , .

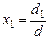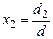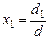Полученные формулы определяют единственное решение (т.к. отношение двух чисел, принадлежащих полю вещественных чисел, определяет единственное число!).

2*. Пусть d =0. В этом случае выразить x ₁, x ₂ и x ₃ из выражений (23) не удаётся: деление на нуль не определено в поле вещественных чисел. Чем может закончиться решение системы уравнений в этом случае?

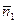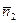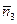1) , и – компланарны, но плоскости α ₁, α ₂, α ₃ раз­личны: линии их пересечения параллельны → общей точки 3-х плоскостей нет. Следует: система несовместна.

Для исследования соответствия геометрического образа и системы коэффициентов матрицы 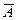рассмотрим 4-мерные векторы:

,

,

.

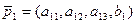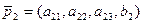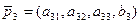В этом случае 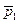, , 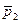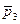– линейно независимы, и поэтому имеем: определители d ₁ ≠0, d ₂ ≠0, d ₃ ≠0.

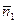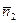2) , и 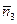– компланарны, но плоскости α ₁, α ₂, α ₃ раз­личны: линии их пересе­чения совпадают (пучок плоскостей!); общие точки трех плоскостей: общая ли­ния пересечения. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

Для исследования соответствия геометрического образа и системы коэффициентов матрицы 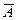воспользуемся 4-мерными векторами: ,

,

.

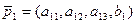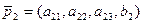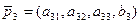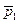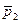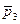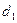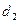В этом случае векторы , , – линейно зависимы, причём так, что один из них является линейной комбинацией двух других: это следует из уравнения пучка плоскостей! Учитывая свойства определителя имеем: =0, =0, 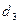=0. Это значит, что фактически система состоит из двух уравнений, и одной из переменных можно присваивать произвольные значения!

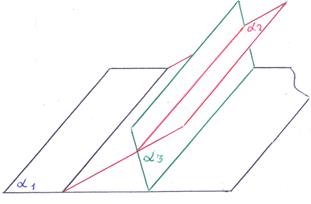
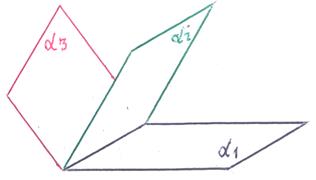
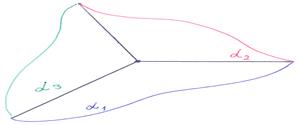
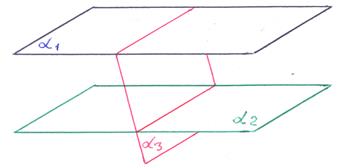3) 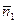|| 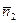, но плоскости α ₁, α ₂, α ₃ раз­личны: плоскость α ₃ пересекает параллельные плоскости α ₁, α ₂ по двум параллельным прямым. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: ,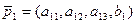

,

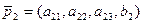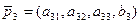
линейно независимы! Учитывая свойства определителя, получим: d ₁ ≠0, d ₂ ≠0, d ₃ ≠0.

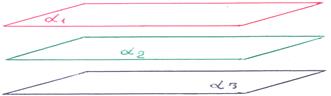
4) 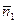|| 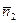и плоскости α ₁, α ₂ совпа­дают: линия пересечения плоско­сти α ₃ с плоскостями α ₁, α ₂ есть об­щие точки всех 3-х плоскостей. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

В соответствии с геометрическим образом, представленном на рисунке, векторы:

, ,

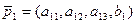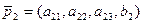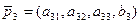
линейно зависимы! Учитывая свойства определителя: d ₁ =0, d ₂ =0, d ₃ =0.

5) 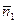|| || 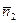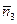, но плоскости α ₁, α ₂, α ₃ различны (и параллельны): плос­кости α ₁, α ₂, α ₃ не имеют общих то­чек. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы:

, ,

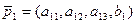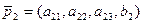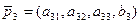
линейно независимы! Учитывая свойства определителя, получим: d ₁ ≠0, d ₂ ≠0, d ₃ ≠0.

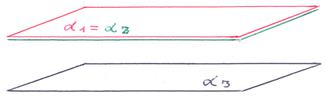6) 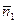|| || 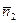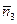, плоскости α ₁, α ₂ совпа­дают, плоскость α ₃ им параллельна: плоскости α ₁, α ₂, α ₃ не имеют об­щих точек. В этом случае система не имеет решений, говорят – система несовместна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: , ,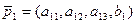

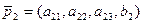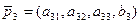
линейно независимы! Учитывая свойства определителя, получим: d ₁ ≠0, d ₂ ≠0, d ₃ ≠0.

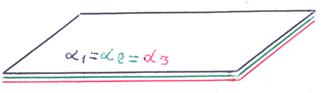7) 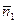|| || 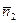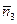, и плоскости α ₁, α ₂, α ₃ совпадают: все точки одной из плоскостей α ₁, α ₂, α ₃ принадлежат двум другим. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

В соответствии с геометрическим образом, представленном на рисунке, векторы: , ,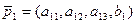

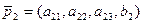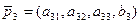
коллинеарны! Это значит: фактически имеем одно уравнение с тремя неизвестными, и двум из переменных можно присваивать произвольные значения. Учитывая свойства определителя, получим: d ₁ =0, d ₂ =0, d ₃ =0.

Общие выводы к решению системы 3-х линейных уравнений с 3-мя неизвестными:

1*. Если d ≠0: система уравнений имеет единственное решение.

2*. Если d =0: возможны случаи:

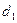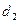▫ система уравнений имеет бесчисленное множество решений, если =0, 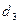=0, =0;

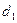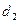▫ система уравнений не имеет решений, если ≠0, 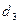≠0, ≠0;

Замечания: 1) учтем, что нумерация уравнений определяется автором задачи, и потому нет смысла выделяемые свойства одного или двух уравнений прокручивать во всех возможных циклических перестановках номеров уравнений: 1, 2, 3;

2) анализ системы уравнений (24) алгебраическими средствами не может «показать» характерные особенности каждого из выделенных случаев;

3) геометрическое решение системы уравнений (24) позволит достаточно наглядно выделить особенности каждого из случаев.

Представляет интерес рассмотреть частный случай системы уравнений с тремя неизвестными: 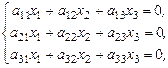(24)

когда все свободные члены системы уравнений (21) b ₁, b ₂, b ₃ = 0. В этом случае систему уравнений называют однородной.

Система (24) всегда имеет решение, так как все плоскости проходят через начало координат. Но и без геометрических соображений видно, что тройка чисел (0,0,0) является решением. Возникает вопрос: не имеет ли система других решений?

1*. Пусть d ≠0. В этом случае решение системы (24) может быть записано при помощи формул Крамера (используются выражения (23)):

, , .

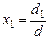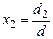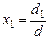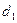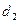Полученные формулы определяют единственное решение. Так как для системы уравнений (24) всегда =0, =0, 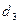=0, то решение нулевое: (0,0,0). Это же следует и из геометрических образов!

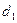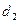2*. Пусть d =0. И в этом случае отмечаем выполнение условий: =0, =0, 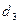=0. В соответствии с общими выводами решений должно быть бесчисленное множество!

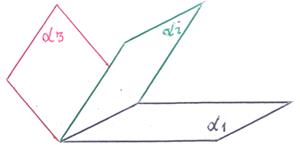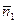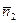1) , и 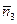– компланарны, но плоско­сти α ₁, α ₂, α ₃ раз­личны и составляют пучок плоскостей. В этом случае уравнения линейно зависимы: одно из уравнений (любое!) является следствием двух дру­гих. Это следует из уравнения пучка плоскостей! Плоскости пересекаются по общей прямой.

Это значит, что фактически система состоит из двух уравнений, и одной из переменных можно присваивать произвольные значения! В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

.

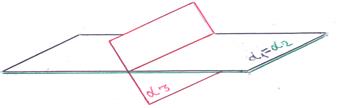2) 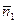|| 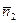и плоскости α ₁, α ₂ совпа­дают: линия пересечения плоско­сти α ₃ с плоскостями α ₁, α ₂ есть об­щие точки всех 3-х плоскостей. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

Это значит, что фактически система состоит из двух уравнений, и одной из переменных можно присваивать произвольные значения!

3) 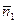|| || 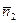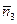, и плоскости α ₁, α ₂, α ₃ совпадают: все точки одной из плоскостей α ₁, α ₂, α ₃ принадлежат двум другим. В этом случае система имеет бесчисленное множество решений, говорят – система неопределенна.

Это значит: фактически имеем одно уравнение с тремя неизвестными, и двум из переменных можно присваивать произвольные значения.

Ввиду частого использования, рассмотрим случай, когда система (24) сведена к двум независимым уравнениям:

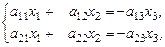(25)

причем в этой записи считаем, что не равен нулю определитель:

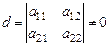, (26)

Далее, учитывая, что 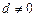, используя формулы Крамера, запишем выражения для неизвестных:

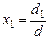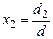, , (27)

присваивая произвольные значения переменной x ₃. После простейших преобразований, учитывающих свойства определителей получим:

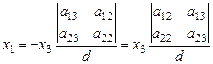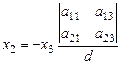, , (28)

Учитывая, что неизвестные x ₁, x ₂, x ₃ участвуют в уравнениях равноправно, попробуем найти для их вычисления симметричные выражения. Рассмотрим произвольный, не равный нулю определитель:

,

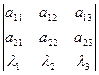где λ ₁, λ ₂, λ ₃ – произвольные числа (которые дальше не используются). Алгебраические дополнения определителя к элементам λ ₁, λ ₂, λ ₃ обозначим так:

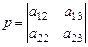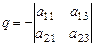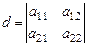, , . (29)

Используя (29), получим симметричные выражения для вычисления неизвестных x ₁, x ₂, x ₃:

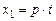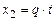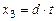, , , (30)

где t может принимать произвольные значения. Если параметр t определить как время, и принять, что при значении t = 0 некоторая точка находилась в начале координат (0,0,0), то, двигаясь со скоростью v =(p, q, d), в момент времени t движущаяся точка будет находиться в точке X (x ₁, x ₂, x ₃).

Замечания: 1) использование определителей 3-го порядка для «алгебраического» исследования систем линейных уравнений иллюстрирует их широкие возможности в теории и практических приложениях;

2) полученные результаты анализа возможных решений систем линейных неоднородных (общий случай) и однородных (частный случай) уравнений с тремя неизвестными послужат удобной иллюстрацией при изучении систем линейных уравнений с произвольным числом неизвестных.

Приведённые ниже примеры иллюстрируют важнейшие из вопросов, рассмотренных в теории определителей 3-го порядка.

☺☺

Пример 2 – 11: Вычислить определитель: .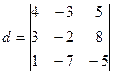

Решение:

Вычислим определитель несколькими способами:

Способ 1. В соответствии с определением определителя 3-го порядка:

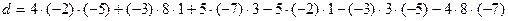=100.

Способ 2. В соответствии со свойством 9 можно вычислить определитель 3-го порядка разложением по любой строке или любому столбцу. Запишем разложение по 1-й строке:

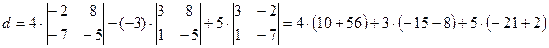=100.

Способ 3. Используя все необходимые свойства определителя, преобразуем его до простейшего вида: в одной из строк, ил