| Испытание | Случайное событие |
| 1. Бросание монеты. 2. Бросание игральной кости. 3. Стрельба по мишени. 4. Извлечение шара из урны. 5. Проверка качества изделий. 6. Рождение ребенка. | Появление герба или цифры. Выпадение какого-либо числа очков. Попадание, промах, выбивание определенного числа очков. Появление шара определенного цвета или номера. Изделие бракованное или стандартное. Пол ребенка. |
Виды случайных событий.
Определение 1. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. В противном случае события называются несовместными.
Примеры. __________________________________________________________
1) Испытание − бросание двух монет. События «герб появился на первой монете» и «герб появился второй монете» − совместные.
2) Испытание − бросание монеты. События «появился герб» и «появилась цифра» − несовместные.
Определение 2. Два события A и B называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Обозначение: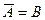 
, 
.
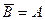Примеры. __________________________________________________________
1) A− выпадение герба,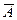 
− выпадение цифры.
2) A− попадание в цель, 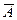− промах.
3) A− рождение мальчика, 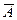− рождение девочки.
Определение 3. Несколько событий образуют полную группу, если появление одного и только одного из них в результате испытания является достоверным событием.
Примеры. __________________________________________________________
1. Пусть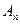 
− выпадение n очков при бросании игральной кости. Тогда
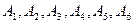−полная группа событий.
2. Два стрелка делают по одному выстрелу. Обозначим: попадание «+»,
промах «−». Запишем полную группу событий: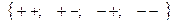 
.
3. Противоположные события − пример полной группы событий.
Классическое определение вероятности
Несколько событий, связанных с данным испытанием называются элементарными исходами испытания, если:
1) эти события образуют полную группу, т.е. при каждом осуществлении опыта наступает одно и только одно из них;
2) эти события являются равновозможными.
Те элементарные исходы, при которых событие A наступает, называются благоприятствующими событию A.
Пример.___________________________________________________________
Испытание − бросание игральной кости. События 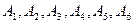−всевозможные элементарные исходы испытания. Пусть событие A − на игральной кости выпало менее пяти очков. События 
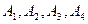− элементарные исходы, благоприятствующие появлению события A.
Определение. Вероятностью события A называется отношение числа m элементарных исходов, благоприятствующих событию A, к общему числу n всевозможных элементарных исходов испытания.
|
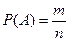
Примеры_________________________________________________________
1. Испытание − бросание монеты. Событие A− выпадение герба.
Так как n =2; m =1, то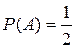 
.
2. Испытание − бросание игральной кости. Событие A − на игральной кости выпадет менее 3 очков. Это испытание имеет следующие элементарные исходы: {1; 2; 3; 4; 5; 6}. Из них событию A благоприятствуют исходы {1; 2}. Поэтому n =6, m =2. Значит,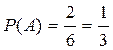 
.
3. В урне 4 белых и 6 черных шаров. Наугад вынимают один шар.
Событие A− этот шар белый.Так как n =10, m =4, то P(A)=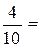 
0,4.
Свойства вероятности.
10 .Вероятность случайного события есть неотрицательное число,
заключенное между нулем и единицей: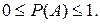 
□ Число элементарных исходов, благоприятствующих наступлению
события, удовлетворяет неравенству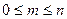 
. Поэтому 
.
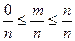Значит,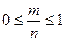 
. Следовательно, ■
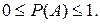20. Вероятность достоверного события равна 1.
□ Если событие U достоверное, то ему благоприятствует любой исход
испытания, поэтому m=n. Следовательно,
. ■
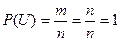30. Вероятность невозможного события равна 0.
□ Если событие V невозможное, то ни один из исходов испытания
не благоприятствует ему. Следовательно, m= 0. Тогда
. ■
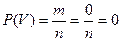40. Сумма вероятностей противоположных событий равна 1,
т.е.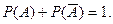 
□ Если событию A благоприятствует m исходов испытания, то событию
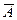благоприятствует n−m исходов испытания. Поэтому
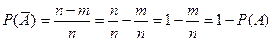. Значит,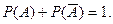
Если обозначить P(A)=p,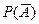 
=q, то p+q= 1. ■
Статистическое определение вероятности.
Пусть произведено N испытаний, при этом событие A наступило ровно M раз. Отношение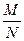 
называется относительной частотой события A и обозначается 
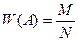. За вероятность события A принимается число, около которого группируются наблюдаемые значения относительной частоты: 
.
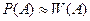Пример.___________________________________________________________
Английский ученый Пирсон произвел 23 000 бросаний монеты. При этом герб появился 11 512 раз. Значит, относительная частота появления герба равна
.
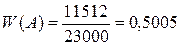Этот пример показывает, что за вероятность появления герба можно взять число 0,5.