При программной реализации алгоритмов циклической структуры в Mathcad используется два типа циклов for и while, которые добавляются в программу посредством команд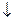 
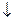for и while панели инструментов Programming.
Добавить цикл for в программу можно, используя команду for на панели Programming.
При организации цикла обычно внутри цикла определяют переменные, которые используют только в цикле. Такие переменные называют локальными и их значения определяются специальным оператором локального присвоения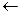 
. Следует помнить, что за пределами цикла они становятся неопределенными.
Пример 2.
Задан вектор 
. Вычислить сумму значений элементов вектора. Вывести результат на экран.
Алгоритм вычисления суммы значений элементов вектора имеет циклическую структуру и может быть реализован с использованием оператора for.
В Mathcad -документе программа будет следующей.
В программе переменная 
является локальной и значение вычисленной суммы не сохраняется после выхода из программы. Для сохранения вычисленного значения суммы использована переменная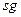 
.
Содержание задания
Разработайте блок-схемы алгоритмов и напишите программы для решения задач. Выполните тестирование программ.
Задача 1.
Вычислить значения функции 
, если значения аргументов заданы (см. вариант приложение Г).
Задача 2.
Разработать блок-схему алгоритма циклической структуры для вычисления функции в соответствии с вариантом задания (см. приложение Д, таб. Д.1). Написать и отладить программу в соответствии с блок-схемой в Mathcad.
Содержание отчета
- цель работы;
- задание;
- результаты решения задач.
- выводы.
Контрольные вопросы
1. Для каких целей используется панель инструментов Programming. Назовите команды панели, которые известны Вам.
|
|
2. Объясните работу оператора if.
3. Назовите типы циклических структур и, с использованием каких операторов, они реализуются в Mathcad.
Лабораторная работа №5. Решение уравнений с использованием численных методов
Цель работы
- изучение основ алгоритмизации инженерных задач;
- получение навыков в построении итерационных алгоритмов;
- изучение основных численных методов решения уравнений.
5.2. Краткие теоретические сведения
Пусть дано уравнение в виде
(1)
где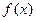 
– некоторая функция, которая может быть алгебраической или трансцендентной. В общем случае функция 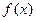может быть задана не формулой, а таблицей значений, производная может даже не существовать в некоторых точках.
Для получения решения уравнения (1) графическим методом необходимо исходное уравнение преобразовать к виду
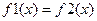(2)
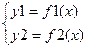(3)
Далее построить графики функци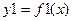и 
и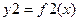 
. Точки пересечения кривых являются грубыми приближениями корней уравнения (1).
Найденные приближения позволяют найти отрезки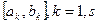 
, содержащие изолированные корни уравнения (1).
В результате реализации алгоритма метода половинного деления, после 
итераций получаем приближенное значение корня 
и исходный отрезок 
на -ой будет равен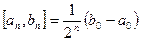 
.
В результате реализации алгоритма метода Ньютона, используя итерационную формулу
,
Получаем приближенное решение уравнения (1).
Содержание задания
Получить решение уравнения (см. приложение Е) с использованием метода половинного делении и метода Ньютона. Представить в Mathcad -документе результаты выполнения четырех итераций по каждому из указанных методов.
|
|
Содержание отчета
- цель работы;
- задание;
- итерационная формула метода половинного деления и результаты выполнения четырех итераций;
итерационная формула метода Ньютона и результаты выполнения четырех итераций;
- выводы.
5.5. Контрольные вопросы
1. Какие существуют численные методы решении уравнений.
2. Дайте геометрическую интерпретацию метода половинного деления (метода дихотомии).
3. Запишите итерационную формулу метода половинного деления.
4. Дайте геометрическую интерпретацию метода итераций.
5. Запишите итерационную формулу метода итераций.
6. Дайте геометрическую интерпретацию метода Ньютона.
7. Запишите итерационную формулу метода Ньютона.
8. Объясните какими способами можно получить решение уравнения в Mathcad.