В процессе экспериментальных исследований получают статистический ряд измерений. Например, для функции двух переменных у = f (х) каждому значению функции у 1,…, у n соответствует определенное знание аргумента х 1,…, х n. На основе экспериментальных данных можно подобрать алгебраические выражения, которые называют эмпирическими формулами. Такие формулы содержат постоянные величины, установленные по опытным данным, они имеют ограниченную область применения, которая не должна выходить за пределы эксперимента. Тем не менее, эмпирические формулы имеют очень большое значение и весьма широко применяются. Необходимость в подборе эмпирических формул возникает, кроме того, при замене сложного аналитического выражения, которое требует громоздких вычислений, упрощенной эмпирической зависимостью. Часто эмпирические формулы незаменимы для анализа измеренных величин. 
Таким образом, эмпирические формулы являются приближенными выражениями аналитических зависимостей. Замену точных аналитических выражений называют аппроксимацией, а функции – аппроксимирующими.
 |
Процесс подбора эмпирических формул состоит в следующем. Вначале на сетку прямоугольных координат наносят данные измерений, соединяет точки плавной кривой, и выбирают её вид, а затем вычисляют параметры формул. Вид формулы по возможности должен быть простым. Наиболее часто встречающиеся виды графиков эмпирических формул представлены на рис. 6.2.
Аппроксимация экспериментальных данных прямолинейной функцией (рис. 6.2, а) позволяет наиболее просто установить эмпирическую формулу, поэтому при анализе графического материала линейную функции часто используют. Ее также широко применяют для линеаризацию кривых с помощью полу – или логарифмических координатных сеток.
Если экспериментальный график имеет вид, представленный на рис. 6.2, б, то необходимо применить формулу  , заменяя
, заменяя  и,
и,  , имеем
, имеем  , т.е. прямую на логарифмической сетке.
, т.е. прямую на логарифмической сетке.
Если график имеет вид кривых на рис. 6.2, в, то можно использовать выражение  , которое линеаризуется на полулогарифмической сетке, заменяя
, которое линеаризуется на полулогарифмической сетке, заменяя  :
:  .
.
При подборе эмпирических формул широко используются полиномы
 , (6.1)
, (6.1)
где А 0, …, Аn – постоянные коэффициенты.
Полиномами можно аппроксимировать любые результаты измерений, если они графически представляют собой непрерывные функции. Даже при неизвестном выражении (6.1), вид функции можно определить, применяяметоды средних и наименьших квадратов.
Построение эмпирических зависимостей по табличным данным. Рассмотрим последовательность построения эмпирических зависимостей между исследуемыми величинами х и у, если они заданы таблицей экспериментальных данных. В качестве примера возьмем результаты лабораторного определения величины коэффициента крепости по шкале М.М. Протодьяконова и соответствующие им значения контактной прочности (твердость) по Л.Н. Барону, определяемой путем вдавливания плоского штампа диаметром 2-3 мм в нешлифованную поверхность образца (табл. 6.1).
За независимую переменную примем коэффициент крепости горных пород f, а за функцию – контактную твердость Р k. Разобьем интервал изменения f на n = 50 одинаковых частей, для чего вначале определим шаг разбивки с использованием формулы Стэрджеса:
 .
.
Принимаем интервал изменения коэффициент крепости пород от 0 до 20 с шагом разбивки n = 2, и строим на основании этого табл. 6.2, где средним значениям Р kі в каждом і -м интервале соответствует среднее значение f і. С использованием средних построена табл. 6.3, где первые ( ), вторые (
), вторые ( ) и третьи (
) и третьи ( ) разности определяются по формулам:
) разности определяются по формулам:
Таблица 6.1 – Результаты лабораторного определения
коэффициента крепости и контактной твердости горных пород
| Горные породы | Коэффициент крепости | Контактная твердость, МПа |
| Уголь марки Т Руда гематитовая Уголь марки Ж Уголь марки К Уголь марки Г Антрацит Руда полиметаллическая Сланец углистый Аргиллит углистый Песчаник крупнозерничтый Руда анатитовая Мергель Песчаник среднезернистый Песчаник сланцевый Известняк некрепкий Доломит Сланец песчаный Фосфорит Алевролит Известняк Аргиллит Периодит Песчаник мелкозернистый Скарн Габро-диабаз Габро Гранодиорит Порфир Сленит Туф Туфбрекция Кварцит Мрамор Альбитофир Базальт Гранит Диорит Бренчия Диорит Порфирит Роговик Гранит лециоуратовый Гранодиорит серый Гранодиорит розовый Кальцито-флюорит Монцонит альбитизованый Гранатовый скарн Диабаз Гранит окварцованый Гранадиорит метаморфизованый | 0,6 0,6 0,7 1,2 1,5 1,8 1,6 2,2 2,7 3,7 3,0 4,0 3,1 5,0 4,5 4,2 4,3 6,3 6,4 6,6 5,3 7,0 7,8 6,5 7,9 9,6 8,2 9,5 9,6 9,3 8,7 8,8 8,9 12,0 10,2 11,0 11,0 10,1 13,3 13,6 13,5 14,8 15,2 15,9 14,3 16,8 17,2 19,1 19,4 18,6 |
 МПа;
МПа;
 МПа;
МПа;
 МПа;
МПа;
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
 МПа;
МПа;
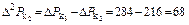 МПа;
МПа;
¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼¼
 МПа и т.д.
МПа и т.д.
Полагая, что  , искомую зависимость можно записать в виде ряда:
, искомую зависимость можно записать в виде ряда:
 . (6.2)
. (6.2)
Если в табл. 6.3 разности m -го порядка находятся в пределах точности эксперимента, то m + 1 разности можно не рассчитывать, а для m- х следует найти их среднее значение.
В нашем случае вторые разности можно считать стабильными, а их среднее значение равно:
 .
.
После подстановки в (6.2) значений получим
 .
.
Преобразовав выражение, получим эмпирическую форму, связывающую показатель контактной твердости пород с коэффициентом крепости:
 . (6.3)
. (6.3)
Зависимость (6.3) представляет собой квадратичный трехчлен, часто используемый для аппроксимации многих зависимостей.
Таблица 6.2 Средние значения параметров f и P u
| Интервалы f | 
| 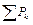
| n |  ,
МПа ,
МПа
|
| 0…2,0 2,1…4,0 4,1…6,0 6,1…8,0 8,1…10,0 10,1…12,0 12,1…14,0 14,1…16,0 16,1…18,0 18,1…20,0 | 1,0 3,0 5,0 7,0 9,0 11,0 13,0 15,01 17,0 19,0 | 17+15+32+49+68+90+75=346 130180154+190+248+280=1165 397+531+303=1231 603+595+618+759+710+843+633+861+626=6248 1151+882+1131+1154+2091+974+993+1014=8390 1733+1319+1497+1489+1310=7348 1915+1995+1969=5879 2443+2562+2776+2298=10079 3082+3215=6297 38870+3980+3690=11540 |
Таблица 6.3 Расчет разностей
| Аргументы | Функции | Первые разности | Вторые разности | Третьи разности |

| 
| 
| 
| 
|

| 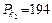
| 
| 
| 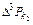
|

| 
| 
| 
| 
|
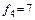
| 
| 
| 
| 
|
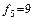
| 
| 
| 
| 
|

| 
| 
| 
| 
|

| 
| 
| 
| 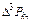
|

| 
| 
| 
| 
|
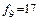
| 
| 
| 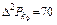
| 
|

| 
| 
| 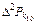
| 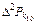
|
Метод средних. Метод средних основан на следующем предположении. Если по экспериментальным точкам можно построить несколько плавных кривых, то наилучшей будет та кривая, у которой разностные отклонения наименьшие. Следовательно, подбор эмпирической формулы по методу средних основывается на условие равенства нулю всех отклонений функции от среднего значения, т.е.

 , (6.4)
, (6.4)
где  – единичное отклонение.
– единичное отклонение.
Последовательность нахождения коэффициентов эмпирической формулы по методу средних сводится к следующему:
а) на основании предварительного анализа результатов эксперимента устанавливают вид функции, в качестве которой чаще всего используют многочлен;
б) определяют число членов ряда, обычно ограничиваясь 3-4;
в) в принятое выражение подставляют все пары измеренных значений х і и у і для определения отклонений:

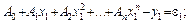
 (6.5)
(6.5)
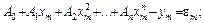
г) обычно число уравнений больше количества коэффициентов А, поэтому отклонения распределяют на столько групп, сколько неизвестных коэффициентов в уравнении;
д) приравнивая к нулю сумму отклонений для каждой из групп, получают систему линейных уравнений относительно искомых параметров А. Для решения систем уравнений в математическом обеспечении ПЭВМ имеются стандартные программы;
е) после определения численных значений коэффициентов проверяется качество аппроксимации сопоставлением знаний функции и экспериментальных точек.
Для иллюстрации метода средних воспользуемся результатами лабораторного определения коэффициента крепости и контактной твердости горных пород, представленных в табл. 6.1, а в качестве аппроксимационной формулы возьмем трехчлен (6.3):

Сгруппируем уравнения согласно табл. 6.4, а в пределах каждой группы сложим уравнения почленно и приравняем суммы к нулю:
 (6.6)
(6.6)
Таблица 6.4 – Расчет параметров эмпирического уравнения
методом средних

|  , МПа , МПа
| 
| 
| Группа точек |
| a + b + c– 49=0 9 a +3 b + c– 194=0 25 a +5 b + c– 410=0 49 a +7 b + c– 694=0 | I | |||
| 81 a +9 b + c– 1049=0 121 a +11 b + c– 1470=0 169 a +13 b + c– 1960=0 | II | |||
| 225 a +15 b + c– 2520=0 289 a +17 b + c– 3140=0 361 a +19 b + c– 3846=0 | III |
Решая систему (6.6), получим а = 8,59, b = 39,2; с = -0,39.
Таким образом, зависимость между параметрами может быть представлена формулой
 , (6.7)
, (6.7)
которая почти полностью совпадает с ранее полученным выражением (6.3), что свидетельствует от достаточной точности метода.
Метод наименьших квадратов. Наилучшие результаты при определении параметров заданного уравнения дает использование метода наименьших квадратов. Суть этого метода заключается в следующем. Если все измерения функции у 1,…, у 2 произведены с одинаковой точностью,а ошибки измерения соответствуют нормальному закону, то параметры исследуемого уравнения определяются из условия, что сумма квадратов отклонений измеренных значений от расчетных принимает наименьшее значение.
Если аппроксимирующее уравнение записать в виде
 , (6.8)
, (6.8)
а имеющиеся данные в точках х i обозначить через у i, то условием минимума суммы квадратов будет равенство:
S =  , (6.9)
, (6.9)
где п – число экспериментальных точек.
В математическом обеспечении современных ЭВМ имеются стандартные программы для аппроксимации экспериментальных данных методом наименьших квадратов. метод наименьших квадратов обеспечивает результаты высокой надежности.
Применение метода продемонстрируем на предыдущем примере для квадратного трехчлена
 , (6.10)
, (6.10)
параметры которого определяются из системы уравнений:
 (6.11)
(6.11)
Расчет коэффициентов эмпирического уравнения производится на основе табл. 6.5, используя данные последней строки для составления системы:

Таблица 6.5 – Расчет коэффициентов эмпирического уравнения методов наименьших квадратов
| № п/п | f i | 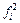
| 
| 
| f i  , МПа , МПа
| f i  ,
МПа ,
МПа
| 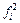 · ·  ,
МПа ,
МПа
|
| Всего |
После решения системы уравнений получим а = 8,6; b =38,9; с = 0,81, а формула запишется в виде:
 . (6.12)
. (6.12)
Сопоставляя (6.12), (6.7) и (6.3), убеждаемся, что коэффициенты при переменной f отличаются между собой не больше чем на 2 %, что свидетельствует о допустимой погрешности уравнений, полученных различными способами.
ЛЕКЦИЯ 15