Если две переменные зависят друг от друга так, что каждому значению х соответствует определенное значение у, то между ними существует функциональная и детерминированная связь. Если одному значению х соответствует несколько значений (совокупность) у, то такую связь называют стохастической. Стохастическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. В практике исследований часто рассматривается частный случай такой связи, называемый статистической связью. Об этой связи говорят тогда, когда условное математическое ожидание одной случайной переменной является функцией значения, принимаемого другой случайной переменной.
Зависимость между одной случайной переменной и условным средним значением другой случайной переменной называется корреляционной. Под корреляционным анализом понимают исследование закономерностей между явлениями (процессами), которые зависят от случайных факторов. Суть корреляционного анализа сводится к установлению уравнения регрессии, т.е. зависимости между случайными величинами, аргументом х и функцией у, оценке тесноты связи между ними, достоверности и адекватности результатов измерений.
Чтобы определить наличие связи между х и у строят так называемое корреляционное поле (рис. 6.3). По расположению точек и наклону средней линии уже визуально можно судить о наличии корреляционной связи. Так, очевидно, что с увеличением значений х на рис. 6.3 значения у увеличиваются. Следовательно, можно сделать вывод, то имеется положительная связь между х и у. Если на корреляционном полеусреднить точки, т.е. определить 
и 
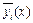, нанести эти точки на график и соединить их между собой, то получим ломаную линию (1), по виду которой можно судить, как в среднем меняется у в зависимости от изменения х. Такая линия называется эмпирической линией регрессии. По ее виду можно сделать предположение о форме связи. В данном случае ломаную линию можно аппроксимировать прямолинейной или криволинейной зависимостями.
 |
Если на корреляционном поле провести плавную линию, которая равноудалена от средних точек, то получим теоретическую регрессионную зависимость. Такую зависимость называют парной или однофакторной. В общем случае парная зависимость может быть аппроксимировала линией, параболой, логарифмической, степенной и показательной функциями, полиномом и др.
Линейная регрессия, или линейная форма связи между случайными переменными, занимает особое место в корреляционном анализе. При такой связи 
есть линейная функция
, (6.13)
где а 0 и а 1 – коэффициенты регрессии;
х – независимая случайная переменная.
Параметры в уравнении регрессии (коэффициенты регрессии) определяются по способу наименьших квадратов, т.е. при построении теоретической регрессионной зависимости оптимальной будет такая функция, у которой соблюдается условие
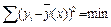, (6.14)
где 
– фактические ординаты поля;
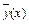– среднее значение ординаты с абсциссой х.
В случае линейной регрессии за теоретическое значение принимается величина, получаемая по формуле (6.13), т.е. ищется такая прямая линия, сумма квадратов отклонений измеренных значений у і от которой была бы минимальной:
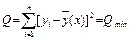. (6.15)
Как известно, минимум функции можно найти, приравняв к нулю ее первую производную. Запишем выражения (6.15) в виде
,
найдем частные производные функции Q по a 0 и a 1 , приравняем их нулю и составим систему нормальных уравнений
(6.16)
решая которую получаем значения коэффициентов регрессии
; 
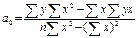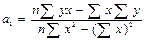. (6.17)
Зависимость (6.13) является частным случаем более общей нелинейной зависимости
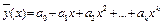. (6.18)
Коэффициенты регрессии а 0, а 1, … а k в (6.18) определяются аналогично по способу наименьших квадратов, в результате чего получим:
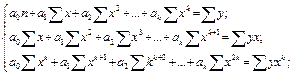(6.19)
Вычислив коэффициенты системы (6.19), ее можно решить любым известным методом.
В общем случае тесноту связи оценивают по отношению к общей дисперсии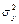 
, т.е. рассматривают отношение
(6.20)
где 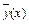– теоретическая функция регрессии;
– условное генеральное среднее;
М [] – математическое ожидание;
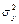– полная дисперсия;
– теоретическое корреляционное отношение.
Критерием близости корреляционной зависимости между х и у к линейной функциональной зависимости является коэффициент корреляции, который показывает степень линейности связи между х и у:
, (6.21)
где n – число измерений.
Коэффициент корреляции является частным случаем теоретического корреляционного отношения (6.20), когда связь между переменными х и у линейна. Значение коэффициента корреляции всегда меньше единицы. При r =1 переменные х и у связаны функциональной линейной связью.
На практике часто возникает потребность в установлении связи между у и многими параметрами х 1, х 2,…, х n. Многофакторные теоретические регрессии аппроксимируют полиномами первого или второго порядка. Уравнение регрессии определяет систематическую составляющую, а ошибки разброса – случайную. В этом случае для изучения связи между переменными используют несколько видоизмененный метод, а уравнение связи составляется между зависимой случайной величиной у и n переменными х. Для простоты рассуждений ограничимся линейной формой связи, представленной следующим уравнением регрессии:
, (6.22)
где х 1, х 2, … х n – переменные;
а 0 и а 1, …, а n – неизвестные параметры, называемые коэффициентами регрессии.
Метод, позволяющий по выборке, которая содержит отдельные измеренные значения переменных у и х 1, х 2, … х n, оценить значения неизвестных параметров а 0 и а 1, …, а n, называется множественной регрессией. Выражение (6.22) называется уравнением множественной линейной регрессии. Коэффициенты уравнения (6.22) так же, как и в случае двух признаков, определяют, исходя из принципа наименьших квадратов:
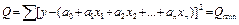. (6.23)
Последовательно дифференцируя (6.23) по а 0 и а 1, …, а n и приравнивая каждое из полученных выражений нулю, получают систему нормальных уравнений:
(6.24)
которую решают любым известным способом. Теоретическую модель множественной регрессии можно получить методами математического планирования активного эксперимента, а также пассивным способом, когда точки фактического пространства выбираются произвольно.