ТЕМА 5. КОМПЛЕКСНЫЕ ЧИСЛА. МНОГОЧЛЕНЫ

Комплексные числа. Операции с комплексными числами. Представление в прямоугольной системе координат. Многочлены. Корни многочленов с действительными коэффициентами.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

Комплексным числом z называется упорядоченная пара действительных чисел (а,b): z = (a,b) (термин «упорядоченная» означает, что в записи комплексного числа важен порядок чисел а и b: (a,b)≠(b,a)). При этом первое число а называется действительной частью комплексного числа z и обозначается a = Re z, а второе число b называется мнимой частью z: b = Im z.

Два комплексных числа z₁ = (a₁, b₁) и z₂ = (a₂, b₂) равны тогда и только тогда, когда у них равны действительные и мнимые части, то есть a₁ = a₂, b₁ = b₂.

Действия над комплексными числами.

1.Суммой комплексных чисел z₁ = (a₁, b₁) и z₂ = (a₂, b₂) называется комплексное число z = (a,b) такое, что a = a₁ + a₂, b = b₁ + b₂.

Свойства сложения:

а) z₁ + z₂ = z₂ + z₁;

б) z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃;

в) существует комплексное число 0 = (0,0): z + 0 = z для любого комплексного числа z.

1. Произведением комплексных чисел z₁ = (a₁, b₁) и z₂ = (a₂, b₂) называется комплексное число z = (a,b) такое, что a = a₁a₂ – b₁b₂, b = a₁b₂ + a₂b₁.

Свойства умножения:

а) z₁z₂ = z₂z₁;

б) z₁ (z₂ z₃) = (z₁ z₂) z₃,

в) (z₁ + z₂) z₃ = z₁ z₃ + z₂ z₃.

Замечание. Подмножеством множества комплексных чисел является множество действительных чисел, определяемых как комплексные числа вида (а,0). Можно убедиться, что при этом определение операций над комплексными числами сохраняет известные правила соответствующих операций над действительными числами. Кроме того, действительное число 1 = (1,0) сохраняет свое свойство при умножении на любое комплексное число: 1∙ z = z.

Комплексное число (0, b) называется чисто мнимым. В частности, число (0,1) называют мнимой единицей и обозначают символом i.

Свойства мнимой единицы:

1)i∙i=i² = -1; 2) чисто мнимое число (0,b) можно представить как произведение действительного числа (b,0) и i: (b,0) = b∙i.

Следовательно, любое комплексное число z = (a,b) можно представить в виде: (a,b) = (a,0) + (0,b) = a + ib.

Запись вида z = a + ib называют алгебраической формой записи комплексного числа.

Замечание. Алгебраическая запись комплексных чисел позволяет производить операции над ними по обычным правилам алгебры.

Комплексное число 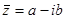называется комплексно сопряженным числу z = a + ib.

3.Вычитание комплексных чисел определяется как операция, обратная сложению: z =(a,b) называется разностью комплексных чисел z₁ = (a₁, b₁) и z₂ = (a₂, b₂), если a = a₁ – a₂, b = b₁ – b₂.

4.Деление комплексных чисел определяется как операция, обратная умножению: число z = a + ib называется частным от деления z₁ = a₁ + ib₁ и z₂ = a₂ + ib₂ (z₂ ≠ 0), если z₁ = z∙z₂. Следовательно, действительную и мнимую части частного можно найти из решения системы уравнений: a₂ a – b₂ b = a₁, b₂ a + a₂ b = b₁.

Геометрическая интерпретация комплексных чисел.

Комплексное число z = (a,b) можно представить в виде точки на плоскости с координатами (a,b) или вектора с началом в начале координат и концом в точке (a,b).

Запись вида

z = ρ (cos φ + isin φ)

называется тригонометрической формой записи комплексного числа.

В свою очередь, модуль и аргумент комплексного числа можно выразить через а и b: . Следовательно, аргумент комплексного числа определен не однозначно, а с точностью до слагаемого, кратного 2π.

Частным случаем операции умножения является возведение в степень:

формула Муавра.

Используя полученные соотношения, перечислим основные свойства комплексно сопряженных чисел:

Извлечение корня из комплексного числа.

Комплексное число называется корнем n-й степени из z, если z = z₁ⁿ.

Пример. Число z = 16 можно представить в тригонометрической форме следующим образом: z = 16(cos0 + isin0). Найдем все значения :

Показательная форма комплексного числа.

Введем еще одну форму записи комплексного числа. На множестве комплексных чисел существует связь между тригонометрическими и показательными функциями, задаваемая формулой Эйлера:

, Используя эту формулу, можно получить из еще один вид комплексного числа: который называется показательной формой записи комплексного числа.

Рассмотрим в комплексной области многочлен, то есть функцию вида

, где - комплексные числа. Числа называются коэффициентами многочлена, а натуральное число n – его степенью.

Два многочлена P_n (z) и равны тогда и только тогда, когда m=n, a₀ = b₀, a₁ = b₁,…, a_n = b_n.

Число z₀ называется корнем многочлена, если P_n (z₀) = 0.

Теорема (теорема Безу). Остаток от деления многочлена P_n(z) на z – z₀ (z₀ – не обязательно корень многочлена) равен P(z₀).

Теорема (основная теорема алгебры). Всякий многочлен в комплексной области имеет корень.

Вопросы для самопроверки

1.Что такое мнимая единица?

2. Что такое вещественная и мнимая части комплексного числа? Являются ли они вещественными числами?

3. Что такое комплексно сопряженные числа? Чем отличаются изображения комплексно сопряженных чисел z и z* на комплексной плоскости?

4. Как изобразить на комплексной плоскости, пользуясь правилами сложения векторов, сумму и разность двух комплексных чисел7

5. Чему равно произведение комплексно сопряженных чисел?

6. Сколько решений имеет квадратное уравнение с вещественными коэффициентами? какие характерные случаи возможны?

7. В каком виде может быть представлен многочлен. если известны его корни?