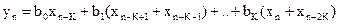.
Выразим Z – преобразование выходного сигнала фильтра через Z – преобразование входного сигнала
.
Разделив Y(z) на X(z), найдем системную функцию
.
Найдем комплексный коэффициент передачи фильтра, используя подстановку 
.
.
Обозначим
, (2.26)
где 
Тогда АЧХ и ФЧХ (без приведения в интервал от -π до π) фильтра определятся следующими соотношениями
,
. (2.27)
Так как второе слагаемое в выражении для ФЧХ - константа (0 или π), ФЧХ этого фильтра является линейно-ломаной.
Линейность ФЧХ обусловлена симметрией коэффициентов системной функции относительно середины линии задержки (симметрией импульсной характеристики фильтра).
2.12. Синтез нерекурсивного фильтра с линейной ФЧХ методом ряда
Фурье и «окна»
Задачей синтеза фильтра является определение коэффициентов его системной функции при заданных требованиях к АЧХ. В случае фильтра с линейной ФЧХ и АЧХ, определяемой рядом косинусов ((2.26), (2.27)), этими коэффициентами являются коэффициенты 
.
Из (2.26) видно, что функция 
, определяющая АЧХ фильтра, является периодической функцией с периодом 2π.
Пусть требуется выполнить синтез ФНЧ, у которого функция A(θ) стремится к функции D(θ), показанной на рисунке 2.29 в интервале изменения θ от –π до π.
Рисунок 2.29 – Идеальная АЧХ ФНЧ
Разложение функции D(θ) в ряд Фурье позволяет определить коэффициенты
, (2.32)
где m = 1,2..K.
В качестве примера приведем рассчитанные по формулам (2.32), (2.26) и (2.27) функцию 
и АЧХ К(θ) при θ0 = π / 2, K=3.
Рисунок 2.30 – Функция и АЧХ К(θ) при θ0 = π / 2, K=3
Вместе с графиком реальной АЧХ K(θ) показана идеальная прямоугольная АЧХ D(θ). При K=3 эти характеристики сильно отличаются друг от друга. Особенностью АЧХ являются пульсации как в полосе пропускания, так и в полосе задерживания.
На рисунках 2.31 и 2.32 приведены АЧХ фильтров при K=10 и K=20 соответственно.
Рисунок 2.31 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2, K = 10
Рисунок 2.32 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2, K = 20
На этих рисунках используется логарифмический масштаб по оси ординат для того, чтобы АЧХ была более наглядной в полосе задерживания.
Из рисунков видно, что увеличение длины линии задержки (уменьшение количества отбрасываемых членов разложения Фурье), делая АЧХ более прямоугольной, не устраняет пульсации АЧХ. С увеличением длины линии задержки частота пульсаций увеличивается, однако максимальный уровень первого бокового лепестка в полосе задерживания остается практически неизменным и равным 0.1.
Пульсации АЧХ вблизи точек разрыва функции, связанные с ограничением членов разложения в ряд Фурье, получили название явления Гиббса.
Для уменьшения пульсаций рядом специалистов по цифровой обработке сигналов было предложено использование так называемых «оконных функций».
Сущность метода состоит в следующем: вместо коэффициентов системной функции bm используют коэффициенты
,
где 
- m-ый отсчет оконной функции.
Простому ограничению ряда Фурье соответствует прямоугольное окно
Несколько других функций приведено в таблице 2.1.
На рисунках 2.33 и 2.34 показаны АЧХ рисунков 2.31 и 2.32 соответственно после операции сглаживания с использованием окна Хемминга. Из сопоставления АЧХ до сглаживания и после него видно, что эта операция приводит к существенному (примерно на 40 дБ) ослаблению пульсаций, но и к расширению переходной полосы между полосой пропускания и полосой задерживания фильтра.
Таблица 2.1. Функции окна
| Название окна | Функция окна |
| Окно фон Ганна (приподнятый косинус) |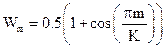 
|
| Окно Хемминга | 
|
| Окно Блэкмана | 
|
| Окно Ланцоша |  , где L - целое число
|
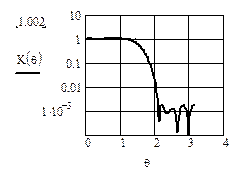
Рисунок 2.33 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2, K=10 и сглаживанием
пульсаций функцией Хемминга
Рисунок 2.34 – АЧХ фильтра с линейной ФЧХ при θ0 = π / 2, K=20 и сглаживанием
пульсаций функцией Хемминга
Описанный метод синтеза рассмотрен на примере фильтра нижних частот. Однако его нетрудно распространить на фильтры других типов.
Например, АЧХ полосового фильтра с граничными значениями полосы θ1 и θ2 можно представить в виде разности АЧХ ФНЧ, как это показано на рисунке 2.35.
Рисунок 2.35 – Представление АЧХ полосового фильтра в виде разности АЧХ ФНЧ
D(θ)=D2(θ) – D1(θ)
Такое представление АЧХ позволяет определить коэффициенты разложения в ряд Фурье bm как разность соответствующих коэффициентов разложений в ряд Фурье АЧХ ФНЧ
. (2.33)
Аналогичным образом находятся коэффициенты разложения для режекторного фильтра (РФ) и фильтра верхних частот (ФВЧ)
В таблице 2.2 приведены значения коэффициентов разложения АЧХ для всех типов фильтров. Оконные функции используютcя при синтезе всех типов фильтров одинаково.
Таблица 2.2. Коэффициенты разложения в ряд Фурье функции,
определяющей АЧХ фильтра
| Тип фильтра | Коэффициенты bn |
ФНЧ 
| 
|
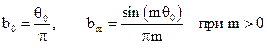
ФВЧ
|
 
|
ПФ
|
|
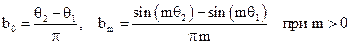
РФ
|
|
2.13. Синтез нерекурсивных фильтров с линейной ФЧХ методом
наименьших квадратов
На рисунке приведена функция D(θ) - идеальная АЧХ полосового фильтра в полосе пропускания и полосе задерживания и функция A(θ), описывающая реальную АЧХ.
Рисунок 2.36 - Функция A(θ) и функция D(θ), описывающая идеальную АЧХ
Функция D(θ) определяется следующим образом
Метод не накладывает ограничений на АЧХ в переходной полосе.
Функция A(θ) определяет АЧХ реального фильтра, т.к. АЧХ 
Можно считать, что при минимальном отличии функции A(θ) от функции D(θ), отличие АЧХ от D(θ) будет также минимальным.
Сформируем целевую функцию
. 
Функция g(q) под знаком интеграла представляет собой весовую функцию, регулирующую точность аппроксимации.
Пусть, например,
При g<1 пульсации АЧХ в полосе пропускания меньше, чем в полосе задерживания, а при g>1 наоборот.
Условием минимума d является равенство нулю производных
Частная производная по коэффициенту Сm равна
где m = 0, 1,.. K.
Подставляя в последнее соотношение W(θ) и D(θ) и приравнивая производную нулю, получим
Поменяв местами операции суммирования и интегрирования, выполнив интегрирование и полагая m=0,1,2,…K, получим систему из K+1 уравнения с K+1 неизвестным коэффициентом Ck.
Решение этой системы завершает синтез фильтра.
2.14. Метод наилучшей равномерной (чебышевской) аппроксимации
Все методы, рассмотренные выше, позволяют синтезировать фильтры с линейной ФЧХ и АЧХ с допустимыми пульсациями, причем уровень пульсаций зависит от частоты. Например, из рисунков 2.31 и 2.32 видно, что уровень пульсаций в полосе задерживания уменьшается по мере удаления от переходной полосы, однако при синтезе приходится ориентироваться на их максимальный уровень, который должен быть меньше допустимого. Поэтому возникает вопрос, нельзя ли уменьшить максимальный уровень за счет выравнивания пульсаций в пределах заданной полосы. Ответом на этот вопрос является метод наилучшей равномерной аппроксимации.
На рисунке 2.37 приведены требуемая АЧХ полосового фильтра D(θ), заданная в полосе пропускания и в полосе задерживания, и аппроксимирующая функция A(θ) с равновеликими пульсациями.
Точками обозначены экстремумы этой функции.
Рисунок 2.37 – Требуемая АЧХ D(θ) и функция A(θ) при
чебышевской аппроксимации