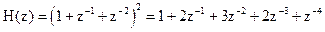.
Поскольку коэффициенты системной функции нерекурсивного фильтра являются отсчетами импульсной характеристики фильтра, то из полученного соотношения следует, что импульсная характеристика фильтра симметрична, а ее отсчеты сначала возрастают по линейному закону, а затем убывают также по линейному закону. Схема триангулярного фильтра четвертого порядка приведена на рисунке 2.25 а, а его импульсная характеристика на рисунке 2.25б. Из рисунка видно, что огибающая импульсной характеристики имеет форму равнобедренного треугольника, расположенного на пьедестале – прямоугольнике с высотой B0 и основанием 2N.
.
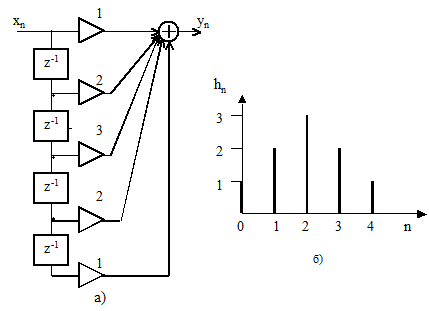
Рисунок 2.25– Триангулярный фильтр 4-го порядка
В общем случае триангулярный фильтр порядка 2N описывается следующим разностным уравнением
(2.23)
где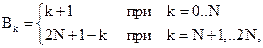 
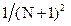-масштабный коэффициент на входе фильтра, при котором максимальный коэффициент передачи фильтра равен единице (на схеме рисунка 2.25а отсутствует).
Системная функция и комплексный коэффициент передачи этого фильтра определяются соотношениями:
, (2.24)
. (2.25)
На рисунках 2.26 и 2.27 приведены АЧХ и ФЧХ триангулярных фильтров второго и шестого порядков.
Рисунок 2.26 – АЧХ и ФЧХ триангулярного фильтра второго порядка (N=1)
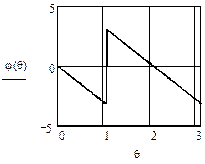
Рисунок 2.27 - АЧХ и ФЧХ триангулярного фильтра шестого порядка (N=3)
Сравнение этих характеристик с сответствующими характеристиками однородных фильтров показывает, что последовательное включение двух одинаковых однородных фильтров сужает полосу пропускания фильтра и уменьшает пульсации в полосе задерживания. ФЧХ триангулярного фильтра линейная или линейно-ломаная, как и ФЧХ однородного фильтра.
Лекция 7. Устойчивость цифровых фильтров
Тема 2. Цифровые фильтры
2.9. Устойчивость цифровых фильтров
Рассмотрим критерии устойчивости цифровых фильтров.
1.Критерий «ОВ-ОВ» («Ограниченный вход – ограниченный выход»)
Цифровой фильтр устойчив, если при ограниченном входном сигнале выходной сигнал фильтра также ограничен.
Условие ограниченности входного сигнала определяется соотношением 
, где 
, а условием ограниченности выходного сигнала является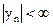 
.
Непосредственное использование этого критерия весьма затруднительно, т.к. требует определения значений отсчетов выходного сигнала при всех возможных значениях отсчетов входного сигнала. Поэтому требуются критерии, позволяющие оценить устойчивость фильтра на основании его характеристик.
2. Критерий оценки устойчивости по импульсной характеристике фильтра
В разделе 2.3 было доказано, что выходной сигнал фильтра представляет собой дискретную свертку входного сигнала и импульсной характеристики фильтра
.
Абсолютное значения отсчетов выходного сигнала удовлетворяет неравенству
.
При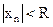 
справедливо неравенство
.
Следовательно,
.
Таким образом, чтобы обеспечить выполнение условия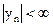 
, достаточно выполнить условие
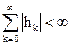. (2.28)
Последнее соотношение определяет критерий устойчивости цифрового фильтра, который формулируется так: цифровой фильтр устойчив, если сумма абсолютных значений отсчетов его импульсной характеристики конечна.
Из этого критерия следует, что все фильтры с конечной импульсной характеристикой абсолютно устойчивы.
В качестве примера воспользуемся критерием (2.28) для проверки устойчивости фильтра, импульсная характеристика которого бесконечна и описывается соотношением
,
где 
– положительная константа, от которой зависит скорость убывания отсчетов импульсной характеристики.
Учитывая, что 
, получим
.
Так как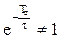 
, то фильтр устойчив.
3. Критерий оценки устойчивости по системной функции фильтра
В разделе 2.4 показано, что системная функция представляет собой Z-преобразование импульсной характеристики фильтра
.
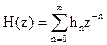Модуль системной функции удовлетворяет неравенству
.
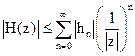При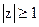 
справедливо неравенство
.
При 
и при 
модуль системной функции 
. Последнее соотношение означает, что в устойчивом цифровом фильтре должны отсутствовать полюсы системной функции в области комплексной переменной z, которая удовлетворяет неравенству 
.
Следовательно, если полюсы существуют, то в устойчивом фильтре они должны располагаться в области комплексной плоскости, для которой выполняется условие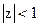 
.
Поэтому критерий устойчивости, связанный с системной функцией фильтра, формулируется следующим образом: цифровой фильтр устойчив, если полюсы системной функции располагаются внутри круга единичного радиуса с центром в начале координат ( ).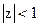
Оценим устойчивость фильтра, системная функция которого описывается соотношением
,
где A1= - 0.5.
Приравняем знаменатель системной функции нулю и определим корень полученного уравнения, который является координатой полюса
. 
Так как 
, то полюс системной функции располагается внутри круга единичного радиуса. Следовательно, фильтр устойчив.
2.10. Коэффициенты системной функции устойчивого звена
второго порядка
Системная функция звена второго порядка определяется соотношением
.
Для определения полюсов системной функции приравняем знаменатель нулю и найдем корни полученного квадратного уравнения
Фильтр реализуется в виде звеньев второго порядка в случае комплексно-сопряженных корней, т.е. при 
. (2.29)
В этом случае корни уравнения определяются следующим соотношением
.
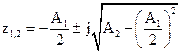Из последнего соотношения находим
.
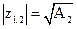Условием устойчивости звена является
.
Поэтому коэффициент A2 устойчивого звена второго порядка должен удовлетворять условию
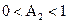. (2.30)
Из неравенств (2.29) и (3.30) следует неравенство для коэффициента A1
. (2.31)
Лекции 8 и 9. Синтез нерекурсивных цифровых фильтров
Тема №2. Цифровые фильтры
2.11. Нерекурсивный фильтр с линейной ФЧХ
На рисунке 2.28 показан нерекурсивный фильтр, у которого коэффициенты системной функции b симметричны относительно середины линии задержки.
Рисунок 2.28 – Нерекурсивный фильтр с линейной ФЧХ