 .
.
Весовая функция g(θ) определяется следующим образом

При g<1 пульсации АЧХ в полосе пропускания меньше, чем в полосе задерживания, а при g>1 наоборот. На рисунке 2.37 представлен случай, когда g = 1 и пульсации в полосе задерживания такие же, как в полосе пропускания.
Теорема о чебышевском альтернансе утверждает, что в случае оптимального решения ошибка имеет по крайней мере K+2 экстремума. Обозначим через  , где i= 0,1,..K+1, нормированные частоты экстремумов.
, где i= 0,1,..K+1, нормированные частоты экстремумов.
На этих частотах должно выполняться условие
 , где
, где 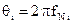 , i =0,1,..K+1
, i =0,1,..K+1
Приведенные соотношения представляют собой систему K+2 линейных уравнений с K+2 неизвестными, из которых K+1 неизвестная – коэффициенты Ck аппроксимирующей функции A(θ), а ещё одна неизвестная - ошибка  .
.
Трудность решения задачи состоит в том, что частоты чебышевского альтернанса  неизвестны.
неизвестны.
Поэтому сначала произвольно выбирают K+2 значения частот, решают приведенную систему уравнений, находят Ck и  и анализируют ошибку аппроксимации во всем интервале частот. Если в некоторых точках фактическая ошибка превосходит
и анализируют ошибку аппроксимации во всем интервале частот. Если в некоторых точках фактическая ошибка превосходит  , то выбирают новое множество экстремальных частот путем рассмотрения K+2 точек, где эта ошибка максимальна и имеет чередующийся знак.
, то выбирают новое множество экстремальных частот путем рассмотрения K+2 точек, где эта ошибка максимальна и имеет чередующийся знак.
В этой процедуре значение  на каждом шаге возрастает и, в конце концов, сходится к своей верхней границе.
на каждом шаге возрастает и, в конце концов, сходится к своей верхней границе.
Описанная итерационная процедура известна под названием второго алгоритма Ремеза. В соответствии с этим алгоритмом написана машинная программа, нашедшая широкое применение при расчете фильтров.
Лекция 10. Синтез рекурсивных цифровых фильтров
Тема 2. Цифровые фильтры
2.15. Синтез рекурсивных цифровых фильтров методом билинейного
Z – преобразования
Передаточная характеристика аналогового фильтра связана с импульсной характеристикой фильтра прямым преобразованием Лапласа
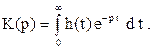
По аналогии с предыдущим соотношением дискретное преобразование Лапласа импульсной характеристики цифрового фильтра определяется выражением

В разделе 3.4 было показано, что системная функция цифрового фильтра представляет собой Z-преобразование импульсной характеристики фильтра

Из сопоставления двух последних соотношений следует, что для нахождения H(z) при известной передаточной характеристике аналогового фильтра-прототипа нужно сделать подстановку
 (2.34)
(2.34)
Передаточная характеристика аналогового фильтра-прототипа K(p) представляет собой дробно-рациональную функцию, у которой числитель и знаменатель выражаются полиномами относительно комплексной переменной p

Подстановка (2.34) не позволяет получить системную функцию в виде дробно-рациональной функции с полиномами относительно комплексной переменной z в числителе и знаменателе (2.7).
Чтобы найти системную функцию воспользуемся разложением ln(z) в ряд и ограничим количество членов этого ряда. Для этого сначала представим z в виде
 .
.
Найдем приближенное значение
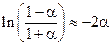 .
.
Выражая α через z и подставляя в последнее соотношение, получим
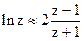 .
.
После подстановки последнего соотношения в (2.34) получим
 (2.35)
(2.35)
Это соотношение получило название билинейного Z- преобразования.
Докажем, что билинейное Z-преобразование преобразует устойчивый аналоговый фильтр в устойчивый цифровой фильтр. Для этого из последнего соотношения выразим z через p = s + jw, обозначив a = 2/TД

Откуда

Из этого соотношения видно, что при s<0 (условие устойчивости аналогового фильтра-прототипа)  (условие устойчивости цифрового фильтра). На рисунке 2.38 показаны затемненные области устойчивости аналогового фильтра – прототипа в плоскости p и цифрового фильтра в плоскости z.
(условие устойчивости цифрового фильтра). На рисунке 2.38 показаны затемненные области устойчивости аналогового фильтра – прототипа в плоскости p и цифрового фильтра в плоскости z.
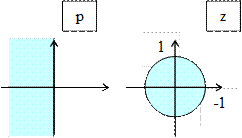
Рисунок 2.38 – Области устойчивости цифрового фильтра и аналогового прототипа
Таким образом, билинейное Z-преобразование преобразует левую полуплоскость плоскости p в круг единичного радиуса с центром в начале координат.
Найдем связь между цифровыми и аналоговыми частотами, на которых коэффициенты передачи цифрового фильтра и аналогового фильтра-прототипа одинаковы.
Используя билинейное Z – преобразование, можно выразить передаточную характеристику аналогового фильтра через системную функцию цифрового фильтра
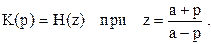
Следовательно, комплексный коэффициент передачи аналогового фильтра можно выразить через системную функцию цифрового фильтра

С другой стороны, комплексный коэффициент передачи цифрового фильтра связан с системной функцией следующим соотношением
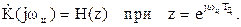
Из двух последних соотношений видно, что коэффициенты передачи цифрового фильтра и аналогового фильтра-прототипа равны при выполнении условия
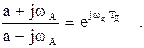
Преобразуя последнее соотношение, получим
 (2.36)
(2.36)
Таким образом, частота аналогового фильтра – прототипа связана с частотой цифрового фильтра при равенстве их комплексных коэффициентов передачи нелинейной зависимостью. Из рисунка 2.39 видно, что эта нелинейная зависимость вызывает сжатие АЧХ цифрового фильтра по сравнению с АЧХ аналогового фильтра – прототипа.

Рисунок 2.39 – АЧХ цифрового фильтра и аналогового фильтра – прототипа при
использовании билинейного Z – преобразования
Чтобы избежать сужения полосы пропускания цифрового фильтра аналоговый прототип рассчитывают, исходя не из граничных частот полосового фильтра, а из граничных аналоговых частот, определенных по (2.36) при подстановке в эту формулу граничных частот цифрового фильтра. При этом получают цифровой фильтр с требуемыми граничными частотами.
Из (2.36) следует также, что чем выше частота дискретизации, тем ближе частота аналогового фильтра – прототипа к частоте цифрового фильтра.
Если частота цифрового фильтра удовлетворяет условию 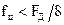 , то с погрешностью не более 5% можно считать аналоговую и цифровую частоты одинаковыми.
, то с погрешностью не более 5% можно считать аналоговую и цифровую частоты одинаковыми.
Заключение
Математическим аппаратом цифровой фильтрации является Z – преобразование. Знание трех основных свойств Z – преобразования (линейности, теоремы о задержки и о дискретной свертке) позволяет решать задачи анализа фильтра при известной схеме фильтра – графическом представлении алгоритма цифровой фильтрации.
Основные этапы анализа:
1. Выражение выходного сигнала фильтра через входной сигнал – запись разностного уравнения;
2. Выражение Z-преобразования выходного сигнала через Z – преобразование входного сигнала фильтра,
3. Определение системной функции фильтра  ;
;
4. Определение зависимости комплексного коэффициента передачи фильтра от частоты  путем использования подстановки в выражение системной функции
путем использования подстановки в выражение системной функции
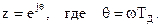
5. Определение АЧХ фильтра

6. Определение ФЧХ фильтра
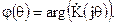
7. Определение импульсной характеристики фильтра путем нахождения обратного Z – преобразования системной функции фильтра.
Синтез цифровых фильтров состоит в определении коэффициентов системной функции фильтра при заданных требованиях к его АЧХ.
Важным достоинством нерекурсивных фильтров является линейность ФЧХ, поэтому все методы синтеза нерекурсивных фильтров предусматривают получение фильтра с линейной ФЧХ.
Наиболее простым из рассмотренных методов синтеза нерекурсивных фильтров является метод разложения функции, определяющей АЧХ фильтра, в ряд Фурье с последующим применением оконных функций.
Наиболее сложным с точки зрения программной реализации является метод равномерной чебышевской аппроксимации, но он обеспечивает минимальный уровень пульсаций АЧХ.
При синтезе рекурсивных фильтров чаще всего применяется метод билинейного Z – преобразования, который позволяет по известной передаточной характеристике аналогового фильтра-прототипа получить системную функцию цифрового фильтра.
Заключение
Математическим аппаратом цифровой фильтрации является Z – преобразование. Знание трех основных свойств Z – преобразования (линейности, теоремы о задержки и о дискретной свертке) позволяет решать задачи анализа фильтра при известной схеме фильтра – графическом представлении алгоритма цифровой фильтрации.
Основные этапы анализа:
8. Выражение выходного сигнала фильтра через входной сигнал – запись разностного уравнения;
9. Выражение Z-преобразования выходного сигнала через Z – преобразование входного сигнала фильтра,
10. Определение системной функции фильтра  ;
;
11. Определение зависимости комплексного коэффициента передачи фильтра от частоты  путем использования подстановки в выражение системной функции
путем использования подстановки в выражение системной функции
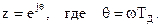
12. Определение АЧХ фильтра

13. Определение ФЧХ фильтра

14. Определение импульсной характеристики фильтра путем нахождения обратного Z – преобразования системной функции фильтра.
Контрольные вопросы по теме №2:
- Что такое импульсная характеристика цифрового фильтра?
- На рисунке 2.40 показаны входной сигнал фильтра xn и его импульсная характеристика hn. Начертите временную диаграмму выходного сигнала фильтра yn.

Рисунок 2.40
3. Определите 4 отсчета импульсной характеристики h0, h1, h2, h3 цифрового фильтра рисунка 2.41, где A = -0.5

Рисунок 2.41
4. Что называется системной функцией цифрового фильтра?
5. Определите системную функцию цифрового фильтра рисунка 2.41.
6. Какая связь существует между импульсной характеристикой и системной функцией цифрового фильтра?
7. Выразите Z-преобразование выходного сигнала цифрового фильтра рисунка 2.42 через Z –преобразование входного сигнала
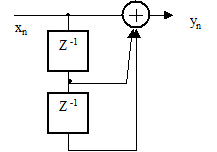
Рисунок 2.42
8. Выразите Z-преобразование выходного сигнала линии задержки рисунка 2.43 через Z-преобразование входного сигнала.

Рисунок 2.43
9. Выразите Z-преобразование выходного сигнала фильтра рисунка 2.44 через Z-преобразование входного сигнала.

Рисунок 2.44
10. На входе фильтра действует сигнал xn, а на выходе сигнал yn. Временные диаграммы этих сигналов приведены на рисунке 2.45. Определите системную функцию фильтра.
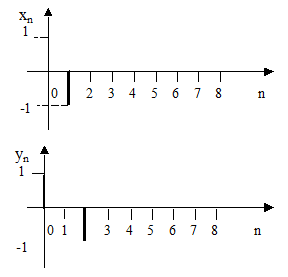
Рисунок 2.45
11. Системная функция цифрового фильтра определяется соотношением
 .
.
Чему равен полюс системной функции фильтра?
12. На рисунке 2.46 приведена импульсная характеристика цифрового фильтра. Какова системная функция фильтра?
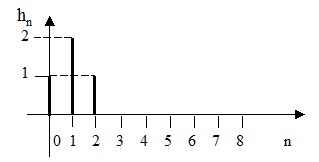
Рисунок 2.46
13. Какова системная функция цифрового фильтра рисунка 2.47
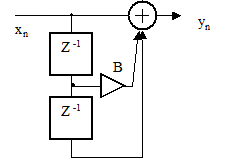
Рисунок 2.47
14. Системная функция цифрового фильтра определяется соотношением
 .
.
Чему равен нуль системной функции фильтра?
15. На входе фильтра (рисунок 2.48) действует сигнал xn (рисунок 2.49). Каков выходной сигнал фильтра при нулевых начальных условиях?


Рисунок 2.48 Рисунок 2.49
16. На рисунке 2.50 приведена импульсная характеристика цифрового фильтра. Выразите Z-преобразование выходного сигнала фильтра через Z-преобразование входного сигнала
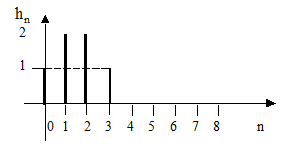
Рисунок 2.50
17. Каков коэффициент передачи фильтра (рисунок 2.51) на частоте, равной четверти частоты дискретизации?

Рисунок 2.51
18. Системная функция цифрового фильтра определяется соотношением
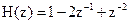 .
.
Чему равен коэффициент передачи фильтра на частоте f=0?
19. На входе цифровой линии задержки (рисунок 2.52) действует синусоидальный сигнал xn, частота которого равна одной восьмой частоты дискретизации. Чему равен фазовый сдвиг выходного сигнала yn относительно входного сигнал?
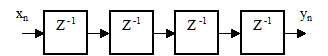
Рисунок 2.52
20. Какой из двух цифровых фильтров рисунка 2.53 обладает линейной ФЧХ?
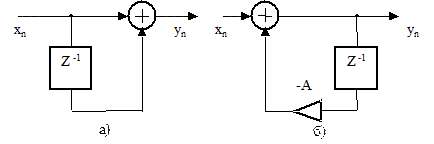
Рисунок 2.53
21. Системная функция цифрового фильтра определяется соотношением
 .
.
Чему равен фазовый сдвиг, вносимый фильтром на частоте, равной четверти частоты дискретизации?
22. На входе цифровой цепи рисунка 2.54 действует синусоидальный сигнал с амплитудой, равной единице. Чему равна амплитуда выходного сигнала?

Рисунок 2.54
23. Системная функция цифрового фильтра описывается соотношением
 .
.
Сделайте вывод об устойчивости фильтра.
24. Сделайте вывод об устойчивости фильтра рисунка 2.55 при A11= -0.5, A12= - 1.9.
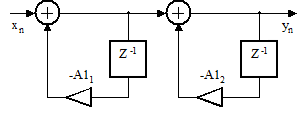
Рисунок 2.55
25. На рисунке 2.56 приведена импульсная характеристика цифрового фильтра. Сделайте заключение об устойчивости фильтра
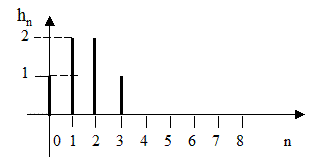
Рисунок 2.56
26. Системная функция цифрового фильтра описывается соотношением
 , где A1 = 0.1, А2 =0.9
, где A1 = 0.1, А2 =0.9
Сделайте вывод об устойчивости фильтра.
27. Системная функция цифрового фильтра определяется соотношением
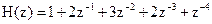 .
.
Сделайте вывод об устойчивости фильтра.
Контрольная карта ответов
Номер ответа соответствует номеру контрольного вопроса в предыдущем разделе.
2. 
3. y0 = 1.000, y1= 0.500, y2 = 0.250, y3 = 0.125.
5. 
7. 
8. 
9. 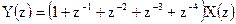
10. 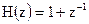
11. zп = 0.5
12. 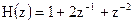
13. 
14. z0 = - 0.8
15. y0 = 1, y1 = 2, y2 =1
16. 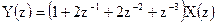
17. K=2
18. K=0
19. 
20. Рисунок 2.53 а
21. 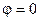
22. Амплитуда выходного сигнала Y=1
23. Не устойчив
24. Не устойчив
25. Устойчив
26. Устойчив
27. Устойчив
Список литературы по теме №2:
1. В.Г.Иванова, А.И.Тяжев. Цифровая обработка сигналов и сигнальные процессоры / Под редакцией д.т.н., профессора Тяжева А.И. - Самара, 2008г.
2.Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. –2-е изд., перераб. и доп.- СПб.: Политехника, 1999. –592с.:ил.
3.А.Б. Сергиенко. Цифровая обработка сигналов. – СПб.: Питер, 2002.-2002.-608с.:ил.
4.А.И. Солонина, Д.А. Улахович, С.М. Арбузов, Е.Б. Соловьёва. Основы цифровой обработки сигналов.- Изд. 2-е испр. И перераб. – СПб.: БХВ-Петербург, 2005.-768с.: ил.
5.Л. Рабинер, Б. Гоулд. Теория и применение цифровой обработки сигналов.- Издательство «Мир», 1978. –848с.,ил.
6.В. Каппелини, А.Дж.Константинидис, П.Эмилиани. Цифровые фильтры и их применение.- М.:Энергоатомиздат, 1983-360с.:ил.
7.Р.В. Хемминг. Цифровые фильтры. – М.: Сов. Радио, 1980-224с., ил.