I. Проверка устойчивости в плоскости рамы (XoZ):
Расчет на устойчивость внецентренно-сжатых элементов постоянного сечения в плоскости действия момента следует выполнять по формуле 109 [3]:
 (20)
(20)
В формуле (20) коэффициент устойчивости при внецентренном сжатии  следует определять по таблице Д.3 [3] в зависимости от условной гибкости
следует определять по таблице Д.3 [3] в зависимости от условной гибкости  и приведенного относительного эксцентриситета
и приведенного относительного эксцентриситета  , определяемого по формуле 110 [3]:
, определяемого по формуле 110 [3]:
 (21)
(21)
где 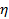 – коэффициент влияния формы сечения, определяемый по таблице Д.2 [3];
– коэффициент влияния формы сечения, определяемый по таблице Д.2 [3];
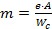 – относительный эксцентриситет,
– относительный эксцентриситет,
здесь  – эксцентриситет, при вычислении которого значения M и N следует принимать согласно требованиям п 9.2.3 [3];
– эксцентриситет, при вычислении которого значения M и N следует принимать согласно требованиям п 9.2.3 [3];
 – площадь поперечного сечения (приложение 3);
– площадь поперечного сечения (приложение 3);
 – момент сопротивления сечения, вычисленный для наиболее сжатого волокна (приложение 3)
– момент сопротивления сечения, вычисленный для наиболее сжатого волокна (приложение 3)
Условная гибкость определяется по следующей формуле:
 (22)
(22)
где  – расчетная длина надкрановой части, определяемая по формуле
– расчетная длина надкрановой части, определяемая по формуле  (
( - длина надкрановой части; коэффициент расчетной длины
- длина надкрановой части; коэффициент расчетной длины  определяется по приложению И [3]);
определяется по приложению И [3]);
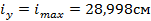 – максимальный радиус инерции (приложение 3);
– максимальный радиус инерции (приложение 3);
 – расчетное сопротивление стали С245 (приложение В, таблица В.5 [3]);
– расчетное сопротивление стали С245 (приложение В, таблица В.5 [3]);
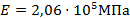 – модуль упругости стали (приложение Г, таблица Г.10 [3])
– модуль упругости стали (приложение Г, таблица Г.10 [3])

Рисунок 8 — Поперечное сечение надкрановой части колонны
Определим расчетную длину надкрановой части колонны  :
:
Коэффициент расчетной длины для верхнего участка одноступенчатой колонны следует определять по формуле И.5 [3]:
 (23)
(23)
Коэффициент расчетной длины  для защемленного в основании нижнего участка одноступенчатой колонны при закреплении верхнего конца от поворота, но при возможности его свободного смещения следует принимать по таблице И.4 [3] в зависимости от
для защемленного в основании нижнего участка одноступенчатой колонны при закреплении верхнего конца от поворота, но при возможности его свободного смещения следует принимать по таблице И.4 [3] в зависимости от  и
и  , определяемые по формулам (приложение И [3]):
, определяемые по формулам (приложение И [3]):
 (24)
(24)
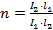 (25)
(25)
 (26)
(26)
где 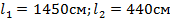 – длины нижнего и верхнего участков колонны (рис. 7);
– длины нижнего и верхнего участков колонны (рис. 7);
 – моменты инерции сечений нижнего и верхнего участка колонны (приложение 3);
– моменты инерции сечений нижнего и верхнего участка колонны (приложение 3);
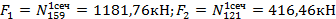 – продольные силы, приложенные к верху нижнего и верхнего участков колонн (рис. 7) определяемые по приложению 2
– продольные силы, приложенные к верху нижнего и верхнего участков колонн (рис. 7) определяемые по приложению 2


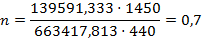
Так как  и
и  , то коэффициент расчетной длины подкрановой части колонны
, то коэффициент расчетной длины подкрановой части колонны  принимаем равным 1,675 (таблица И.4 [3]).
принимаем равным 1,675 (таблица И.4 [3]).
Коэффициент расчетной длины надкрановой части колонны:
 , значит принимаем
, значит принимаем 
Следовательно расчетная длина надкрановой части колонны составляет

Определим условную гибкость:

Определим приведенный относительный эксцентриситет  :
:
Продольную силу  и изгибающий момент
и изгибающий момент  принимаем из РСУ в 3 сечении для 121 элемента (приложение 2):
принимаем из РСУ в 3 сечении для 121 элемента (приложение 2):

Эксцентриситет: 
Относительный эксцентриситет: 
Определим коэффициент влияния формы сечения 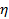 для 5 типа сечения по таблице Д.2 [3]:
для 5 типа сечения по таблице Д.2 [3]:
Так как  ,
,  и
и 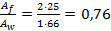 , то необходимо проинтерполировать:
, то необходимо проинтерполировать:


Применив интерполяцию, получаем 
Следовательно приведенный относительный эксцентриситет  будет равен:
будет равен:

Коэффициент устойчивости при внецентренном сжатии  определяем по таблице Д.3 [3]:
определяем по таблице Д.3 [3]:
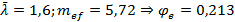
Проверка устойчивости в плоскости действия момента:

т.е. устойчивость в плоскости рамы обеспечена.
II. Проверка устойчивости из плоскости рамы (YoZ):
Расчет на устойчивость внецентренно-сжатых стержней сплошного постоянного сечения из плоскости действия момента следует выполнять по формуле 111 [3]:
 (27)
(27)
где  – коэффициент, определяемый согласно требованиям п 9.2.5 [3];
– коэффициент, определяемый согласно требованиям п 9.2.5 [3];
 – коэффициент устойчивости при центральном сжатии, определяемый по таблице Д.1 [3];
– коэффициент устойчивости при центральном сжатии, определяемый по таблице Д.1 [3];
 – коэффициент условий работы [3]
– коэффициент условий работы [3]
Определим относительный эксцентриситет  по формуле п 8.4.1 [3]:
по формуле п 8.4.1 [3]:
 (28)
(28)
где  – максимальный момент в пределах средней трети длины надкрановой части колонны, но не менее половины наибольшего момента по длине стержня (рис. 9);
– максимальный момент в пределах средней трети длины надкрановой части колонны, но не менее половины наибольшего момента по длине стержня (рис. 9);

Рисунок 9 — Эпюра моментов 

Так как  , то коэффициент
, то коэффициент  определяется по формуле 112 [3]:
определяется по формуле 112 [3]:
 (29)
(29)
где  – коэффициенты, определяемые по таблице 21 [3]
– коэффициенты, определяемые по таблице 21 [3]
Коэффициент  для 1 типа сечения при
для 1 типа сечения при  определяется по формуле:
определяется по формуле:
 (30)
(30)
Для определения коэффициента  необходимо определить условную гибкость
необходимо определить условную гибкость  :
:
 (31)
(31)
где  – расчетная длина надкрановой части из плоскости рамы;
– расчетная длина надкрановой части из плоскости рамы;
 – минимальный радиус инерции (приложение 3);
– минимальный радиус инерции (приложение 3);
Коэффициент  для 1 типа сечения при
для 1 типа сечения при  равен 1.
равен 1.
 - условие выполняется
- условие выполняется
Определим коэффициент устойчивости  при центральном сжатии по таблице Д.1 [3]:
при центральном сжатии по таблице Д.1 [3]:
Для типа сечения  и при
и при  коэффициент устойчивости
коэффициент устойчивости  равен 0,703.
равен 0,703.
Проверка устойчивости из плоскости действия момента:

т.е. устойчивость из плоскости рамы обеспечена.
III. Проверка местной устойчивости стенки:
Устойчивость стенок следует считать обеспеченной, если условная гибкость стенки  не превышает значений предельной условной гибкости
не превышает значений предельной условной гибкости  (п 9.4.2 [3]):
(п 9.4.2 [3]):
 (32)
(32)
Предельная условная гибкость  определяется по формулам таблицы 22 [3]:
определяется по формулам таблицы 22 [3]:
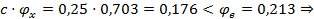 тип сечения — 2.
тип сечения — 2.
Определим коэффициент  по формуле (таблица 22 [3]):
по формуле (таблица 22 [3]):
 (33)
(33)
где  – наибольшее сжимающее напряжение у расчетной границы стенки;
– наибольшее сжимающее напряжение у расчетной границы стенки;
 – соответствующее напряжение у противоположной расчетной границы стенки
– соответствующее напряжение у противоположной расчетной границы стенки
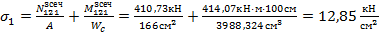 (34)
(34)
 (35)
(35)

Для сечения типа 2 при  значения
значения  следует определять дважды: согласно таблицы 9 и таблицы 22 [3]:
следует определять дважды: согласно таблицы 9 и таблицы 22 [3]:
1) Определим  по таблица 9 [3]:
по таблица 9 [3]:
 , следовательно используем формулу 24 [3]
, следовательно используем формулу 24 [3]
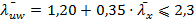 (36)
(36)
 - условие выполняется
- условие выполняется
2) Определим  по таблица 22 [3]:
по таблица 22 [3]:
 , следовательно используем формулу 125 [3]
, следовательно используем формулу 125 [3]
 (37)
(37)

Проверка местной устойчивости стенки:

т.е. местная устойчивость стенки не обеспечена.
Укрепляем стенку продольными ребрами жесткости с размерами (п 7.3.3 [3]):
- ширина выступающей части для парного симметричного ребра:
 (38)
(38)
Принимаем 
- толщина ребра должна быть:
 (39)
(39)
Принимаем 
IV. Проверка местной устойчивости полок:
Устойчивость полок следует считать обеспеченной, если условная гибкость полки  не превышает значений предельной условной гибкости
не превышает значений предельной условной гибкости  (п 9.4.7 [3]):
(п 9.4.7 [3]):
 (40)
(40)
Предельная условная гибкость  определяется по формуле 132 таблицы 23 [3]:
определяется по формуле 132 таблицы 23 [3]:
 (41)
(41)

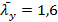
Предельная условная гибкость свеса полки 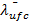 определяется по формуле 37 таблицы 10 [3]:
определяется по формуле 37 таблицы 10 [3]:
 (42)
(42)



Проверка местной устойчивости полки:

т.е. местная устойчивость стенки обеспечена.