ТАБЛИЦЫ ЗНАЧЕНИЙ ФУНКЦИЙ И ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ

Варианты заданий:

1. Имеются следующие данные измерения температуры воздуха в продолжении дня:

8час-7 10час-10 13час-15

14час-15 17час-9 20час-8

Определить, какой температура воздуха была в 9 час, в 12 час.30мин., в 15час.15мин. Проверить результат вычисления по графику.

2. Используя данные задачи1, определить в какое время температура была равна 9,12, 14.5. Задачу решить с помощью графика.

3. Таблица значений некоторой функции имеет постоянный шаг и задана числами a,b,y1,….,y50. С помощью алгоритма интерполяции такую таблицу этой же функции, которая имеет шаг π/3.

4. Дана таблица некоторой функции. Шаг таблицы не является постоянным. Используя рассмотренный алгоритм, получить для этой функции таблицу с постоянным шагом. Число значений функции задается пользователем.

5. Применить алгоритм интерполяции к таблице значений некоторой известной функции (например, sinx или х²). Сравнить результаты интерполяции со значением функции.

6. Рассмотрим один из методов приближенного интегрирования – алгоритм трапеции. Отрезок [a,b] разбивается на n равных частей точками xi, i=1,n+1. Площадь каждой полосы между прямыми x=xr и x=xr+1 приближенно вычисляется как площадь трапеции, ограниченной этими прямыми, осью абсцисс и хордой, соединяющей точки с координатами (Xr,f(Xr);(Xr+1,f(Xr+1)). Такая трапеция имеет площадь: .

Сумма этих площадей . Введем обозначение , тогда формула приближенного интегрирования имеет вид:

Вычислить по данному алгоритму .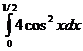

7. По рассмотренному в задании 6 алгоритму вычислить интеграл: .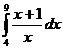

8. Часто пытаются статистические данные уложить в простую формулу. Пусть имеется несколько точек Xi, i=1,n, в которых проводились испытания. Результаты испытаний – это значения Yi(i=1,n). По этим данным строят точечный график функции и предполагают вид зависимости Y от Х (линейная, квадратная и т.п.). Назовем эту зависимость Y(x) и будем считать, что получается линейная зависимость, т.е. Y(x)=rx+b. Остается определить значения коэффициентов r и b. Их берут такими, что величина (Y1-Rx1-b)²+(Y2-Rx2-b)²+…+(Yn-Rxn-b)² имеет наименьшее значение. Как показал Гаусс, выписанная сумма квадратов имеет наименьшее значение при следующих r и b.

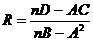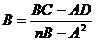, , где А=Х1+…+Хn, С=Y1+…+Yn, B=X1²+…+Xn², D=X1Y1+…+XnYn.

Этот алгоритм получения коэффициентов линейной зависимости величины Y от X называется алгоритмом наименьших квадратов. Пусть при экспериментальном исследовании установлено, что для х=1,5 значения Y равны 4.5, 7, 9, 12, 13. На основе этих данных вывести линейный закон Y(x) решить задачу по алгоритму и путем подбора и сравнить результаты. Подбор сделать графически.

9. Пользуясь методом наименьших квадратов (см.зад.8) определить линейную зависимость количества растворяющегося вещества в зависимости от температуры, если известны следующие данные:

Температура: 0, 4, 10, 15, 21, 29, 56, 51, 68.

Кол.вещества: 66.7, 71, 76.3, 80.6, 85.7, 92.9, 99.4, 116.6, 125.1

10. Написать программу, в результате выполнения которой по данным Х1, …Хn, Y1,…Yn вычисляются коэффициенты в соответствии с алгоритмом наименьших квадратов (см.зад.8). После этого вычисления рассматриваются значения аргумента, поочередно вводимые с клавиатуры и для каждого из них вычисляется значение линейной функции.

11. Написать уравнение прямой проходящей через точки с координатами (1,1) и (1.5, 1.8)

12. Написать программу которая для значений t, выходящих за границы отрезка [ x1,xn] тоже находила бы осмысленный ответ: если t<x1, то для определения ответа может использоваться прямая, проходящая через [x1, y1] и [x2,y2],если t.xn, то прямая прошодящая через точки [xn-1, yn-1] и [xn, yn]. Шаг таблицы взять постоянным.

13. Решить задачу №12 для таблицы с непостоянным шагом.

14.,15. Пусть функция y=f(x),график которой является непрерывной линией принимает при x=a и x=b значения разных знаков: f(a)f(b)<0.Корню уравнения f(x)=0 соответствует точка пересечения графика функции y=f(x) с осью абцисс. В качестве приближения к корню, принадлежащему отрезку [a, b] можно взять точку ‘c’ пересечения прямой проходящей через точки с координатами (a, f(a)), (b, f(b)), с осью абцисс.Далее можно перейти к поиску корня на отрезке [ a, c] или на отрезке [c, b] в зависимости от знака f(c).Вотличие от алгоритма деления отрезка попалам этот процесс не всегда приводит к неограниченному уменьшению отрезка.Поэтому в качестве условия, при выполнении которого завершается процесс вычисления корня, здесь обычно берется |f(c)|<e, где e-данное малое положительное число.Уравнением прямой проходящей через точки с координатами (a, f(a)), (b, f(b)) будет y=((f(b)-f(a))/(b-a))*(x-a)+f(a).Решением уравнения =((f(b)-f(a))/(b-a))*(x-a)+f(a)=0, будет a=((b-a)/(f(b)-f(a))*f(a), именно это значение соответствует точке с. Этот алгоритм приближенного решения уравнения называется методом хорд. Довольно часто этот алгоритм требует меньших вычислений,чем алгоритм деления отрезка пополам.

Методом хорд решить уравнения: