Метод 1.
Расчет детальным методом по схеме плоской задачи в координатах (x; z).
В реку Бирюса сбрасываются сточные воды Бирюсинского гидролизного завода. В створе, расположенном в 4,5 км ниже сброса сточных вод наблюдается превышение ПДК по фенолу, вычислим, через какое расстояние, концентрация загрязняющего вещества будет ниже ПДК.
Данные за 28.04.98
Qp = 266 м3/с
Vcp = 0,66 м/с
Qcт = 0,23 м3/с
Н = 2,99 м
В = 167 м
Сст = 0,013 г/м3 = 13 мкг/л
Ср = 0 г/м3
I = 0.23 0/00
ПДК (фенолы) = 0,001 мг/л
Определим площадь струи начальном сечении:
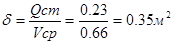
Определим ширину загрязненной части в начальном створе:

Предположим, что размер расчетной клетки равен Δz = 0,02 м, тогда количество клеток, расположенных в зоне загрязнения равно b/Δz=0.12/0.02 = 6 клеток.
Рассчитаем коэффициент Шези по формуле:
 м1/2/с
м1/2/с
Найдем функцию коэффициента Шези:
M = 0,7 • Cш + 6 =0,7 · 25,1 + 6 = 23,57
Рассчитаем коэффициент турбулентной диффузии
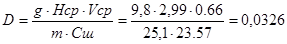 м2/с
м2/с
Определим, через какой промежуток устанавливать следующий створ:

7. Находим концентрацию загрязняющего вещества в каждом створе через промежуток 0,4 метра. Строим поле концентрации фенола:
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,00 | 0,02 | 0,01 | 0,02 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,00 | 0,01 | 0,01 | 0,03 | 0,02 | 0,04 | 0,02 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,03 | 0,01 | 0,04 | 0,03 | 0,06 | 0,04 | 0,08 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,00 | 0,02 | 0,01 | 0,04 | 0,03 | 0,07 | 0,04 | 0,10 | 0,06 | 0,13 | 0,08 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,02 | 0,01 | 0,04 | 0,02 | 0,08 | 0,04 | 0,11 | 0,07 | 0,15 | 0,10 | 0, 19 | 0,13 | 0,23 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,03 | 0,02 | 0,08 | 0,04 | 0,13 | 0,08 | 0,18 | 0,11 | 0,24 | 0,15 | 0,29 | 0, 19 | 0,33 | 0,23 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,06 | 0,03 | 0,14 | 0,08 | 0,22 | 0,13 | 0,29 | 0,18 | 0,36 | 0,24 | 0,42 | 0,29 | 0,48 | 0,33 | 0,53 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,13 | 0,06 | 0,25 | 0,14 | 0,36 | 0,22 | 0,45 | 0,29 | 0,53 | 0,36 | 0,60 | 0,42 | 0,66 | 0,48 | 0,72 | 0,53 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,25 | 0,13 | 0,44 | 0,25 | 0,58 | 0,36 | 0,69 | 0,45 | 0,78 | 0,53 | 0,85 | 0,60 | 0,91 | 0,66 | 0,96 | 0,72 | 1,01 |
| 0,00 | 0,00 | 0,00 | 0,50 | 0,25 | 0,75 | 0,44 | 0,91 | 0,58 | 1,02 | 0,69 | 1,10 | 0,78 | 1,16 | 0,85 | 1,21 | 0,91 | 1,26 | 0,96 | 1,29 | 1,01 |
| 0,00 | 0,00 | 1,00 | 0,50 | 1,25 | 0,75 | 1,38 | 0,91 | 1,45 | 1,02 | 1,51 | 1,10 | 1,55 | 1,16 | 1,58 | 1,21 | 1,61 | 1,26 | 1,63 | 1,29 | 1,64 |
| 0,00 | 2,00 | 1,00 | 2,00 | 1,25 | 2,00 | 1,38 | 2,00 | 1,45 | 2,00 | 1,51 | 2,00 | 1,55 | 2,00 | 1,58 | 2,00 | 1,61 | 2,00 | 1,63 | 1,99 | 1,64 |
| 4,00 | 2,00 | 3,00 | 2,00 | 2,75 | 2,00 | 2,63 | 2,00 | 2,55 | 2,00 | 2,49 | 2,00 | 2,45 | 2,00 | 2,42 | 2,00 | 2,38 | 2,00 | 2,36 | 1,99 | 2,33 |
| 4,00 | 4,00 | 3,00 | 3,50 | 2,75 | 3,25 | 2,63 | 3,09 | 2,55 | 2,98 | 2,49 | 2,90 | 2,45 | 2,83 | 2,42 | 2,77 | 2,38 | 2,72 | 2,36 | 2,67 | 2,33 |
| 4,00 | 4,00 | 4,00 | 3,50 | 3,75 | 3,25 | 3,56 | 3,09 | 3,42 | 2,98 | 3,31 | 2,90 | 3,21 | 2,83 | 3,13 | 2,77 | 3,05 | 2,72 | 2,98 | 2,67 | 2,91 |
| 4,00 | 4,00 | 4,00 | 4,00 | 3,75 | 3,88 | 3,56 | 3,75 | 3,42 | 3,63 | 3,31 | 3,52 | 3,21 | 3,42 | 3,13 | 3,33 | 3,05 | 3,24 | 2,98 | 3,15 | 2,91 |
| 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 3,88 | 3,94 | 3,75 | 3,84 | 3,63 | 3,74 | 3,52 | 3,63 | 3,42 | 3,53 | 3,33 | 3,43 | 3,24 | 3,33 | 3,15 | 3,24 |
| 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 4,00 | 3,94 | 3,94 | 3,84 | 3,84 | 3,74 | 3,74 | 3,63 | 3,63 | 3,53 | 3,53 | 3,43 | 3,43 | 3,33 | 3,33 | 3,24 |
| 0,4 | 0,8 | 1,2 | 1,6 | 2,4 | 2,8 | 3,2 | 3,6 | 4,4 | 4,8 | 5,2 | 5,6 | 6,4 | 6,8 | 7,2 | 7,6 |
Так как загрязняющее вещество оказалось больше, чем в 20 клетках, то клетки можно объединить по формуле:
∆Xукр=∆Xпред•m2
где m - количество клеток, которые мы собираемся объединять в одну.
Рассчитаем новое расстояние между створами:
∆Xукр=0,4 · 22 = 1,6 м
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 | 0,02 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,03 | 0,04 | 0,04 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,03 | 0,04 | 0,05 | 0,05 | 0,06 | 0,07 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,04 | 0,05 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 | 0,10 | 0,11 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,08 | 0,09 | 0,10 | 0,11 | 0,12 | 0,13 | 0,15 | 0,16 | 0,17 |
| 0,00 | 0,01 | 0,01 | 0,01 | 0,02 | 0,03 | 0,04 | 0,06 | 0,07 | 0,09 | 0,10 | 0,12 | 0,13 | 0,15 | 0,17 | 0,18 | 0, 20 | 0,21 | 0,23 | 0,24 | 0,25 |
| 0,01 | 0,01 | 0,03 | 0,04 | 0,06 | 0,07 | 0,10 | 0,12 | 0,14 | 0,16 | 0,18 | 0, 20 | 0,23 | 0,25 | 0,27 | 0,28 | 0,30 | 0,32 | 0,34 | 0,35 | 0,37 |
| 0,02 | 0,05 | 0,07 | 0,10 | 0,13 | 0,16 | 0, 19 | 0,22 | 0,25 | 0,28 | 0,31 | 0,33 | 0,36 | 0,38 | 0,40 | 0,42 | 0,44 | 0,46 | 0,48 | 0,49 | 0,50 |
| 0,08 | 0,13 | 0,18 | 0,22 | 0,27 | 0,31 | 0,35 | 0,39 | 0,42 | 0,45 | 0,48 | 0,51 | 0,54 | 0,56 | 0,58 | 0,60 | 0,62 | 0,63 | 0,65 | 0,66 | 0,67 |
| 0,23 | 0,31 | 0,37 | 0,44 | 0,49 | 0,54 | 0,58 | 0,62 | 0,66 | 0,69 | 0,71 | 0,74 | 0,76 | 0,78 | 0,79 | 0,81 | 0,82 | 0,83 | 0,84 | 0,85 | 0,86 |
| 0,53 | 0,62 | 0,70 | 0,76 | 0,81 | 0,86 | 0,89 | 0,92 | 0,95 | 0,97 | 0,99 | 1,01 | 1,02 | 1,03 | 1,04 | 1,05 | 1,05 | 1,05 | 1,06 | 1,06 | 1,06 |
| 1,01 | 1,09 | 1,15 | 1, 19 | 1,22 | 1,25 | 1,27 | 1,28 | 1,29 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,30 | 1,29 | 1,29 | 1,28 | 1,28 | 1,27 | 1,26 |
| 1,64 | 1,67 | 1,68 | 1,69 | 1,68 | 1,68 | 1,67 | 1,66 | 1,64 | 1,63 | 1,61 | 1,60 | 1,58 | 1,56 | 1,55 | 1,53 | 1,51 | 1,50 | 1,48 | 1,47 | 1,45 |
| 2,33 | 2,28 | 2,23 | 2,18 | 2,13 | 2,09 | 2,04 | 2,00 | 1,96 | 1,93 | 1,89 | 1,86 | 1,82 | 1,79 | 1,76 | 1,74 | 1,71 | 1,68 | 1,66 | 1,63 | 1,61 |
| 2,91 | 2,79 | 2,68 | 2,58 | 2,49 | 2,41 | 2,34 | 2,27 | 2,21 | 2,16 | 2,10 | 2,05 | 2,01 | 1,97 | 1,93 | 1,89 | 1,85 | 1,82 | 1,79 | 1,76 | 1,73 |
| 3,24 | 3,08 | 2,93 | 2,80 | 2,69 | 2,59 | 2,50 | 2,42 | 2,35 | 2,28 | 2,22 | 2,16 | 2,11 | 2,06 | 2,01 | 1,97 | 1,93 | 1,89 | 1,85 | 1,82 | 1,79 |
| 9,6 | 11,2 | 12,8 | 14,4 | 17,6 | 19,2 | 20,8 | 22,4 | 25,6 | 27,2 | 28,8 | 30,4 | 33,6 | 35,2 | 36,8 | 38,4 |
Снова укрупним клетки
∆Xукр=1,6 · 22 = 6,4 м
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,01 | 0,02 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 | 0,02 | 0,02 | 0,03 | 0,03 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,02 | 0,04 | 0,03 | 0,05 | 0,04 | 0,06 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,01 | 0,01 | 0,02 | 0,02 | 0,03 | 0,03 | 0,04 | 0,04 | 0,06 | 0,05 | 0,07 | 0,06 | 0,08 | 0,08 |
| 0,00 | 0,00 | 0,00 | 0,01 | 0,02 | 0,03 | 0,03 | 0,05 | 0,05 | 0,07 | 0,06 | 0,09 | 0,08 | 0,10 | 0,09 | 0,12 | 0,11 | 0,14 |
| 0,00 | 0,01 | 0,02 | 0,03 | 0,06 | 0,05 | 0,08 | 0,07 | 0,11 | 0,09 | 0,13 | 0,12 | 0,15 | 0,14 | 0,17 | 0,16 | 0, 19 | 0,17 |
| 0,01 | 0,05 | 0,06 | 0,10 | 0,09 | 0,14 | 0,12 | 0,17 | 0,14 | 0, 19 | 0,17 | 0,22 | 0, 20 | 0,24 | 0,22 | 0,26 | 0,24 | 0,28 |
| 0,09 | 0,12 | 0,18 | 0,15 | 0,21 | 0,18 | 0,25 | 0,22 | 0,28 | 0,25 | 0,31 | 0,27 | 0,33 | 0,30 | 0,35 | 0,32 | 0,37 | 0,33 |
| 0,23 | 0,31 | 0,23 | 0,33 | 0,27 | 0,36 | 0,31 | 0,39 | 0,35 | 0,42 | 0,38 | 0,44 | 0,40 | 0,46 | 0,42 | 0,47 | 0,43 | 0,48 |
| 0,53 | 0,34 | 0,48 | 0,40 | 0,51 | 0,45 | 0,54 | 0,48 | 0,56 | 0,51 | 0,58 | 0,53 | 0,59 | 0,54 | 0,59 | 0,55 | 0,59 | 0,55 |
| 0,44 | 0,65 | 0,57 | 0,69 | 0,62 | 0,71 | 0,65 | 0,73 | 0,67 | 0,73 | 0,68 | 0,73 | 0,68 | 0,73 | 0,68 | 0,72 | 0,67 | 0,71 |
| 0,77 | 0,80 | 0,90 | 0,85 | 0,92 | 0,86 | 0,92 | 0,85 | 0,90 | 0,84 | 0,88 | 0,83 | 0,87 | 0,81 | 0,85 | 0,80 | 0,83 | 0,78 |
| 1,16 | 1,15 | 1,13 | 1,15 | 1,10 | 1,12 | 1,06 | 1,08 | 1,02 | 1,04 | 0,98 | 1,00 | 0,95 | 0,97 | 0,92 | 0,94 | 0,89 | 0,91 |
| 1,53 | 1,46 | 1,40 | 1,34 | 1,31 | 1,25 | 1,24 | 1,18 | 1,17 | 1,12 | 1,12 | 1,07 | 1,07 | 1,03 | 1,03 | 0,99 | 0,99 | 0,96 |
| 1,76 | 1,65 | 1,55 | 1,48 | 1,41 | 1,36 | 1,31 | 1,27 | 1,23 | 1, 20 | 1,16 | 1,14 | 1,11 | 1,09 | 1,06 | 1,04 | 1,02 | 1,00 |
| 46,4 | 49,6 | 51,2 | 52,8 | 54,4 | 57,6 | 59,2 | 60,8 | 62,4 | 65,6 | 67,2 | 68,8 | 70,4 |
Ответ: на расстоянии 72 метров концентрация фенолов достигнет уровня ПДК и станет равной 1 мкг/л
Метод 2.
Экспресс-метод ГГИ
Для сравнения определим расстояние до места, на котором концентрация загрязняющего вещества не превышает ПДК другим методом.
Условие то же, а именно: в реку Бирюса сбрасываются сточные воды Бирюсинского гидролизного завода. В створе, расположенном в 4,5 км ниже сброса сточных вод наблюдается превышение ПДК по фенолу, вычислим, через какое расстояние, концентрация загрязняющего вещества будет ниже ПДК.
Данные за 28.04.98
Qp = 266 м3/с
Vcp = 0,66 м/с
Qcт = 0,23 м3/с
Н = 2,99 м
В = 167 м
Сст = 0,013 г/м3 = 4 мкг/л
Ср = 0 г/м3
Сш = 25,1 м1/2/с
М = 23,57
ПДК (фенолы) = 0,001 мг/л = 1 мкг/л
Найдем отношение глубины реки к ее ширине:
 =H/B=2,99/167=0.0179
=H/B=2,99/167=0.0179
Найдем безразмерную величину, характеризующую турбулентный поток.

3. Найдем концентрацию загрязняющего вещества в потоке:
 мг/л
мг/л
4. Зная, что величина χ рассчитывается по формулам:

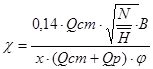
определим расстояние от места сброса сточных вод, на котором концентрация загрязняющего вещества не будут превышать ПДК, которое равно 1 мкг⁄л.
 м.
м.
Ответ: Концентрация ПДК достигнет уровня ПДК на расстоянии 4,2 метра.
Сравнительная оценка полученных результатов расчетов:
Результаты расчетов по детальному методу и экспресс-методу ГГИ довольно сильно различаются, хотя теоретически они должны быть одинаковы. Это можно попытаться объяснить несколькими причинами. Во-первых, вполне вероятна ошибка в расчетах, во-вторых довольно большую погрешность может давать большая разница объеме сточных вод и расходе реки. Далее, в первом методе поле концентрации строится по длине и ширине реки, не учитывая глубину. Может быть, еще одной причиной является то, что все-таки второй метод и называется экспресс-методом, т.е. он позволяет быстро определить концентрацию вещества на любом расстоянии, не учитывая многих параметров.
Все-таки довольно большая разница в окончательных цифрах представляется мне довольно странной. К сожалению, проверить точность расчетов другими методами не представляется возможным поскольку расчет детальным методом по схеме пространственной задачи затруднен тем, что при расчетах размер клетки получается очень маленький, и, следовательно, количество слоев по глубине получается очень большое. Расчет общего разбавления детальным методом с учетом начального разбавления также невозможен по причине того, что сброс сточных вод в нашем случае осуществляется с берега, а не в середину живого сечения. Комбинированный метод затруднен тем, что мы не знаем некоторых начальных данных, таких как среднее значение абсолютной величины поперечной составляющей скорости на вертикали и максимальную глубину на данном участке реки.